Binary Search Tree

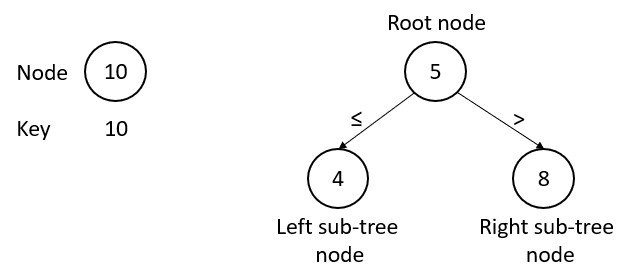
Basically, a binary search tree is just a rooted binary tree in which all nodes are arranged in an order.

In this case, nodes with keys equal to or less than the root node are located on the left sub-tree, whereas those with keys greater than the root are stored on the right sub-tree.

Binary Search Tree was invented by P.F. Windley, A.D. Booth, A.J.T. Colin, and T.N. Hibbard in 1960.

1. The nodes are connected together by a linked list data structure.

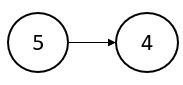
2. Each node has three associated nodes, Parent, left child, and right child. The root node has no parent node.

3. If a parent node or child node is missing, then the associated node value is NIL. The root node has a parent value of NIL.

4. The basic operations of binary search tree (BST) has

• In-order tree walk
• Search
• Minimum
• Maximum
• Successor
• Predecessor
• Insert
• Delete

5. The time required to perform basic operations (not in-order tree walk) is proportional to the height h of the tree, O(h).

6. For a binary search tree with n nodes, the height of the tree is log n.

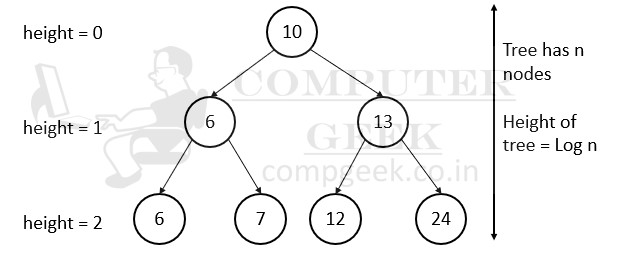
If tree is a linear array, then it would cost us O(n) time in worst case.

7. BST can be used as a dictionary because when in searching, we know where the target node is by looking at the root. It will take log n time to search the targeted node.

.

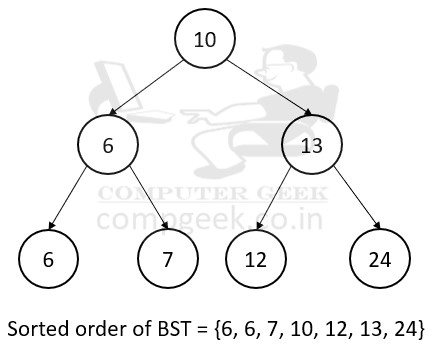
(i) In-order tree walk –

Print the nodes of BST in sorted order.

We print the nodes of BST in sorted order by in-order tree walk. It is a recursive algorithm.

Algorithm

In-ordertreewalk(n)

1. if n is not equal to NIL.
2. In-ordertreewalk(left(n))
3. print n;
4. In-ordertreewalk(right(n))

Time Complexity is O(n) because it travels all the nodes in the BST.

.

(ii) Search –

If you wish to search a key in a binary search tree, you need an algorithm that finds the left subtree if the key is less than or equal to node n and finds the right subtree if the key is greater than node n.

Example – if you want to search 12 in the binary search tree.

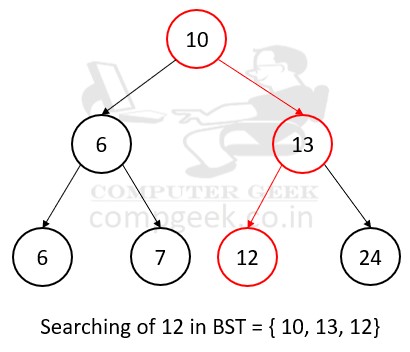
Algorithm

SearchingBST(n, key)

1. traverse the root node
2. if n = NIL or key = n
3. print it.
4. If root ≤ key
5. search the left subtree
6. else
7. search the right subtree

Time Complexity of searching a binary search tree is O(h).

However, in other cases,

-> Worst-case time complexity = O(n) = O(h) where h is the height of tree. This case happens because we find the time in a skewed tree.

-> Best-case time complexity = O(1). Root is search key.

.

(iii) Minimum

If you want to search the minimum key inside the binary search tree, then you have to search the node on the far left. The key is the smallest among all keys in binary search tree.

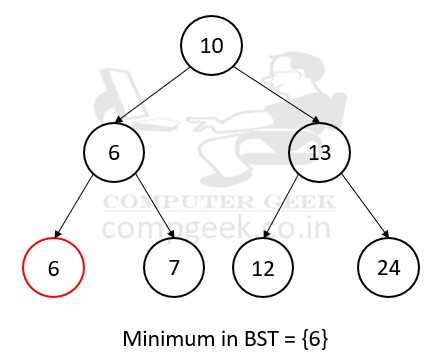
Algorithm

MinimumBST(n,min)

1. while (key ≠ NIL)
2. do left(n)

Time complexity of finding the minimum in binary search tree is O(h).

However, in other cases

-> Best-case time complexity is O(1). Root has no left subtree.

-> Worst-case time complexity is O(n). Left skewed tree has to traverse all the nodes to find the minimum.

.

(iv) Maximum

If you want to search the maximum key inside the binary search tree, then you have to search the node on the far right. The key is the largest among all keys in binary search tree.

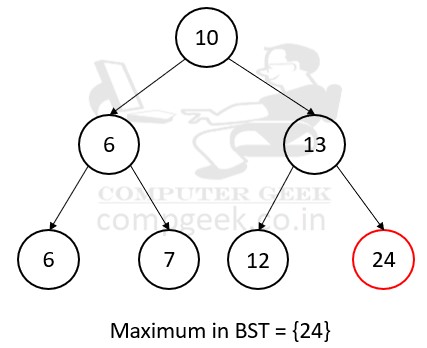
Algorithm

MaximumBST(n,max)

1. while (key ≠ NIL)
2. do right(n)

Time complexity of finding the maximum in binary search tree is O(h).

However, in other cases

-> Best-case time complexity is O(1). Root has no right subtree.

-> Worst-case time complexity is O(n). Right skewed tree has to traverse all the nodes to find the maximum.

.

(v) Successor

When traversing a binary search tree in sorted order, the successor of a node is the next node (right adjacent) to it.

Alternately, we may state that, assuming all of the keys are unique, the successor of key n is the node with the lowest key larger than key n.

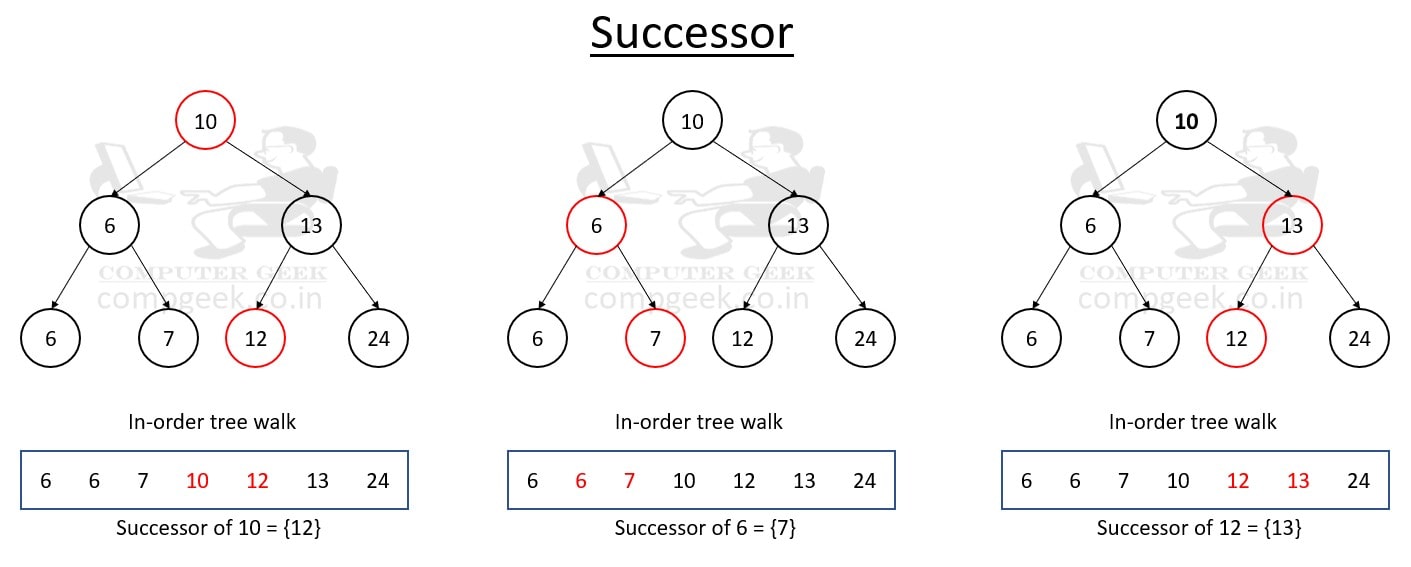
Algorithm

Successor(n)

1. Pick the right subtree of n.
2. Successor <- Minimum of right subtree
3. If right child is not present
4. then look for the parent of n.
5. if n is left child of parent
6. then Successor <- parent.
7. Else, successor = NIL.

Time complexity of finding the successor in binary search tree is O(h).

.

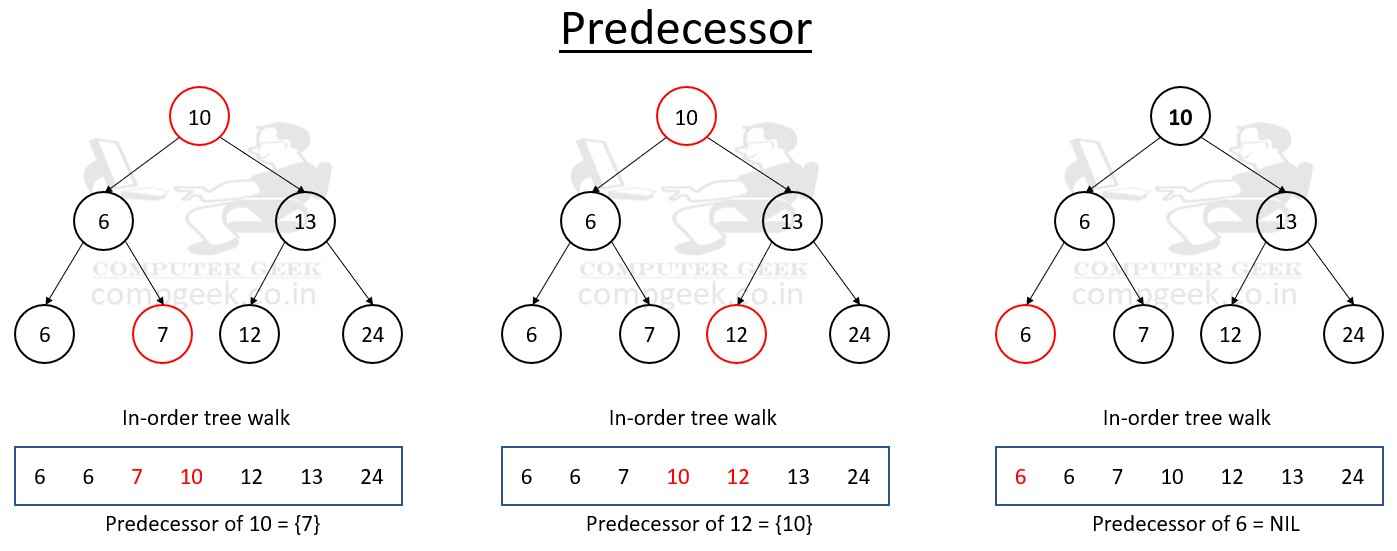
(vi) Predecessor

When traversing a binary search tree in sorted order, the predecessor of a node is the previous node (immediate left adjacent) to it.

Alternately, we may state that, assuming all of the keys are unique, the predecessor of key n is the node with the highest key smaller than key n.

Algorithm

Predecessor(n)

1. Pick the left subtree of n.
2. Predcessor <- Maximum of left subtree
3. If left child is not present
4. then look for the parent of n.
5. if n is right child of parent
6. then Predecessor <- parent.
7. Else, Predecessor = NIL.

Time complexity of finding the predecessor in binary search tree is O(h).

.

(vii) Insert

As the basic rule of binary search tree, insertion simply adds a node to the tree into its correct place. If root has an equal or greater value in comparison to the new node, then new node goes to the left subtree. Also, if root has the lesser value in comparison to the new node, then new node goes to the right subtree.

Algorithm

Insertion(node n)

1. If tree has no node
2. n <- root of the tree
3. Else if, if tree has a node m, and (n ≤ m)
4. left child(m) <- Insertion(node n)
5. Else, right child <- Insertion(node n)

Time complexity of inserting a node in binary search tree is O(h).

If there is a left-skewed tree or right-skewed tree, the time complexity will be O(n).

.

(viii) Delete

The deletion in binary search tree has three types.

The deleted node has

(i) no children.

(ii) One child either left or right.

(iii) Two children.

Trick – The best way to remember the tree deletion is to see in-order tree walk. Before deletion, the in-order tree walk will print the keys in sorted order, and after the deletion, the in-order tree walk will also print the keys in the sorted order. So, we can imagine the tree after the deletion happens.

Example –

(i) The deleted node has no children

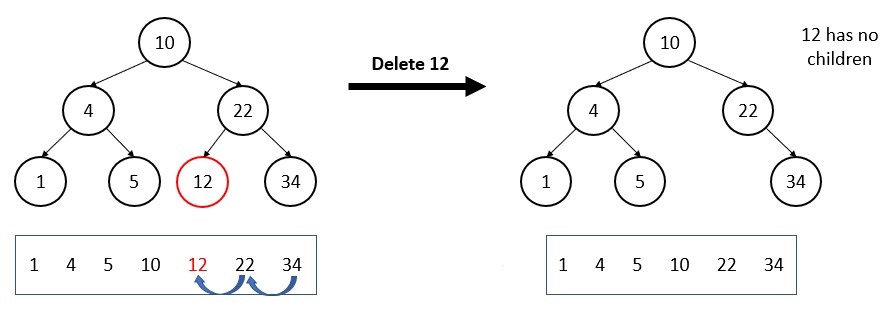
Simply delete the node and do nothing inside the tree.

Let’s see the in-order tree walk. 12 is deleted and the next node or successor of 12 will shift left to take the place of 12. Also, all the other nodes which are right to the 12 will shift left to fill the place.

The in-order tree walk is sorted before and after the deletion happens.

(ii) The deleted node has one child. Either left child or right child.

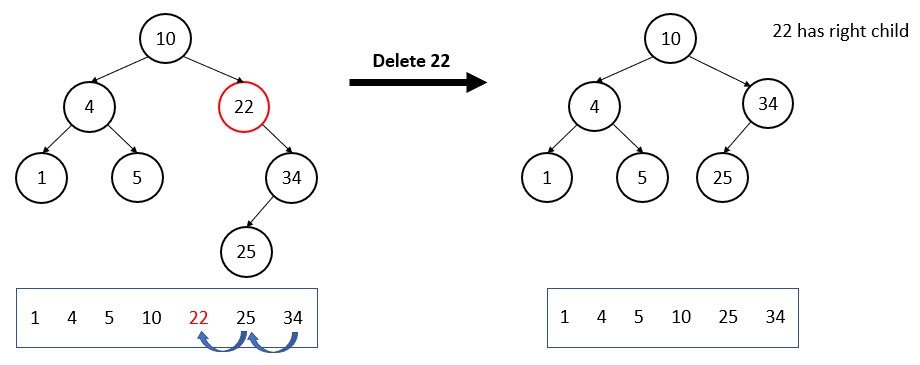
22 is deleted and the next node or successor of 22 will shift left to take the place. Also, all the other nodes which are right to the 22 will shift left to fill the place.

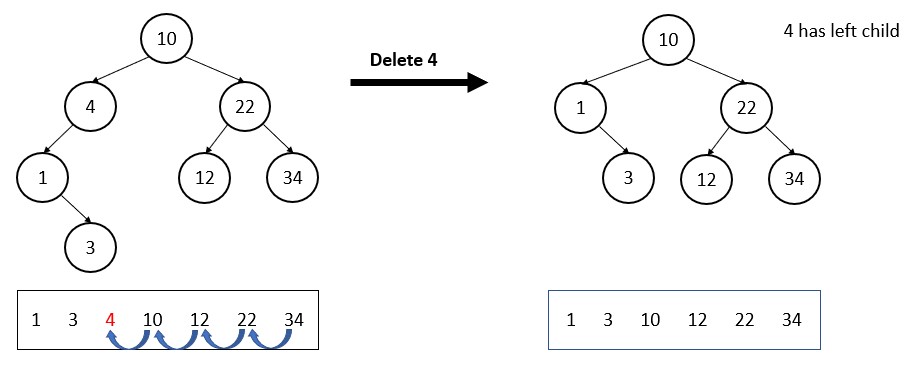
4 is deleted and has only a left child. It means 10 will become the 1’s parent and 3 will be associated to 1 asities.

(iii) The deleted node has both children.

The trick comes into play.

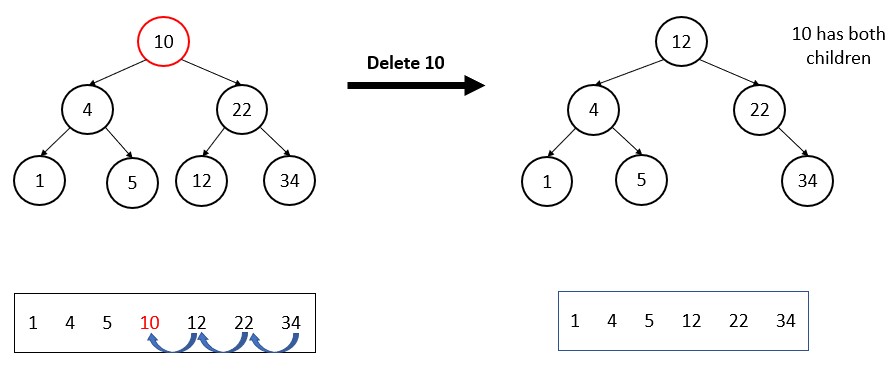
10 has both children. The successor of 10 is 12.

So, 12 will left its place and occupy the 10’s place because in the array 12 will come to 10’s place after deletion. The in-order tree walk print the nodes in sorted array so the right nodes of the deleted node shift left to fill up the space.

Algorithm

DeletionBST(n)

1. If key(n) = NIL
2. delete n
3. Else if, key(n) = only left subtree
4. Delete n and left subtree will take the place of n.
5. Else if, key(n) = only right subtree
6. Delete n and right subtree will take the place of n.
7. else, key(n) = both children are there
8. Find successor of n.
9. Delete n and store its successor into the place of n.

The time complexity of deletion is O(h).