Binary Search Algorithm Simplified
.
Definition
Binary search is a computer algorithm used to efficiently locate a specific element within a sorted list, array, or sequence of data. It follows a divide-and-conquer strategy, repeatedly dividing the search range in half, eliminating half of the remaining elements with each comparison. This process is repeated until the target element is found or the search interval becomes empty.
Binary search is known for its logarithmic time complexity, making it highly effective for searching large datasets.
Binary search was originally mentioned in 1946 by John Mauchly as part of the Moore School Lectures.
.
Working
- Binary Search works by repeatedly dividing the search interval in half.
- It compares the middle element of the interval with the target element and narrows down the search range accordingly.
- If the middle element matches the target, the search is successful.
- If not, the algorithm determines whether the target should be in the left or right half of the interval and continues the search in that portion.
- This process is repeated until the target element is found or the interval becomes empty.
.
Algorithm of Binary Search
- Start with the entire sorted list.
- Calculate the middle index of the current interval: `mid = (low + high) / 2`.
- Compare the middle element with the target element.
- If the middle element is equal to the target, the search is successful.
- If the middle element is less than the target, update `low = mid + 1` and repeat step 2.
- If the middle element is greater than the target, update `high = mid – 1` and repeat step 2.
- Repeat steps 2-6 until `low` is greater than `high`.
.
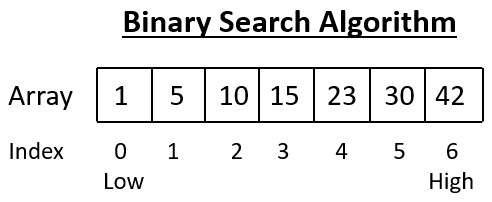
Let’s find the index of the number 23 in the sorted array [1, 5, 10, 15, 23, 30, 42].
1. Initial interval – `low = 0`, `high = 6`.
.
2. Calculate `mid = (0 + 6) / 2 = 3`.

.
3. Compare `arr[3]` (15) with the target (23).
15 < 23
.
4. Since 23 is greater, update `low = mid + 1 = 4`.

.
5. New interval: `low = 4`, `high = 6`.

.
6. Calculate `mid = (4 + 6) / 2 = 5`.

.
7. Compare `arr[5]` (30) with the target (23).
30 > 23
.
8. Since 23 is less, update `high = mid – 1 = 4`.

.
9. New interval: `low = 4`, `high = 4`.

.
10. Calculate `mid = (4 + 4) / 2 = 4`.

.
11. Compare `arr[4]` (23) with the target (23).
23 = 23
Target found at index 4.
// COMPUTER GEEK – compgeek.co.in
// Write a program for Binary Search Algorithm
#include <stdio.h>
// Function to perform binary search
int binarySearch(int arr[], int size, int target)
{
int left = 0;
int right = size – 1;
while (left <= right)
{
int mid = left + (right – left) / 2; // Calculate mid index
if (arr[mid] == target)
{
return mid; // Target found at mid index
}
if (arr[mid] < target)
{
left = mid + 1; // Adjust left pointer if target is on the right side
}
else
{
right = mid – 1; // Adjust right pointer if target is on the left side
}
}
return -1; // Target not found
}
int main()
{
int size, target;
printf(“Enter the size of the array: “);
scanf(“%d”, &size);
int arr[size];
printf(“Enter %d sorted elements:\n”, size);
for (int i = 0; i < size; i++)
{
scanf(“%d”, &arr[i]);
}
printf(“Enter the number to search for: “);
scanf(“%d”, &target);
// Call the binarySearch function
int result = binarySearch(arr, size, target);
if (result != -1)
{
printf(“Element found at index: %d\n”, result);
}
else
{
printf(“Element not found in the array.\n”);
}
return 0;
}
// COMPUTER GEEK – compgeek.co.in
// Write a program for Binary Search Algorithm
#include <iostream>
// Function to perform binary search
int binarySearch(int arr[], int size, int target) {
int left = 0;
int right = size – 1;
while (left <= right) {
int mid = left + (right – left) / 2; // Calculate mid index
if (arr[mid] == target) {
return mid; // Target found at mid index
}
if (arr[mid] < target) {
left = mid + 1; // Adjust left pointer if target is on the right side
} else {
right = mid – 1; // Adjust right pointer if target is on the left side
}
}
return -1; // Target not found
}
int main() {
int size, target;
std::cout << “Enter the size of the array: “;
std::cin >> size;
int arr[size];
std::cout << “Enter ” << size << ” sorted elements:\n”;
for (int i = 0; i < size; i++) {
std::cin >> arr[i];
}
std::cout << “Enter the number to search for: “;
std::cin >> target;
// Call the binarySearch function
int result = binarySearch(arr, size, target);
if (result != -1) {
std::cout << “Element found at index: ” << result << std::endl;
} else {
std::cout << “Element not found in the array.” << std::endl;
}
return 0;
}
// COMPUTER GEEK – compgeek.co.in
// Write a program for Binary Search Algorithm
import java.util.Scanner;
public class BinarySearch {
// Function to perform binary search
public static int binarySearch(int[] arr, int target) {
int left = 0;
int right = arr.length – 1;
while (left <= right) {
int mid = left + (right – left) / 2; // Calculate mid index
if (arr[mid] == target) {
return mid; // Target found at mid index
}
if (arr[mid] < target) {
left = mid + 1; // Adjust left pointer if target is on the right side
} else {
right = mid – 1; // Adjust right pointer if target is on the left side
}
}
return -1; // Target not found
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.print(“Enter the size of the array: “);
int size = scanner.nextInt();
int[] arr = new int[size];
System.out.println(“Enter ” + size + ” sorted elements:”);
for (int i = 0; i < size; i++) {
arr[i] = scanner.nextInt();
}
System.out.print(“Enter the number to search for: “);
int target = scanner.nextInt();
// Call the binarySearch function
int result = binarySearch(arr, target);
if (result != -1) {
System.out.println(“Element found at index: ” + result);
} else {
System.out.println(“Element not found in the array.”);
}
scanner.close();
}
}
# COMPUTER GEEK – compgeek.co.in
# Write a program for Binary Search Algorithm
# Function to perform binary search
def binary_search(arr, target):
left = 0
right = len(arr) – 1
while left <= right:
mid = left + (right – left) // 2 # Calculate mid index
if arr[mid] == target:
return mid # Target found at mid index
if arr[mid] < target:
left = mid + 1 # Adjust left pointer if target is on the right side
else:
right = mid – 1 # Adjust right pointer if target is on the left side
return -1 # Target not found
def main():
size = int(input(“Enter the size of the array: “))
arr = []
print(“Enter”, size, “sorted elements:”)
for _ in range(size):
arr.append(int(input()))
target = int(input(“Enter the number to search for: “))
# Call the binary_search function
result = binary_search(arr, target)
if result != -1:
print(“Element found at index:”, result)
else:
print(“Element not found in the array.”)
if __name__ == “__main__”:
main()
Time Complexity
Best Case Time Complexity – The best case time complexity of binary search is O(1). This happens when the element you’re looking for is exactly in the middle of the sorted list you’re searching through. You find it right away without needing to check any other elements.
.
Average Case Time Complexity – The average case time complexity of binary search is O(log n). Here, ‘n‘ represents the number of elements in the sorted list.
.
Worst Case Time Complexity – The worst case time complexity of binary search is O(log n) as well. Even in the worst case scenario, where the element you’re looking for is the last one checked, binary search efficiently narrows down the search range by half at every step, resulting in a logarithmic time complexity.
.
Space Complexity
Binary Search has a space complexity of O(1), meaning it uses a constant amount of memory regardless of the size of the dataset.
.
Advantages of Binary Search
- Efficient for large datasets.
- Minimizes the number of comparisons required.
- Works well with sorted data.
- Simple and easy to implement.
Disadvantages of Binary Search
- Requires sorted input.
- Doesn’t work well with unsorted or dynamically changing data.
- Might be less efficient compared to other search algorithms for small datasets.
Applications of Binary Search
- Searching in databases and libraries.
- Implementing autocomplete and spell-check features.
- Finding elements in ordered lists or arrays.
- Network routing and IP address lookup.
Binary Search is a powerful algorithm that simplifies the process of searching for specific elements in large datasets. Its efficiency and simplicity make it a valuable tool for various real-world applications in computer science and beyond.
Test Yourself
Q1- How does binary search handle the search process step by step?
Binary search continually divides the search interval in half, compares the middle element with the target, and narrows down the range based on the comparison result.
Q2- If there is an unsorted array of elements and you have to search an element with in the array, then which one will you choose Linear Search or Binary Search.
If you have an unsorted array of elements and you need to search for a specific element within the array, the most appropriate choice would be Linear Search.
Here’s why:
Linear Search: Linear search is a straightforward search algorithm that goes through each element in the array one by one until it finds the target element or exhausts the entire array. It doesn’t require the data to be sorted and can work efficiently for small to moderate-sized datasets.
Binary Search: Binary search, on the other hand, is designed for sorted arrays. It repeatedly divides the search interval in half, which requires the data to be ordered. Using binary search on an unsorted array could lead to incorrect results because the algorithm relies on the order of elements to work effectively.
So, if the array is unsorted, it’s best to use Linear Search to find the desired element within the array.
Q3- What is the primary advantage of binary search over linear search?
Binary search is much faster for large datasets because it reduces the number of comparisons needed to find the target element.
Q4- Explain the worst-case time complexity of binary search and when it occurs.
The worst-case time complexity of binary search is O(log n), which happens when the target element is at the extreme end of the sorted list.
Q5- In a sorted list from 1 to 100, using binary search to find a specific element requires a maximum of __________ comparisons.
In a sorted list from 1 to 100, using binary search to find a specific element requires a maximum of 7 comparisons.
Binary search works by repeatedly dividing the search interval in half. Since you start with a range of 1 to 100, each comparison reduces the range to approximately half of its previous size.
Initial range: 1 – 100 (1 comparison)
After 1st comparison: 1 – 50 (2nd comparison)
After 2nd comparison: 1 – 25 (3rd comparison)
After 3rd comparison: 13 – 25 (4th comparison)
After 4th comparison: 19 – 25 (5th comparison)
After 5th comparison: 22 – 25 (6th comparison)
After 6th comparison: 24 – 25 (7th comparison)
At this point, the search interval is very small (only one or two elements), and you would find the element with one or two more comparisons.
So, the maximum number of comparisons needed to search for an element in a sorted list from 1 to 100 using binary search is 7.
Q6- Discuss a real-life scenario where binary search could be applied effectively.
Imagine you have a physical dictionary, like the ones we used before digital dictionaries became common. You want to find the definition of a specific word in the dictionary. Instead of starting from the beginning and flipping through each page (which would be like linear search), you can use a strategy similar to binary search.
Q7- Can binary search be used to search for duplicate elements in a list? Why or why not?
Binary search is not suitable for finding duplicate elements because it’s designed to locate a single target element.
Q8- What is the main idea behind binary search?
Sorting a list of elements
Dividing the search interval in half
Comparing elements randomly
Combining two lists
Ans – (2)
Explanation – Binary search repeatedly divides the search interval in half to narrow down the search range.
Q9- What is the worst case time complexity of binary search?
O(1)
O(n)
O(log n)
O(n^2)
Ans – (3)
Explanation – Binary search has a worst case time complexity of O(log n), making it efficient for large datasets.
Q10- Binary search is most efficient for
Small datasets
Unsorted datasets
Large datasets
Dynamic datasets
Ans – (3)
Q11- What does the term “divide and conquer” refer to in binary search?
Splitting the data into multiple parts
Repeating the same operation multiple times
Dividing the search interval in half
Combining two sorted lists
Ans – (3)
Explanation – Binary search follows a divide-and-conquer strategy by repeatedly dividing the search interval.
Q12- In binary search, the process continues until:
The target element is found.
The search interval becomes empty.
The list is reversed.
The target element is in the first position.
Ans – (2)
Explanation –
Binary search keeps narrowing down the search interval until there are no more elements left to check.






