Introduction to Bellman-Ford Algorithm
.
The Bellman-Ford algorithm is a fundamental method used in the design and analysis of algorithms.
“It is particularly useful for finding the shortest paths from a single source vertex to all other vertices in a weighted graph, even in the presence of negative weight edges, making it a versatile tool in various applications.”
Bellman-Ford is more versatile as it can handle graphs with negative weight edges and detect negative weight cycles.
.
Bellman-Ford Algorithm Vs. Dijkstra’s Algorithm
Criteria | Bellman-Ford Algorithm | Dijkstra’s Algorithm |
Single Source Shortest Paths | Finds shortest paths from a single source to all other vertices, even with negative weight edges. | Finds shortest paths from a single source to all other vertices, but assumes non-negative weights. |
Time Complexity | O(V * E) | O((V + E) * log(V)) |
Space Complexity | O(V) | O(V + E) |
Negative Weight Edges | Handles graphs with negative weight edges. | Assumes non-negative weights; may produce incorrect results in the presence of negative weights. |
Performance | Slower in general, especially for dense graphs or graphs with negative weight edges. | Faster, particularly in graphs with non-negative weights. |
Optimizations | Can be optimized for certain cases, such as early stopping if no relaxation occurs in an iteration. | Efficient with data structures like priority queues, allowing for quicker updates of distances. |
Use Cases | Suitable for graphs with negative weight edges, where Dijkstra’s algorithm may fail. | Preferred for graphs with non-negative weights due to its efficiency. |
Negative Weight Cycles | Can detect negative weight cycles in the graph. | Does not detect negative weight cycles. |
.
History
The Bellman-Ford algorithm, named after its inventors Richard Bellman and Lester Ford, both were American mathematician and computer scientist, has its roots in the field of operations research and computer science.


The algorithm builds upon foundational concepts in graph theory, which dates back to the 18th century with the work of mathematicians like Leonhard Euler. Euler’s solution to the Seven Bridges of Königsberg problem laid the groundwork for graph theory, which became a fundamental area of study in mathematics and computer science.
Richard Bellman, introduced the concept of dynamic programming in the 1950s. In collaboration with Lester Ford, Bellman extended these ideas to develop an algorithm for solving the single-source shortest path problem in a graph with both positive and negative edge weights.
.
Negative – weight Edges
Negative weight edges in a graph are edges that have weights assigned to them, and these weights are less than zero.
In simpler terms, when you’re looking at a graph where the edges represent connections between points, a negative weight edge means that it gained by you something to traverse that edge.
For example, in a map where cities are represented by points and roads between them by edges, a negative weight edge might signify a road where you gain money or save time by traveling along it. This is contrary to a regular edge where you typically spend time or money to travel along it.
.
Negative Cycles
Negative weight edges can complicate finding the shortest path in a graph. If there are no negative weight cycles reachable from the starting point, the shortest path remains clear even if it has negative values.
However, if such cycles exist, defining the shortest path becomes unclear. If a negative weight is encountered along the path, it’s labelled as negative infinity, indicating ambiguity in defining the shortest path.
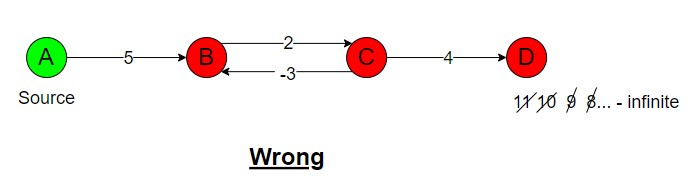
Note – Both Dijkstra’s algorithm and the Bellman-Ford algorithm are versatile and can be used effectively in both directed and undirected graphs to find shortest paths.
.
Algorithm of Bellman-Ford
G – Weighted graph represented as an adjacency list or matrix.
Source – The source vertex from which shortest paths are calculated.
Initialization
- Create an array dist[] of size V (number of vertices in G) to store the shortest distance from the source vertex to each vertex.
- Initialize dist[source] = 0 and dist[v] = Infinity for all other vertices v.
Main Algorithm
- Repeat the following step V – 1 times (where V is the number of vertices in the graph).
- For each edge (u, v) in the graph, relax the edge.
- If dist[u] + weight(u, v) < dist[v], update dist[v] = dist[u] + weight(u, v) and set prev[v] = u.
- After V – 1 iterations, all shortest paths from the source vertex are found unless there are negative weight cycles.
Check for Negative Cycles
- Iterate over all edges (u, v) in the graph and check if there is any improvement in dist[v] by relaxing the edge (u, v).
- If dist[u] + weight(u, v) < dist[v], then there exists a negative weight cycle reachable from the source vertex.
Optionally, you can perform an additional step to trace back and identify the vertices in the negative weight cycle.
.
Example

.
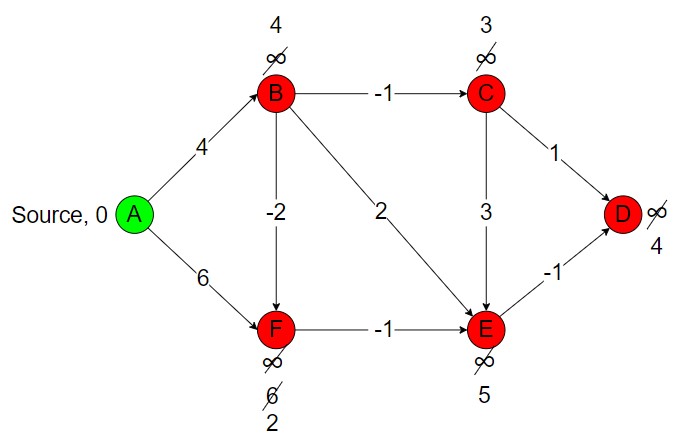
Now, let’s apply the Bellman-Ford algorithm with source vertex A.
Initialization
Initialize dist[] array
dist[] = {0, ∞, ∞, ∞, ∞, ∞}

.
Perform relaxation
V = {A, B, C, D, E, F} in this graph. So, to get the shortest distance in vertex, the edges need to relax V – 1 times (5 times).
Relaxation refers to the process of updating the shortest distance estimate to a vertex if a shorter path to that vertex is discovered.
The edges are (A, B), (A, F), (F, E), (B, F), (B, C), (B, E), (C, E), (C, D), (E, D).
Step by step check all the edges and write the shortest weight in vertices by applying a formula
Formula is, dist[v] = min(dist[v], dist[u] + weight(u, v))
.
Iteration 1
.
For (A, B), dist[B] = min(∞, 0 + 4) = 4
For (A, F), dist[F] = min(∞, 0 + 6) = 6
For (F, E), dist[E] = min(∞, 6 – 1) = 5
For (B, F), dist[F] = min(6, 4 – 2) = 2
For (B, C), dist[C] = min(∞, 4 – 1) = 3
For (B, E), dist[E] = min(5, 4 + 2) = 5
For (C, E), dist[E] = min(5, 3 + 3) = 5
For (C, D), dist[D] = min(∞, 3 + 1) = 4
For (E, D), dist[D] = min(∞, 5 – 1) = 4
.
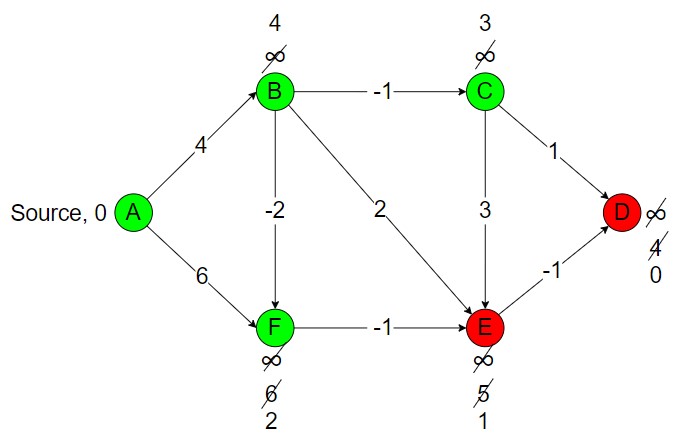
Iteration 2
.
For (A, B), dist[B] = min(4, 0 + 4) = 4
For (A, F), dist[F] = min(2, 0 + 6) = 2
For (F, E), dist[E] = min(5, 2 – 1) = 1
For (B, F), dist[F] = min(2, 4 – 2) = 2
For (B, C), dist[C] = min(3, 4 – 1) = 3
For (B, E), dist[E] = min(1, 4 + 2) = 1
For (C, E), dist[E] = min(1, 3 + 3) = 1
For (C, D), dist[D] = min(4, 3 + 1) = 4
For (E, D), dist[D] = min(4, 1 – 1) = 0
Check for negative weight cycles
Relax all edges one more time.
Iteration 3

.
For (A, B), dist[B] = min(4, 0 + 4) = 4
For (A, F), dist[F] = min(2, 0 + 6) = 2
For (F, E), dist[E] = min(5, 2 – 1) = 1
For (B, F), dist[F] = min(2, 4 – 2) = 2
For (B, C), dist[C] = min(3, 4 – 1) = 3
For (B, E), dist[E] = min(1, 4 + 2) = 1
For (C, E), dist[E] = min(1, 3 + 3) = 1
For (C, D), dist[D] = min(4, 3 + 1) = 4
For (E, D), dist[D] = min(4, 1 – 1) = 0
In iteration 3, No changes in dist[], so no negative weight cycles detected.
After the Bellman-Ford algorithm completes, the shortest distances from vertex A to all other vertices are
A = 0
B = 4,
C = 3,
D = 0,
E = 1,
F = 2.
Source Code of Bellman Ford Algorithm
// COMPUTER GEEK – compgeek.co.in
// Write a program for Bellman Ford Method
#include <stdio.h>
#include <stdlib.h>
#include <limits.h>
#define MAX_VERTICES 100
struct Edge {
int source, destination, weight;
};
struct Graph {
int V, E;
struct Edge* edges;
};
struct Graph* initializeGraph(int V, int E) {
struct Graph* graph = (struct Graph*)malloc(sizeof(struct Graph));
graph->V = V;
graph->E = E;
graph->edges = (struct Edge*)malloc(E * sizeof(struct Edge));
return graph;
}
void bellmanFord(struct Graph* graph, int source) {
int V = graph->V;
int E = graph->E;
int dist[MAX_VERTICES];
for (int i = 0; i < V; i++)
dist[i] = INT_MAX;
dist[source] = 0;
for (int i = 1; i <= V – 1; i++) {
for (int j = 0; j < E; j++) {
int u = graph->edges[j].source;
int v = graph->edges[j].destination;
int weight = graph->edges[j].weight;
if (dist[u] != INT_MAX && dist[u] + weight < dist[v])
dist[v] = dist[u] + weight;
}
}
for (int i = 0; i < E; i++) {
int u = graph->edges[i].source;
int v = graph->edges[i].destination;
int weight = graph->edges[i].weight;
if (dist[u] != INT_MAX && dist[u] + weight < dist[v]) {
printf(“Graph contains negative weight cycle. Cannot find shortest paths.\n”);
return;
}
}
printf(“Shortest distances from source vertex %d:\n”, source);
for (int i = 0; i < V; i++)
printf(“Vertex %d: %d\n”, i, dist[i]);
}
int main() {
int V, E;
printf(“Enter the number of vertices and edges: “);
scanf(“%d %d”, &V, &E);
struct Graph* graph = initializeGraph(V, E);
printf(“Enter edges in format [source destination weight]:\n”);
for (int i = 0; i < E; i++) {
int source, destination, weight;
scanf(“%d %d %d”, &source, &destination, &weight);
graph->edges[i] = (struct Edge){source, destination, weight};
}
int sourceVertex;
printf(“Enter the source vertex: “);
scanf(“%d”, &sourceVertex);
bellmanFord(graph, sourceVertex);
free(graph->edges);
free(graph);
return 0;
}
/*
Output
Enter the number of vertices and edges: 6 9
Enter edges in format [source destination weight]:
0 1 4
0 5 6
1 2 -1
1 4 2
1 5 -2
5 4 -1
2 3 1
2 4 3
4 3 -1
Enter the source vertex: 0
Shortest distances from source vertex 0:
Vertex 0: 0
Vertex 1: 4
Vertex 2: 3
Vertex 3: 0
Vertex 4: 1
Vertex 5: 2
*/
// COMPUTER GEEK – compgeek.co.in
// Write a program for Bellman Ford Method
#include <iostream>
#include <vector>
#include <climits>
using namespace std;
// Define a structure to represent an edge in the graph
struct Edge {
int source, destination, weight;
};
// Define a structure to represent the graph
struct Graph {
int V, E; // V is the number of vertices, E is the number of edges
vector<Edge> edges; // Vector to store edges
};
// Bellman-Ford algorithm function
void bellmanFord(Graph& graph, int source) {
int V = graph.V;
int E = graph.E;
// Initialize distance array
vector<int> dist(V, INT_MAX);
dist[source] = 0;
// Relax all edges V-1 times
for (int i = 1; i <= V – 1; i++) {
for (int j = 0; j < E; j++) {
int u = graph.edges[j].source;
int v = graph.edges[j].destination;
int weight = graph.edges[j].weight;
// Relaxation step
if (dist[u] != INT_MAX && dist[u] + weight < dist[v])
dist[v] = dist[u] + weight;
}
}
// Check for negative weight cycles
for (int i = 0; i < E; i++) {
int u = graph.edges[i].source;
int v = graph.edges[i].destination;
int weight = graph.edges[i].weight;
if (dist[u] != INT_MAX && dist[u] + weight < dist[v]) {
cout << “Graph contains negative weight cycle. Cannot find shortest paths.” << endl;
return;
}
}
// Print the shortest distances
cout << “Shortest distances from source vertex ” << source << “:” << endl;
for (int i = 0; i < V; i++)
cout << “Vertex ” << i << “: ” << dist[i] << endl;
}
int main() {
int V, E;
cout << “Enter the number of vertices and edges: “;
cin >> V >> E;
// Create a graph object
Graph graph;
graph.V = V;
graph.E = E;
cout << “Enter edges in format [source destination weight]:” << endl;
for (int i = 0; i < E; i++) {
int source, destination, weight;
cin >> source >> destination >> weight;
graph.edges.push_back({source, destination, weight});
}
int sourceVertex;
cout << “Enter the source vertex: “;
cin >> sourceVertex;
// Call Bellman-Ford algorithm
bellmanFord(graph, sourceVertex);
return 0;
}
// COMPUTER GEEK – compgeek.co.in
// Write a program for Bellman Ford Method
import java.util.*;
// Define a class to represent an edge in the graph
class Edge {
int source, destination, weight;
public Edge(int source, int destination, int weight) {
this.source = source;
this.destination = destination;
this.weight = weight;
}
}
// Define a class to represent the graph
class Graph {
int V, E; // V is the number of vertices, E is the number of edges
List<Edge> edges; // List to store edges
public Graph(int V, int E) {
this.V = V;
this.E = E;
edges = new ArrayList<>();
}
}
// Bellman-Ford algorithm function
class BellmanFord {
void bellmanFord(Graph graph, int source) {
int V = graph.V;
int E = graph.E;
// Initialize distance array
int[] dist = new int[V];
Arrays.fill(dist, Integer.MAX_VALUE);
dist[source] = 0;
// Relax all edges V-1 times
for (int i = 1; i <= V – 1; i++) {
for (int j = 0; j < E; j++) {
int u = graph.edges.get(j).source;
int v = graph.edges.get(j).destination;
int weight = graph.edges.get(j).weight;
// Relaxation step
if (dist[u] != Integer.MAX_VALUE && dist[u] + weight < dist[v])
dist[v] = dist[u] + weight;
}
}
// Check for negative weight cycles
for (int i = 0; i < E; i++) {
int u = graph.edges.get(i).source;
int v = graph.edges.get(i).destination;
int weight = graph.edges.get(i).weight;
if (dist[u] != Integer.MAX_VALUE && dist[u] + weight < dist[v]) {
System.out.println(“Graph contains negative weight cycle. Cannot find shortest paths.”);
return;
}
}
// Print the shortest distances
System.out.println(“Shortest distances from source vertex ” + source + “:”);
for (int i = 0; i < V; i++)
System.out.println(“Vertex ” + i + “: ” + dist[i]);
}
}
class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.print(“Enter the number of vertices and edges: “);
int V = scanner.nextInt();
int E = scanner.nextInt();
// Create a graph object
Graph graph = new Graph(V, E);
System.out.println(“Enter edges in format [source destination weight]:”);
for (int i = 0; i < E; i++) {
int source = scanner.nextInt();
int destination = scanner.nextInt();
int weight = scanner.nextInt();
graph.edges.add(new Edge(source, destination, weight));
}
System.out.print(“Enter the source vertex: “);
int sourceVertex = scanner.nextInt();
// Call Bellman-Ford algorithm
BellmanFord bellmanFord = new BellmanFord();
bellmanFord.bellmanFord(graph, sourceVertex);
scanner.close();
}
}
# COMPUTER GEEK – compgeek.co.in
# Write a program for Bellman Ford Method
class Edge:
def __init__(self, source, destination, weight):
self.source = source
self.destination = destination
self.weight = weight
class Graph:
def __init__(self, V, E):
self.V = V # Number of vertices
self.E = E # Number of edges
self.edges = [] # List to store edges
class BellmanFord:
def bellman_ford(self, graph, source):
dist = [float(‘inf’)] * graph.V
dist[source] = 0
# Relax all edges V-1 times
for _ in range(graph.V – 1):
for edge in graph.edges:
u, v, weight = edge.source, edge.destination, edge.weight
if dist[u] != float(‘inf’) and dist[u] + weight < dist[v]:
dist[v] = dist[u] + weight
# Check for negative weight cycles
for edge in graph.edges:
u, v, weight = edge.source, edge.destination, edge.weight
if dist[u] != float(‘inf’) and dist[u] + weight < dist[v]:
print(“Graph contains negative weight cycle. Cannot find shortest paths.”)
return
# Print the shortest distances
print(“Shortest distances from source vertex”, source)
for i in range(graph.V):
print(“Vertex”, i, “:”, dist[i])
if __name__ == “__main__”:
V, E = map(int, input(“Enter the number of vertices and edges: “).split())
graph = Graph(V, E)
print(“Enter edges in format [source destination weight]:”)
for _ in range(E):
source, destination, weight = map(int, input().split())
graph.edges.append(Edge(source, destination, weight))
source_vertex = int(input(“Enter the source vertex: “))
bellman_ford = BellmanFord()
bellman_ford.bellman_ford(graph, source_vertex)
Enter the number of vertices and edges: 6 9
Enter edges in format [source destination weight]:
0 1 4
0 5 6
1 2 -1
1 4 2
1 5 -2
5 4 -1
2 3 1
2 4 3
4 3 -1
Enter the source vertex: 0
Shortest distances from source vertex 0:
Vertex 0: 0
Vertex 1: 4
Vertex 2: 3
Vertex 3: 0
Vertex 4: 1
Vertex 5: 2
Time Complexity
Best Case Complexity – In the best case, when the initial guess (distance) is already the shortest path, the algorithm may iterate through all edges once, resulting in a time complexity of O(E).
Average Case Complexity – In the average case, the algorithm may iterate through all edges (E) for each of the vertices (V), resulting in O(VE) time complexity.
Worst Case Complexity – In the worst case, the algorithm may iterate through all edges (E) for each of the vertices (V), resulting in O(VE) time complexity.
If we consider a dense graph where the number of edges E is proportional to V2, such as in a complete graph, the time complexity of the Bellman-Ford algorithm can indeed reach O(V3).
.
Space Complexity
Space complexity is O(V), where V is the number of vertices. This is because we need to maintain a distance array of size V to store the shortest distances from the source vertex to all other vertices.
.
Advantages
Handles Negative Weight Edges – Unlike Dijkstra’s algorithm, which does not work with negative weight edges, Bellman-Ford can handle graphs with negative weight edges. This flexibility allows it to be applied in a wider range of scenarios.
Detects Negative Cycles – Bellman-Ford can detect the presence of negative weight cycles in the graph. This capability is valuable in various applications where identifying cycles with negative weights is necessary, such as in financial modelling or network routing.
Works with Distributed Systems – Bellman-Ford is suitable for distributed systems where each node may only have partial knowledge of the network. It can be implemented in a decentralized manner, making it useful in scenarios where a centralized view of the entire network is not feasible.
Simple Implementation – The algorithm is relatively easy to implement compared to some other shortest path algorithms like Dijkstra’s algorithm with priority queues. Its simplicity makes it accessible and understandable, even for those new to graph algorithms.
No Requirements for Heaps or Priority Queues – Unlike Dijkstra’s algorithm, which typically requires heaps or priority queues for efficient implementation, Bellman-Ford does not have such requirements. This makes it more straightforward to implement and suitable for scenarios where priority queues are not available or practical.
.
Disadvantages
Higher Time Complexity – Bellman-Ford has a time complexity of O(VE) in the worst case, where V is the number of vertices and E is the number of edges. This makes it less efficient compared to other algorithms like Dijkstra’s algorithm, which has a time complexity of O((V+E) logV).
Less Efficient on Dense Graphs – The time complexity reaches to V2 and in complete graph, worst case value is V3.
Inefficient with Non-Negative Graphs – Its performance suffers when applied to graphs without negative weight edges. In such cases, algorithms like Dijkstra’s algorithm are more efficient.
.
Application
Network Routing – Bellman-Ford is used in computer networking protocols, such as the Routing Information Protocol (RIP), to determine the best path for data packets to travel from a source to a destination across a network of routers.
Telecommunications – In telecommunications networks, Bellman-Ford helps optimize the flow of data and signals by finding the shortest paths between network nodes, which can include switches, cell towers, and base stations.
Traffic Management – Bellman-Ford can be employed in transportation and traffic management systems to optimize traffic flow, minimize congestion, and calculate the shortest routes for vehicles traveling between locations.
Flight Navigation – In aviation, Bellman-Ford aids in flight path planning by determining the most efficient routes for aircraft to travel between airports while considering factors such as airspace restrictions and weather conditions.
Resource Allocation – The algorithm is utilized in resource allocation and project management systems to schedule tasks, allocate resources, and optimize workflows by identifying the most efficient paths to complete projects within given constraints.
Test Yourself
Q1- Explain the concept of negative weight edges in a graph and how the Bellman-Ford algorithm handles them.
Negative weight edges are edges in a graph with weights that are less than zero. The Bellman-Ford algorithm can handle graphs with negative weight edges by iteratively relaxing edges to find the shortest paths from a source vertex to all other vertices, even in the presence of negative weights.
Q2- Discuss the significance of detecting negative weight cycles in the context of the Bellman-Ford algorithm.
Detecting negative weight cycles is crucial in the Bellman-Ford algorithm as it helps identify scenarios where the shortest path cannot be determined due to the presence of cycles with negative weights. This capability allows the algorithm to avoid erroneous results and handle complex graph structures effectively.
Q3- Compare and contrast the time complexity of the Bellman-Ford algorithm with other shortest path algorithms like Dijkstra’s algorithm.
The Bellman-Ford algorithm has a time complexity of O(VE), where V is the number of vertices and E is the number of edges. In contrast, Dijkstra’s algorithm has a time complexity of O((V+E) logV).
While Dijkstra’s algorithm is more efficient for graphs with non-negative weights, Bellman-Ford is more versatile and can handle negative weight edges.
Also, Bellman ford is slower than Dijkstra’s algorithm.
Q4- Explain how the Bellman-Ford algorithm can be adapted to detect negative weight cycles in a graph.
To detect negative weight cycles, the Bellman-Ford algorithm performs an additional relaxation step after completing V – 1 iterations. If any distances are updated during this additional step, it indicates the presence of a negative weight cycle reachable from the source vertex.
Q5- Explain the process of relaxation in the Bellman-Ford algorithm and its significance in finding the shortest paths in a graph.
Relaxation in the Bellman-Ford algorithm involves updating the shortest distance estimates to vertices if a shorter path to that vertex is discovered. This process is repeated iteratively until no further improvements can be made, ensuring that the shortest paths from the source vertex to all other vertices are found.
Q6- In what scenarios is the Bellman-Ford algorithm favoured over Dijkstra’s despite being slower?
Bellman-Ford is preferred when dealing with graphs containing negative weight edges or when the presence of negative weight cycles needs to be detected. It is also suitable for distributed systems and scenarios where priority queues are not available.
Q7- Explain how the Bellman-Ford algorithm can be optimized for certain cases to improve its efficiency.
The Bellman-Ford algorithm can be optimized by implementing techniques such as early stopping if no relaxation occurs in an iteration or by using data structures like priority queues to speed up updates of distances. These optimizations can help reduce the overall runtime of the algorithm.
Q8- Discuss real-world applications where the Bellman-Ford algorithm finds significant use and its impact on various domains.
The Bellman-Ford algorithm is widely used in network routing protocols, telecommunications networks, traffic management systems, flight navigation, resource allocation, financial modelling, robotics, autonomous vehicles, and urban planning. Its versatility and ability to handle complex graph structures make it a valuable tool in optimizing various real-world systems and processes.
Q9- What is the purpose of relaxation in the Bellman-Ford algorithm?
To compute the shortest path from one vertex to all other vertices
To detect negative weight cycles in the graph
To update the shortest distance estimates if a shorter path is found
To initialize the distance array with infinite distances
Ans – (3)
Explanation – Relaxation in the Bellman-Ford algorithm involves updating the shortest distance estimates to vertices if a shorter path to that vertex is discovered.
Q10- Which data structure is used to store edges in the Bellman-Ford algorithm?
Array
Linked list
Heap
Queue
Ans – (1)
Explanation – Edges in the Bellman-Ford algorithm is typically stored using an array data structure.
Q11- In which scenario might the Bellman-Ford algorithm be preferred over Dijkstra’s algorithm?
When the graph has non-negative weights
When the graph is dense
When the graph contains negative weight edges
When the graph is undirected
Ans – (3)
Explanation – Bellman-Ford is preferred for graphs with negative weight edges, as it can handle such scenarios effectively.
Q12- What is the time complexity of the Bellman-Ford algorithm in the worst case in a complete graph?
O(V log V)
O(V3)
O(VE)
O(V2)
Ans – (2)
Explanation – The worst-case time complexity of the Bellman-Ford algorithm is O(V3) in a complete graph, where V is the number of vertices and E is the number of edges.






