B-Tree (Multiway Tree)

Multi-Way Tree

A multi-way tree is a tree where each node has more than 1 key and each node has more than two children.

A 4-way tree or order-4 tree has 3 keys in each node and 4 ways, or children.

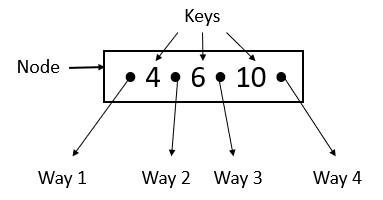
Ques- Why do we use multiway trees?

Suppose you are using an AVL tree or a red-black tree, which are self-balancing binary search trees, and their time complexity of searching, insertion, and deletion is O(h). where h is the height of the tree. If h increases then time complexity will also increase and if h decreases then time complexity also decreases.

Accessing main memory takes about 100 times more time than the time of an arithmetic operation, and accessing disk memory takes about 10000 times more time than the time of an arithmetic operation. This means that we have to reduce the memory access and keep the input numbers in the cache memory, which is the fastest memory. Storage is less in cache memory, so each and every number cannot come in it if we are accessing a very huge random file.

Suppose the height of an AVL tree or a red-black tree is 25, which means there are many numbers in it. Each number is stored in a separate memory block, so if we need to access all 25 memory blocks for data, it will take the longest possible amount of time, or worst-case time.

That’s why Bayer and McCreight designed multi-way tree to reduce the height and time complexity of the tree.

A multi-way tree has two types. The first is a B tree, and the second is a B+ tree.

B Tree

When working at Boeing Research Labs, Rudolf Bayer and Edward M. McCreight developed the B-tree to effectively manage the index pages for huge random-access files.

Neither Bayer nor McCreight clarified what the “B” stands for, Bayer, balanced, or broad. So those who say b is for balanced tree, they say it wrong.

B trees are also called height-balanced m-way trees. It is also called a “broad tree” because it’s a fat tree with a short height. The searching, insertion, and deletion operations have a time complexity of O(h), where h is the height of the tree. So, the b tree has a low height and it is an advantage for us to run the operations in a very less time.

Knuth’s define that a B-tree of order m or known as m-way tree is a tree that matches the following constraints. 

1. Each node n has at most m-1 keys and at most m children. Root node has two or more children.
2. All keys in a node must be in non-decreasing order key₁ ≤ key₂ ≤ key₃ ≤ … ≤ key_n-1 ≤ key_n.
3. Each internal node must have at least ⌈m/2⌉ children.
4. All leaf nodes are at the same level.

We have understood the order of the tree. Now we talk about the degree of a node in the B tree.

The degree of a node is determined by the number of its children. If a node has degree 2, then it has two children.

The maximum and minimum keys that a node can hold are bound. The minimum degree of the B-tree, which is a fixed integer with a value greater than two (t ≥ 2), can be used to represent these bounds:

1. Each node must have t-1 keys, except the root. This means that every internal node except for the root has t or more children. The root of the tree must include at least one key if it is not empty.
2. Each node can hold a maximum of 2t-1 keys. An internal node can therefore have a maximum of 2t children. If a node has exactly 2t-1 keys, we say it is full.

Note – Some students want to insert the keys into the b-tree if they have the order, but if the question has only the minimum degree, they can’t create the tree. I’ll explain the relationship between order and degree in the insertion part.

Insertion into a b-tree

1. Always insert the key into a leaf node.
2. Median key is moved up to its parent’s node during splitting.

Show the result of inserting the following items in an initially empty B-tree of degree t= 2.

Input is –

F, S, Q, K, C, L, H, T, V, W, M, R, N, P, A, B, X, Y, D, Z, E

Ans-

Minimum degree (t) = 2

Maximum degree = 2t -1 = 2(2) – 1 = 3

It means that a node has 3 keys and at most 4 children. So, the order is 4.

Insert F, S, Q

The tree has 3 keys and 4 children.

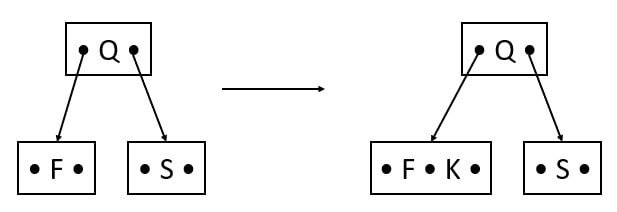
Insert K

The node is completely full, so before inserting K, we have to split the keys. Q is the median will be the root and F and S are its left child and right child.

After splitting, insert K in leaf.

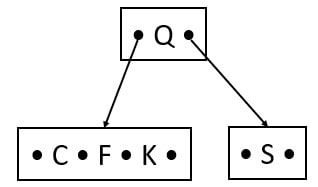
Insert C

C comes before F. So, C is the left key to the F in the leaf.

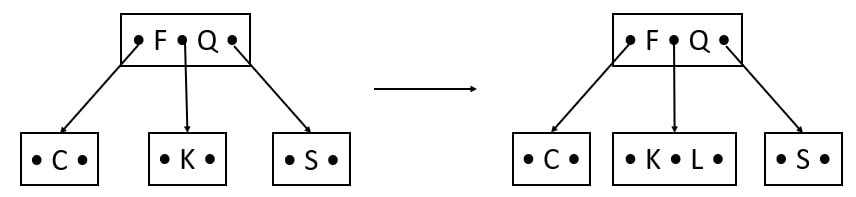
Insert L

L comes after the K key, but the left child, CFK, is full. So, before inserting L, we have to split the keys. F is the median will be the root and C and K are the left and right child of F.

After splitting, insert L in leaf.

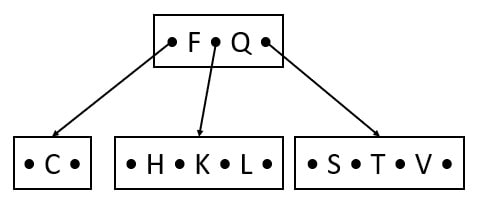
Insert H, T, V

H comes before K. So, H is the left key to the K in the leaf.

T and V comes after S, So T and V are right keys to the S.

Insert W

W comes after V key, but the right child STV is full. So, before inserting W, we have to split the keys. T is the median will be the root. S and V are the left and right child of T.

After splitting, insert W into the leaf.

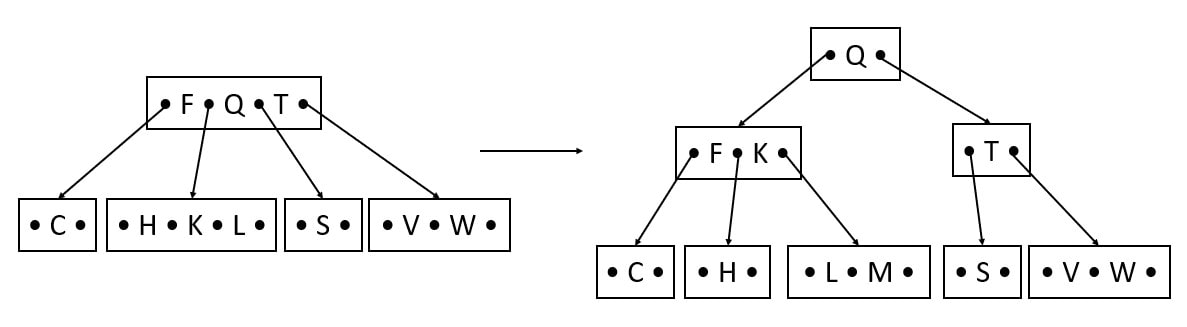
Insert M

M comes after L key, but the child HKL is full. So, before inserting M we have to split the keys. K is the median will be the root but root FQT is also full. So, Q is the median will be the new root and F and T are the left and right child of Q.

After splitting, insert K after F, and H and L are the left and right children of K.

After splitting, insert M in the leaf.

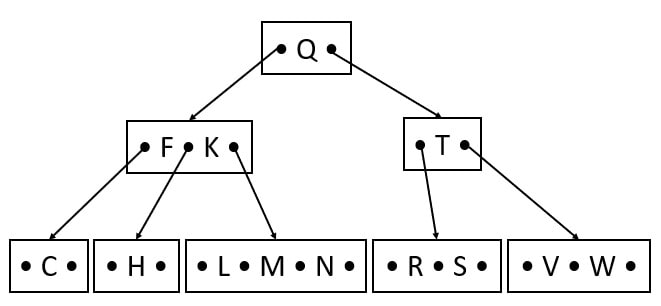
Insert R, N

R comes before S. So, R is the left key to the S in leaf.

N comes after M. So, N is the right key to the M in the leaf.

Insert P

P comes after the N key, but the child LMN is full. So, before inserting P, we have to split the keys. M, the median, will be moved up, and L and N are the left and right children of M, respectively.

After splitting, insert P in the leaf.

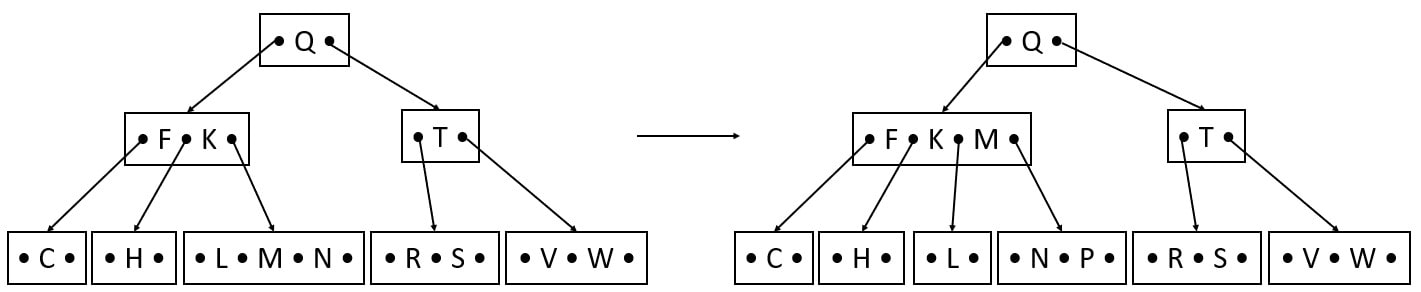
Insert A, B, X

A and B come before C. So, A and B left key to the C in leaf.

X comes after W. So, X is the right key to the W in leaf.

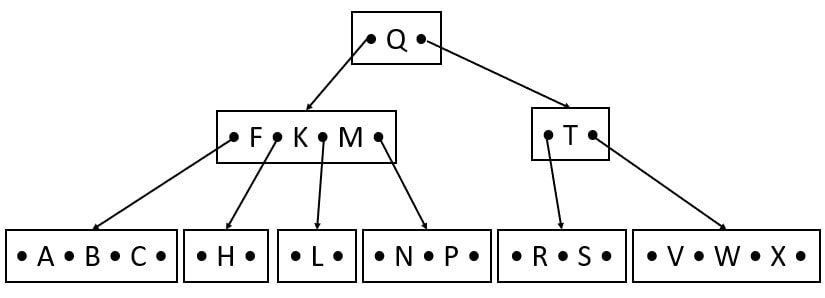
Insert Y

Y comes after X, but the child VWX is full. So, before inserting Y, we have to split the keys. W is the median that will be moved up, and V and X are the left and right children of W.

After splitting, insert Y into the leaf.

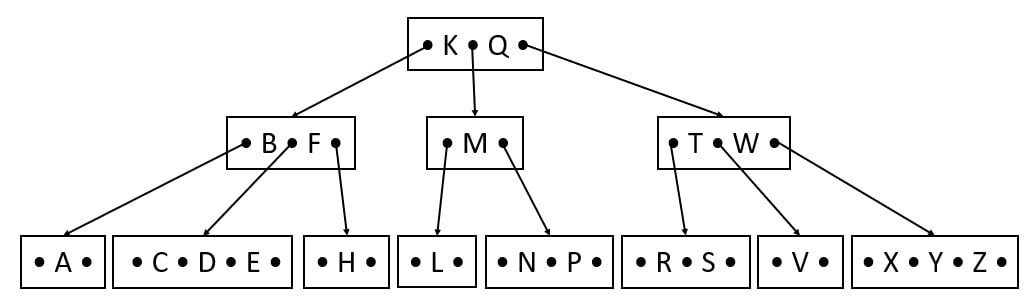
Insert D, Z, E

D comes after C, but the child ABC is full. So, before inserting D, we have to split the keys. B is the median, which will be moved up, but root FKM is also full. So, K is the median and will be the root, and F and M are the left and right children of K.

After splitting, insert B before F, and A and C are the left and right children of B.

After splitting, insert D in the leaf.

Z comes after Y. So, Z is the right key to the Y in leaf.

E comes after D. So, E is right key to the D in leaf.

Algorithm of Insertion in B tree

InsertionBTree(n, k)

1. If tree has no node
2. then insert a key in new node as the root.
3. else search a vacant position in leaf node to add the key in sorted order.
4. If leaf node is completely full
5. Split the node by median key as a parent of left and right keys child.
6. Repeat the splitting until the node is completely full.

Deletion in a B-Tree

Deletion is a very complex operation in b tree. When deleting, two properties must always be considered.

1. A node should have at least minimum degree t.
2. All non-leaf node child pointers must have children.

Input is

There are many scenarios of deletion

CASE 1

• If deleted key is the leaf node,
• Keys in the leaf node > minimum keys require for b tree

Then this is a straightforward deletion. No further operations are required.

Delete D

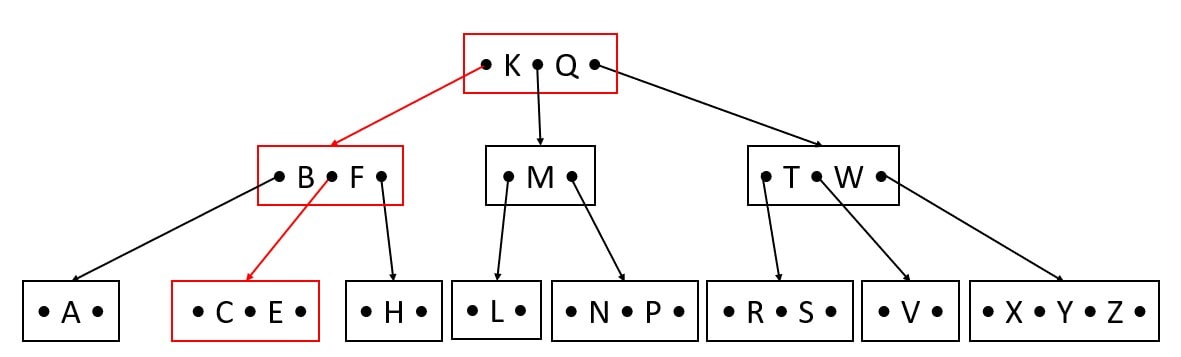
CASE 2

• If deleted key is the leaf node,
• Keys in the leaf node = minimum keys require for b tree

Then after deletion node will violate the property of B tree.

Solution – The deleted node can borrow a key from the left sibling. If left sibling does not have more keys then you can borrow from right sibling.

If H is deleted, the left sibling’s biggest number E will take its parent F place, and F will replace H.

Delete H

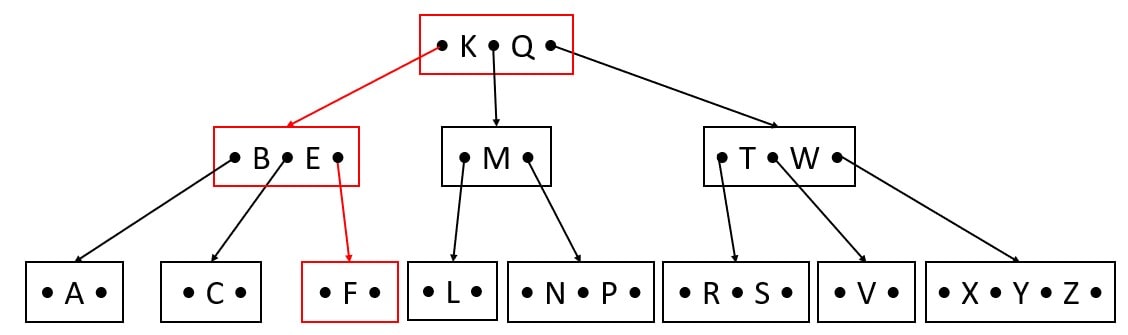
Delete L

If L is deleted, the right sibling’s smallest number N will take its parent M place, and M will replace L.

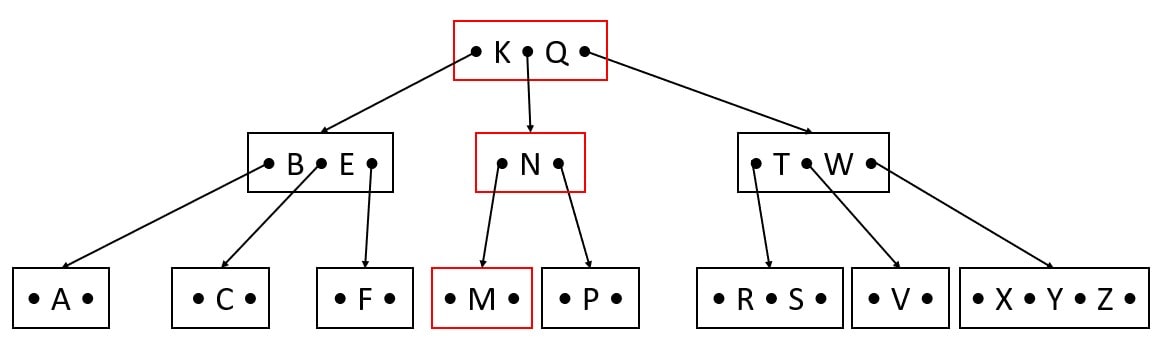
CASE 3

• If deleted key is the leaf node,
• Keys in the leaf node = minimum keys require for b tree
• Can not borrow the key from left and right sibling because they only have minimum number of keys.

Then after deletion node will violate the property of B tree.

Solution – Merge the siblings and the minimum of parent node and replace this with deleted node.

Delete C

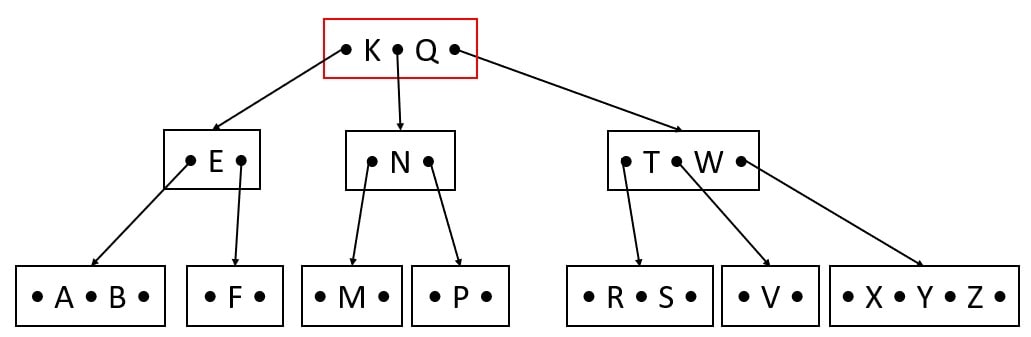
CASE 4

• If deleted key is an internal node.
• Find the immediate predecessor of the deleted key and replace it.

Delete T

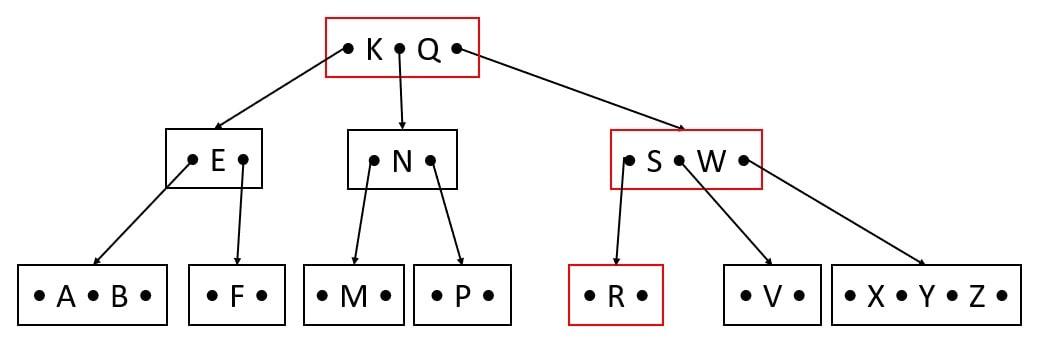
S is the immediate predecessor of T, Hence S replaces T.

• If immediate predecessor has minimum key, then find the immediate successor of deleted key and replace it.

Delete W

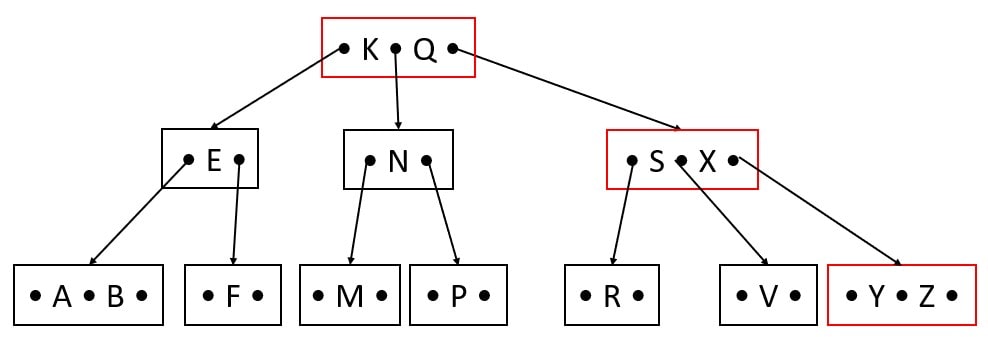
X is the immediate successor of W, Hence X replaces W.

Delete X

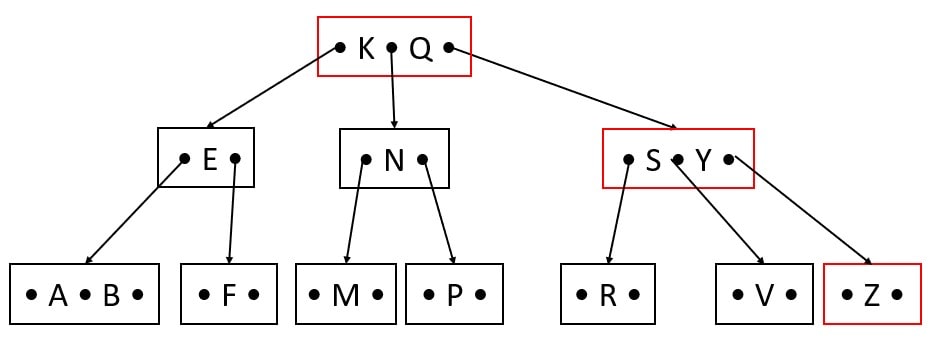
Y is the immediate successor of X, Hence Y replaces X.

• If immediate predecessor and immediate successor have minimum key only, then merge the predecessor and successor.

Delete Y

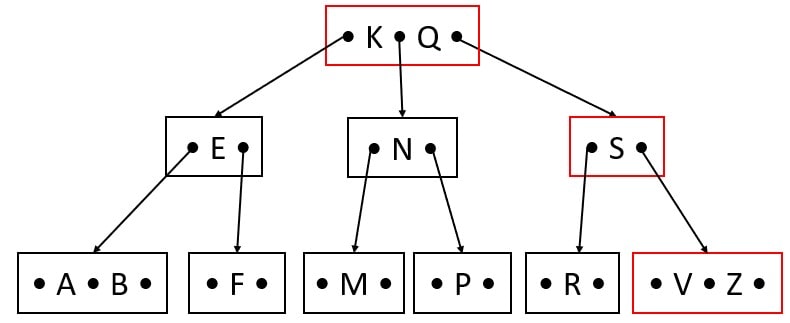
Key Y predecessor V and Successor Z are merged.

CASE 5

• If deleted key is Root node.
• Find the immediate predecessor of deleted key and replace it with the deleted root node.
• Now we have to follow Case 1, Case 2 and Case3, as the immediate predecessor of deleted root node is in the leaf node of the tree.

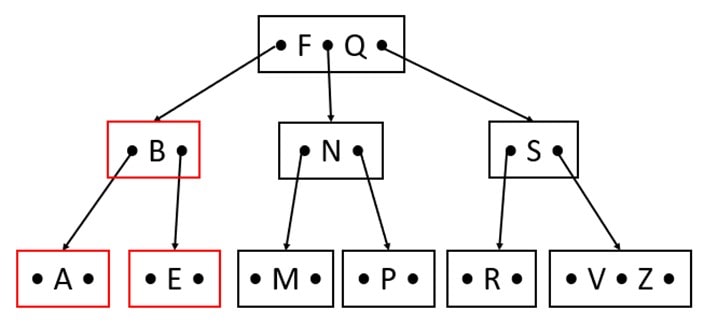
Delete K

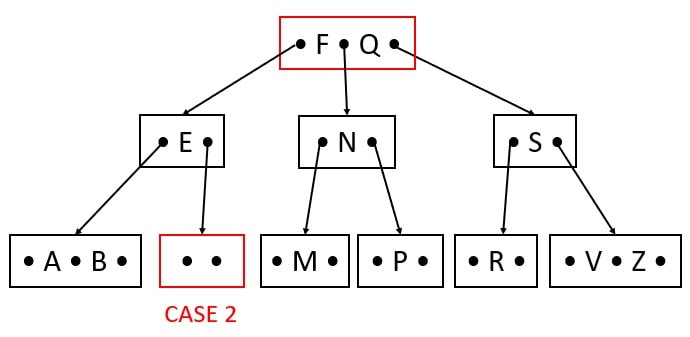
In Case 2, the deleted or replaced node can borrow a key from the left sibling.

Algorithm of deletion in b-tree

DeletionBTree(X,N,M)

Key to be deleted is X

Node which contains deleted key is N

Minimum degree is M

1. If Parent(N) = Nil //Root

        If Left(N) = Right(N) = Nil      //Root has no children

            Delete X

        Else Left(N) = Right(N) = Non-Nil   //Root have children

            Delete X and take the key from predecessor or successor.

2. Else, Parent(N) = Non-Nil

        If Left(N) = Right(N) = Nil      //Leaf node

            If N > M, delete X.

        Else If, N = M, delete X and take the key from predecessor or successor.

           If Predecessor = Successor = M, delete X and merge left sibling and minimum key of parent’s node.

        Else, Left(N) = Right(N) = Non-Nil      //Internal node

            Delete X and take the key from predecessor or successor.

                 If Predecessor = successor = M, merge them. 

. 

Time & Space Complexity of B-Tree

1. In searching, the time complexity is O(logn).
2. In insertion, the time complexity is O(logn).
3. In deletion, the time complexity is O(logn).
4. Space complexity is O(n).

Advantages of B-Tree

1. M-way tree is the index pages for huge random-access files.
2. Searching, Insertion and deletion operations are fast.
3. It can arrange large number of records in the less height of tree.
4. The tree has sorted order of keys.

Disadvantages of B-Tree

1. Insertion & deletion operations are complex.
2. When stored in RAM, B-trees are not as efficient as other balanced trees.

Applications of B-Tree

1. B-trees are used in databases and file systems to efficiently store and retrieve large amounts of data, optimizing disk access and minimizing search time.
2. They are employed in search engines to index web pages and quickly retrieve relevant results, improving the speed and efficiency of searches.
3. B-trees are used in file transfer protocols to organize and navigate directory structures, ensuring fast file access and transfer.
4. They find applications in database systems for indexing and querying multidimensional data, supporting efficient range searches and spatial queries.
5. B-trees are used in network routers to store routing tables and efficiently route data packets through complex networks, ensuring reliable and fast data transmission.
6. They are employed in transaction processing systems to manage large volumes of concurrent transactions, ensuring data integrity and high throughput.
7. B-trees find applications in file compression algorithms to organize and compress data efficiently, reducing storage space and improving file transfer speeds.
8. They are used in version control systems to manage revisions and branches of code repositories, facilitating efficient code collaboration and history tracking.