AVL Tree

AVL Tree was designed by Adelson-Velski and Landis in 1962. Thus, AVL represents the first letter of each originator’s first alphabet.

AVL tree is a self-balancing binary search tree. It balances the height of left subtree and right subtree. For each node, the height difference between the two subtrees is less than or equal to a predetermined value.

An AVL tree is called balanced when the difference of height is -1, 0, 1. It is also called balance factor (BF).

BALANCE FACTOR = Height of left subtree – Height of right subtree

.

How to check the height

1. Every leaf has balance factor 0.
2. Beginning at 0 from the leaves, the count will increase to the root.

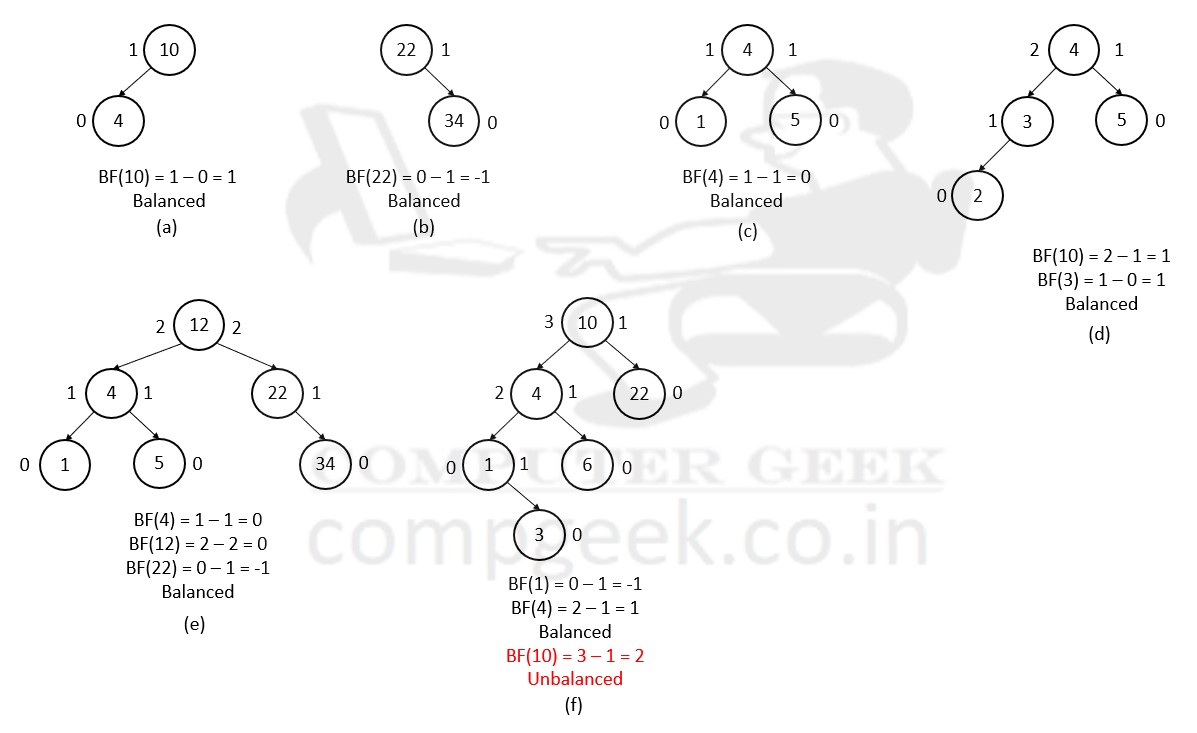
If the difference becomes more than 1 or less than -1, then we have to perform rotation to balance the height of subtrees.

.

There are four rotations possible in the AVL tree.

1) Left (LL ) rotation

2) Right (RR) rotation

3) Left Right (LR) rotation

4) Right Left (RL) rotation

.

(1) Left (LL) rotation

In this type of rotation, the new node is inserted to the left subtree of the left subtree.

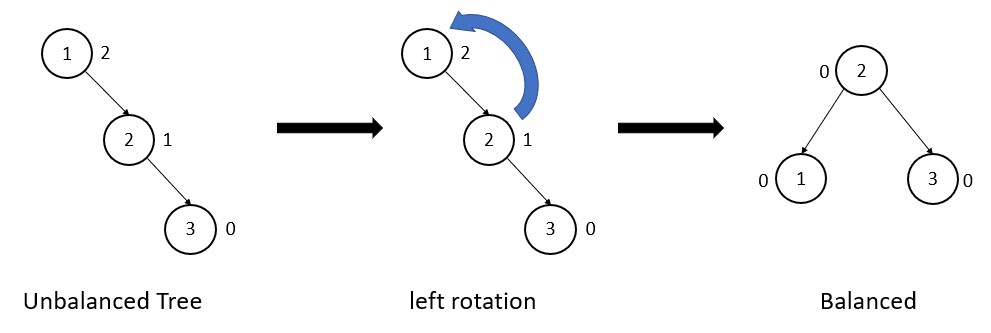
In this tree, node 1 has balance factor 2. As a result, the left rotation of node 1 makes this tree a balanced tree.

.

(2) Right (RR) rotation

In this type of rotation, the new node is inserted to the right subtree of the right subtree.

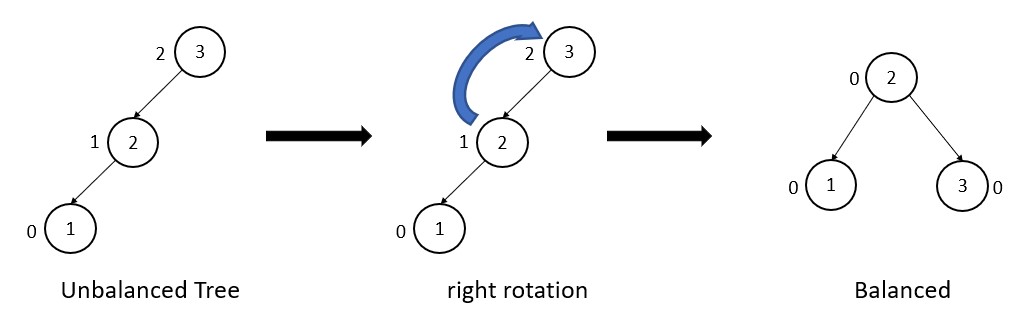
In this tree, node 3 has balance factor 2. As a result, the right rotation of node 3 makes this tree a balanced tree.

.

(3) Left-Right (LR) rotation

Left right rotation is difficult to understand, so you should concentrate first on the left rotation and then on the right rotation.

Suppose, the new node inserted on the right subtree of left subtree.

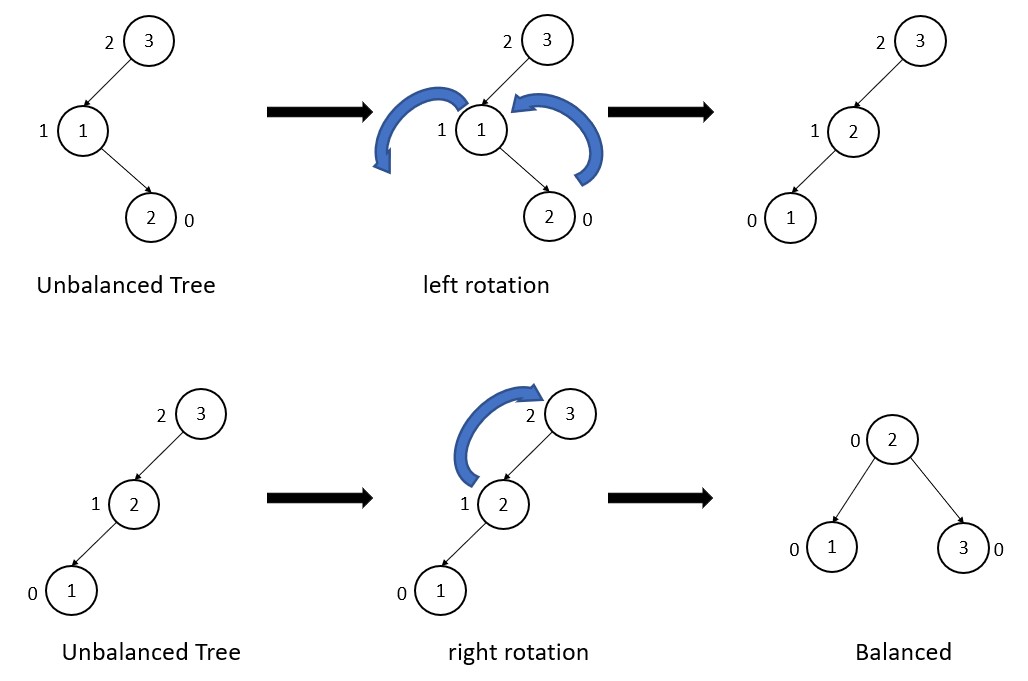
In this tree, node 3 of the unbalanced tree has a balance factor 2, but there is no left rotation or right rotation that node 3 can perform.

The binary search tree property must be preserved in the AVL tree, and rotation of node 3 violates this.

So, we perform node 1 and 2 rotation. After rotation, node 1 is leaf of the tree and node 2 is internal node of the tree.

After that, we perform right rotation of node 3.

.

(4) Right-Left (RL) rotation

Right-left rotation is difficult to understand, so you should concentrate first on the right rotation and then on the left rotation.

Suppose, the new node inserted on the left subtree of right subtree.

In this tree, node 1 of the unbalanced tree has a balance factor 2, but there is no left rotation or right rotation that node 1 can perform.

The binary search tree property must be preserved in the AVL tree, and rotation of node 1 violates this.

So, we perform node 3 and 2 rotation. After rotation, node 3 is leaf of the tree, and node 2 is internal node of the tree.

After that, we perform right rotation of node 1.

.

Working

Input is – {50, 12, 10, 72, 54, 95, 1, 52, 98}

.

Insert 50

The node 50 is inserted as a root in an empty tree.

.

Insert 12

The 12 is less than 50 (12 < 50), So it will be the left child of 50.  

12 has balance factor 0.

50 has balance factor 1.

So, Height is balanced.

.

Insert 10

The 10 is less than 12 (10 < 12), So it will be the left child of 12.

12 has balance factor 1.

50 has balance factor = 2 – 0 = 2.

By looking at the tree, we do right rotation.

As a result of rotation, 12 is the root. 10 is left child and 50 is right child of 12.

.

Insert 72

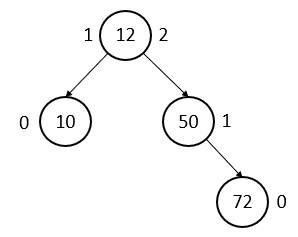
72 is greater than 50 (50 < 72), So it will be the right child of 50.

50 has balance factor -1.

12 has balance factor -1.

.

Insert 54

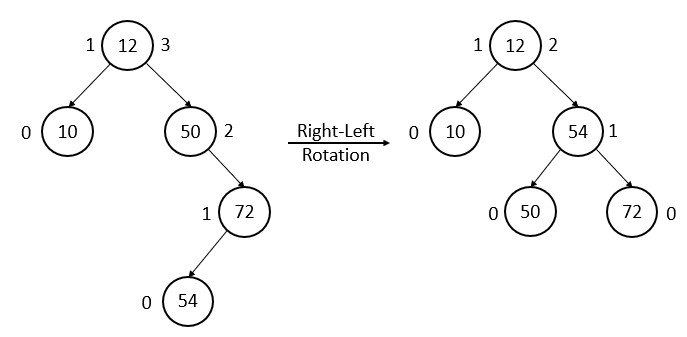
54 is less than 72 (54 < 72), So it will be the left child of 72.

72 has balance factor 1.

50 has balance factor -2.

We can overcome this problem by rotating node 50 to the left. However, 54 is already in the left position. Also, if 54 becomes the child with 50, we’ll have to go through another rotation. As a result, 54 and 72 will rotate to the right on the first rotation, whereas 50 will revolve to the left. We rotate (Right-Left).

As a result of rotations, 54 is the parent of 50 and 72.

.

Insert 95

95 is greater than 72 (95 > 72), So it will be the right child of 72.

72 has balance factor -1.

54 has balance factor -1.

12 has balance factor -2. So, we perform left rotation of 12.

.

Insert 1, 52

1 is less than 10 (1 < 10), So 1 will be the left child of 10.

52 is greater than 50 (52 > 50), So 52 will be the right child of 50.

12 has balance factor 0.

72 has balance factor -1.

54 has balance factor 1.

.

Insert 98

98 is greater than 95 (98 > 95), So 98 will be the right child of 95.

95 has balance factor -1.

54 has balance factor 0.

72 has balance factor -2. So, we perform left rotation of node 72.

As a result of rotation, 95 will be the parent of 72 and 98.

.

Insertion and deletion

Insertion and deletion in an AVL tree are conducted in the same manner as it is in a binary search tree. however still, it may cause a violation in the AVL tree property, requiring the tree to be rebalanced. Rotations can help balance the tree.

.

Time & Space Complexity of AVL Tree

Insertion, deletion and searching of a node in an AVL tree has a time complexity O(log n).

Insertion and deletion of the whole AVL tree has a time complexity O(n*log n).

Space Complexity of AVL tree is O(n).

.

Advantages of AVL Tree

1. The AVL tree is capable of self-balancing.
2. Due to the fact that the AVL tree is a height-balanced tree and n is the number of nodes in the tree, the height of the tree never increases over n.
3. Because the AVL tree is far more balanced, it is fast than the red-black tree.

Disadvantages of AVL Tree

1. Deletion operations in AVL trees are expensive because they need several pointer changes and rotations.

Applications of AVL Trees

1. AVL trees are like super-fast organizers for computers. They’re used in big databases to quickly find information you need, making searches lightning-fast.
2. AVL trees are like smart dictionaries for computers. They help them understand words (like variables and functions) in programming languages quickly and accurately.
3. Computers use AVL trees to tidy up messy folders and files. It’s like having a super organized filing cabinet where you can quickly find any document you need.
4. AVL trees are used to sort out tasks based on their importance. Imagine a to-do list where the most urgent tasks are always at the top, making it easy to know what to do next.