Asymptotic Notation (Hindi)

Design & Analysis of Algorithm

Asymptotic Notation

Introduction to Algorithm

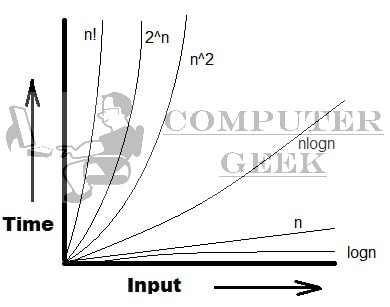
Growth of Function

Complexity को दिखाने के लिए हम एक approximation method ( अनुमानित तरीका ) प्रयोग में लाते है जिसको हम asymptotic notation भी बोलते है । यह approximate function के लिए एक error method की तरह है, मतलब कि काफी सारी अलगोरिथ्म्स कि Time Complexity हम सटीक (Accurate) नहीं निकाल सकते, हमारी counting में कुछ तो गड़बड़ होगी ही होगी, लेकिन हम ये बोल सकते है कि जो time complexity हमने निकली है वो जो अलगोरिथ्म कि real time complexity hai, उससे कम होगी, या ज़्यादा होगी, या फिर उसके इतनी निकट होगी कि हम फर्क न कर पाये । और यही हम Asymptotic Notation में सीखेंगे ।

एक example देखते हैं, यदि आपको “5n + 2n² + nlogn” की Time Complexity मिलती है, तो आपको 2n² पर ध्यान केंद्रित करना होगा क्यूंकी इसमे n कि value सबसे बड़ी है, बाकी 5n और nlogn को आपको नहीं रखना क्यूंकी ये lower-order term हैं | इसके बाद आपको 2n² में से भी 2 को भी निकाल देना होगा क्यूंकी ये एक constant term है। आपका answer n² होगा |

अल्गोरिथ्म को चलाने के लिए आवश्यक समय (Time), आवश्यक Storage (Space) की मात्रा, इसकी कुशलता तय करते हैं । अलगोरिथ्म कि कुशलता तय करने के लिए Asymptotic Notation का उपयोग किया जाता है। Input के प्रकार के आधार पर एक अल्गोरिथ्म का performance भिन्न हो सकता है। Important – Input का आकार बढ़ने पर performance बदल जाएगा।

	Asymptotic Notation	Symbol	Mathematical Nature
1	Big Oh	O	≤	Upper Bound – Worst Case सबसे खराब स्तिथि
2	Big Omega	Ω	≥	Lower Bound – Best Case सबसे अच्छी स्तिथि
3	Theta	Θ	=	Average Bound – Average Case (Exact Time)
4	Small oh	o	<
5	Small omega	ω	>

Big-Oh notation

= {f(n): there exist positive constants c and n₀, such that 0 ≤ f(n) ≤ g(n) for all n ≥ n₀}

g(n) is an asymptotic upper bound for f(n) for larger n (n ≥ no) c is a constant

मान लीजिए, g(n) उस अलगोरिथ्म कि सटीक (Exact) Time Complexity है | हमने उस अलगोरिथ्म कि Time Complexity निकाली जो f(n) आई, और हमको ये पता है कि g(n) upper bound है f(n) का। ये अलगोरिथ्म कम से कम f(n) time लेगी और ज्यादा से ज्यादा ये g(n) time में तो पूरी हो ही जाएगी चाहे कितनी भी परेशानी हो । तो g(n) time एक सबसे खराब स्तिथि है worst condition है जिसमे अलगोरिथ्म result दे देगी । g(n) = f(n) भी हो सकता है और f(n) से ज्यादा भी हो सकता है पर कम नहीं हो सकता।

अगर आपको अभी भी समझ नहीं आया तो एक example देता हूँ ।

मान लीजिए, अगर कोई लड़की किसी पार्टी के लिए तैयार होना चाहती है, तो आपको उसे आधे घंटे से ज्यादा का समय देना होगा। वो लगातार कहती है कि उसे तैयार होने के लिए केवल 10 मिनट की आवश्यकता है लेकिन वास्तविक समय 10 मिनट या 10 मिनट से अधिक होगा। हम जिस Time को calculate करते हैं वह g(n) होगा (जैसे की 5n² + 4n) और original time जो हम लिखते है वो f(n) होगा (जैसे की Big-Oh(n²) ) |

इसलिए हम ये कहेंगे कि f(n) = (Big-Oh) O(g(n))

Examples

1. If f(n) = 2n^2 and g(n) = n^3,

then what could be C and n_oif f(n) = O(C.g(n))

Ans. If C = 1 and n_o >= 2,

then 2n^2 = O(n^3)

Putting value, n_o = 2, 8 = 8

Putting value, n_o > 2, 2n^2 < n^3

2. If f(n) = 4n + 3 and g(n) = n,

then what could be C and n_oif f(n) = O(C.g(n))

Ans. If C = 5 and n_o >= 3,

then 4n + 3 = O(5n)

Putting value n_o = 3, 15 = 15

Putting value n_o > 3, 4n + 3 < 5n

3. If f(n) = 2n^3 + 6 then what is big-oh g(n)?

Ans. if g(n) is greater than or equal to f(n), then g(n) is big-oh of f(n).

2n^3 + 6 <= 2n^3 + 6n^3

<= 8n^3

so, f(n) = O(n^3) if C = 8 and n_o >= 1

Also, f(n) = O(n^3√n)/ O(n^4) / O(n^3 log n) for different values of C and n_o.

Big-Omega (Ω)

={f(n): there exist positive constants C and n_o, such that 0 ≤ C.g(n) ≤ f(n) for all n ≥n_o}

g(n) is an asymptotic lower bound for f(n) for larger n (n ≥ no)

मान लीजिए, आपने एक अलगोरिथ्म की Time Complexity n²निकाली पर आपको ये पता है अपने experience से की इस अलगोरिथ्म की time complexity n² होगी या n²से कम होगी। मगर आपको n की form मे ही answer देना है और आप nlogn भी नहीं लिख सकते क्यूंकी वो बहुत कम हो जाएगी तो आप n² ही लिखेंगे लेकिन आप एक symbol Ω लगाएंगे जो की best case को represent करेगा।

आपको एक और example देता हु, अगर कोई bachelor लड़का किसी पार्टी के लिए तैयार होना चाहता है, तो उसे तैयार होने के लिए मान लेते हैं कि 10 मिनट का समय दिया जाता है, लेकिन वह केवल 8-9 मिनट में तैयार हो जाता है, पर 10 मिनट की अधिकतम सीमा उसे जरूर मिलेगी। वह जो समय लेता है वह f(n) होगा (जैसे कि, n³) पर g(n) time होगा (n³ + 1)/2. यही कारण है कि f(n) >= C.g(n). इसके अलावा, f(n) = Ωg(n) के रूप में लिखा जा सकता है।

Examples

1. If f(n) = √n and g(n) = Log n,

then what could be C and n_oif f(n) = Ωg(n).

Ans. If C =1 and n_o= 16,

then, √n = Ω (log n)

Putting value n_o = 16, 4 = 4

Putting value n_o > 16, √n > (log n)

2. if f(n) = 2n^3, then what is big omega g(n)?

Ans.

2n^3 >= n^3

2n^3 >= n

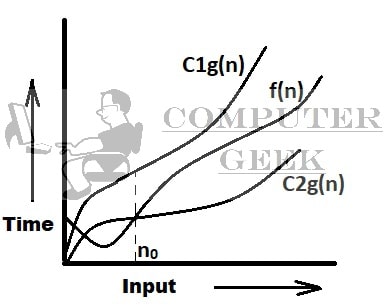
2n^3 >= √n and many more power of n which are less than or equal to 2n^3

Theta (Θ)

={f(n): there exist positive constants C1, C2 and n_o, such that 0 ≤ C1.g(n) ≤ f(n) ≤ C2.g(n) for all n ≥n_o}

g(n) is asymptotically tightly bound for f(n) for larger n (n ≥ no) It means Θ = O ∩ Ω

Example

1. If f(n) = (n^2)/2 – 2n and g(n) = n^2,

then what could be C1, C2 and n_oif f(n) = Θg(n)

Ans. C1 =1/4 C2 = 1/2 n_o= 8

=> 1/4 g(n) <= f(n) <= 1/2 g(n)

=> 1/4 (n^2) <= (n^2)/2 – 2n <= 1/2 (n^2)

by putting n_o= 8

=> 16 <= 16 <= 32

Small-Oh (o)

={f(n): there exist positive constants C and n_o, such that 0 ≤ f(n) < C.g(n) for all n ≥n_o}

Big-Oh और Small-oh के बीच एकमात्र अंतर यह है कि Big-Oh में f(n) ≤ C.g(n) है और small-oh में f(n) < C.g(n) है।

Examples

1. n^1.9999 = o (n^2)

2. n^2/ log n = o (n^2)

3. n^2 ≠o (n^2)

Small-Omega (ω)

={f(n): there exist positive constants C and n_o, such that 0 ≤ C.g(n) < f(n) for all n ≥n_o}

Big- Omega और Small- omega के बीच एकमात्र अंतर यह है कि Big- Omega में C.g(n) ≤ f(n) होता है और small-omega में C.g(n) < f(n) होता है।

Examples

1. n^2.0001 = ω(n^2)

2. n^2 log n = ω(n^2)

3. n^2 ≠ ω(n^2)

Design & Analysis of Algorithm