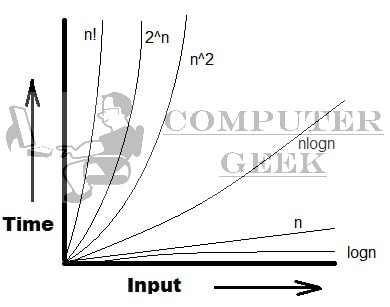
To represent complexity, there is an approximation method, which is also known as Asymptotic Notations. It is like an error method to approximate function means if you get an answer “5n + 2n^2 + nlogn”, then you have to focus on what’s important by abstracting away lower-order terms (like 5n, nlogn) and constant factors (like 2).
Paul Bachmann introduced the notation O(f(n)), Ω(f(n)), and Θ(f(n)) to describe the behavior of functions in terms of their growth rates. These notations, collectively known as asymptotic notation, have become fundamental tools in analyzing the complexity of algorithms and understanding the efficiency of computational processes. The amount of time, storage required to execute an algorithm, determine its efficiency. Asymptotic notations are used to calculate efficiency.
An algorithm’s performance may differ depending on the type of input. The performance will change as the input size increases.
| Asymptotic Notation | Symbol | Mathematical Nature | ||
| 1 | Big-Oh | O | ≤ | Upper Bound – Worst Case |
| 2 | Big-Omega | Ω | ≥ | Lower Bound – Best Case |
| 3 | Theta | Θ | = | Average Bound – Average Case (Exact Time) |
| 4 | Small-oh | o | < | |
| 5 | Small-omega | ω | > |
| 1. | Big-Oh (O) | = {f(n): there exist positive constants c and n0, such that 0 ≤ f(n) ≤ g(n) for all n ≥ n0} |

Let g(n) be the exact time complexity of the algorithm.
We have written the time complexity of the algorithm as f(n), and we know that g(n) is the upper bound of f(n). This algorithm execution will take at least f(n) time and at most, g(n) time, no matter how much easy problem is there. So, g(n) time is one of the worst conditions in which the algorithm will give results. g(n) time will be equal to the f(n) time or more than f(n) time but not less than f(n) time.
Suppose, if a girl wants to get ready for a party, then you have to give him more than half an hour. She continuously says that she requires only 10 minutes to get ready but the actual time will be 10 minutes or more than 10 minutes. The time we calculate will be g(n) (like, 5n2 + 4n), the original time to get ready is f(n) (like, Big-Oh(n2)).
Note – Sorry girls, I just wanted my readers to understand that what is Big-Oh.
Examples
1. If f(n) = 2n^2 and g(n) = n^3,
then what could be C and no if f(n) = O(C.g(n))
Ans. If C = 1 and no >= 2,
then 2n^2 = O(n^3)
Putting value no = 2, 8 = 8
Putting value no > 2, 2n^2 < n^3
2. If f(n) = 4n + 3 and g(n) = n,
then what could be C and no if f(n) = O(C.g(n))
Ans. If C = 5 and no >= 3,
then 4n + 3 = O(5n)
Putting value no = 3, 15 = 15
Putting value no > 3, 4n + 3 < 5n
3. If f(n) = 2n^3 + 6 then what is big-oh g(n)?
Ans. if g(n) is greater than or equal to f(n), then g(n) is big-oh of f(n).
2n^3 + 6 <= 2n^3 + 6n^3
2n^3 + 6 <= 8n^3
so, f(n) = O(n^3) if C = 8 and no >= 1
Also, f(n) = O(n^3√n)/ O(n^4) / O(n^3 log n) for different values of C and no.
| 2. | Big-Omega (Ω) | ={f(n): there exist positive constants C and no, such that 0 ≤ C.g(n) ≤ f(n) for all n ≥no} |

Assume you calculated an algorithm’s time complexity n2, but you already know from prior experience that the time complexity of this algorithm is less than n2. You must, however, respond in the form of n, and because nlogn is very little, you have to write n2, followed by the symbol Ω, which represents the best-case situation.
Another example is a bachelor boy who has 10 minutes to get ready for a party. However, he will be ready in 8-9 minutes, although the maximum time limit is 10 minutes. He will, of course, require g(n) (8-9 minutes) of time, but f(n) (10 minutes) will be written.
You can say that f(n) is n3 but g(n) time is (n3 + 1)/2. That is why f(n) >= C.g(n). Also, can be written as f(n) = Ωg(n).
Example
1. If f(n) = √n and g(n) = Log n, then what could be C and no if f(n) = Ωg(n).
Ans.
If C =1 and no = 16,
then, √n = Ω (log n)
Putting value no = 16, 4 = 4
Putting value no > 16, √n > (log n)
2. if f(n) = 2n^3, then what is big omega g(n)?
Ans.
2n^3 >= n^3
2n^3 >= n
2n^3 >= √n and many more which are less than or equal to 2n^3
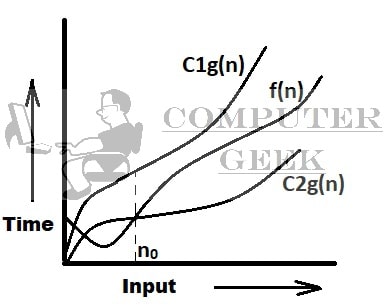
| 3. | Theta (Θ) | ={f(n): there exist positive constants C1, C2 and no, such that 0 ≤ C1.g(n) ≤ f(n) ≤ C2.g(n) for all n ≥no} |
Example
1. If f(n) = (n^2)/2 – 2n and g(n) = n^2,
then what could be C1, C2 and no if f(n) = Θg(n)
Ans.
C1 =1/4 C2 = 1/2 no = 8
-> 1/4 g(n) <= f(n) <= 1/2 g(n)
-> 1/4 (n^2) <= (n^2)/2 – 2n <= 1/2 (n^2)
by putting no = 8
-> 16 <= 16 <= 32
| 4. | Small-Oh (o) | ={f(n): there exist positive constants C and no, such that 0 ≤ f(n) < C.g(n) for all n ≥no} |
The only difference between Big-Oh and Small-oh is that Big-Oh has f(n) ≤ C.g(n) and small-oh has f(n) < C.g(n).
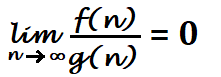
Examples
n^1.9999 = o (n^2)
n^2/ log n = o (n^2)
n^2 ≠o (n^2)

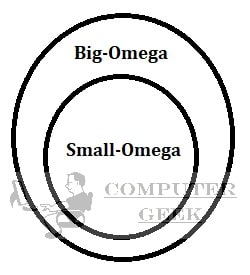
| 5. | Small-Omega (ω) | ={f(n): there exist positive constants C and no, such that 0 ≤ C.g(n) < f(n) for all n ≥no} |
The only difference between Big-Omega and Small-omega is that Big-Omega has C.g(n) ≤ f(n) and small-oh has C.g(n) < f(n).

Examples
n^2.0001 = ω(n^2)
n^2 log n = ω(n^2)
n^2 ≠ ω(n^2)
Properties of Asymptotic Notations
| Reflexive | Symmetric | Transitive | ||
|---|---|---|---|---|
| Big-Oh (O) | <= | ✓ | × | ✓ |
| Big-Omega (Ω) | >= | ✓ | × | ✓ |
| Small oh (o) | < | × | × | ✓ |
| Small omega (ꙍ) | > | × | × | ✓ |
| Theta (Θ) | = | ✓ | ✓ | ✓ |
Only for GATE & NET Aspirants
Reflexive property
Proof 1 – If f(n) is given, then prove f(n) = O(f(n))
Example – if f(n) = 3n2 + 4, then we have to prove that this f(n) = O(3n2 + 4)
Mathematical notation of Big-Oh is ‘<=’.
So, if you have any function of any type, we can say that the function is upper bound of itself. Because upper bound means ‘<=’, and the function is equal to itself. So, we can say that f(n) = O(f(n)).
Proof 2 – If f(n) is given, then prove f(n) = Ω(f(n)).
Ω is equal to ‘=>’, so we can say that a function is lower bound to itself, because the function is equal to itself.
Proof 3 – If f(n) is given, then prove f(n) = Θ(f(n)).
Θ is equal to ‘=’, so we can say that a function is tightly bound to itself, because the function is equal to itself.
Proof 4 – If f(n) is given, then prove f(n) ≠ o(f(n))
O is equal to ‘<’.
Here, no ‘=’ is given, so, we can say f(n) ≠ o(f(n))
And the same way, it is applied to f(n) ≠ ꙍ(f(n))
Symmetric Property
Proof 5 – If f(n) = Θ(g(n) is given, then prove g(n) = Θ(f(n)).
By the definition of Θ, there exists positive constants c1, c2, no such that c1.f(n) ≤ g(n) ≤ c2.f(n), for all n ≥ no
⇒ f(n) ≤ (1/c1).g(n) and f(n) ≥ (1/c2).g(n)
⇒ (1/c2).g(n) ≤ f(n) ≤ (1/c1).g(n)
According to the definition of, g(n) = (f(n))
This concludes the Symmetry property.
In every other asymptotic notation, less than or greater than property violates the symmetry.
Transitive Property
Proof 6 – If f(n) = O(g(n)) and g(n) = O(h(n)), then prove f(n) = O(h(n)).
According to the definition of Big-Oh(O), there exists positive constants c, no such that f(n) ≤ c.g(n), for all n ≥ no
⇒ f(n) ≤ c1.g(n)
⇒ g(n) ≤ c2.h(n)
⇒ f(n) ≤ c1.c2h(n)
⇒ f(n) ≤ c.h(n), where, c = c1.c2
This proves, f(n) = O(h(n))
Theta, omega, small-oh, small-omega satisfy the above property.
Test Yourself
Q1- Define Big-O notation and explain its significance in analyzing algorithm efficiency.
Big-O notation is used to describe the upper bound of an algorithm’s time complexity. It represents the worst-case scenario of an algorithm’s performance. By using Big-O notation, we can analyze and compare different algorithms to determine their efficiency and scalability.
Q2- What is the difference between Big-Omega and Big-Oh notations?
Big-Oh notation (O) represents the upper bound of an algorithm’s time complexity, while Big-Omega notation (Ω) represents the lower bound. Big-Oh describes the worst-case scenario, while Big-Omega describes the best-case scenario of an algorithm’s performance.
Q3- Explain the concept of Theta notation (Θ) and its significance.
Theta notation represents the tight bound of an algorithm’s time complexity. It provides both the upper and lower bounds, indicating the average case performance. It allows us to express the exact growth rate of an algorithm and is useful for analyzing algorithms with consistent behavior.
Q4- What does Small-Oh notation (o) indicate in terms of an algorithm’s time complexity?
Small-Oh notation represents a function that is strictly smaller than another function, indicating a faster growth rate. If f(n) = o(g(n)), it means that f(n) grows much slower than g(n) as n approaches infinity.
Q5- Describe Small-Omega notation (ω) and its relation to Big-Omega notation.
Small-Omega notation represents a function that is strictly greater than another function, indicating a slower growth rate. If f(n) = ω(g(n)), it means that f(n) grows much faster than g(n). Small-Omega is the inverse of Big-Omega notation.
Q6- Can a function be both Big-Oh and Big-Omega of another function simultaneously? Explain.
Yes, a function can be both Big-Oh and Big-Omega of another function simultaneously. If f(n) = Θ(g(n)), it means that f(n) has the same growth rate as g(n), implying that it is both an upper and lower bound for g(n).
Q7- Provide an example to demonstrate the reflexive property of Big-Oh notation.
Consider f(n) = 3n^2 + 4. The reflexive property states that f(n) = O(f(n)). In this case, f(n) is an upper bound of itself because it is equal to itself. Therefore, f(n) = O(f(n)).
Q8- Explain the symmetric property of asymptotic notations.
The symmetric property states that if f(n) = Θ(g(n)), then g(n) = Θ(f(n)). It means that if two functions have the same growth rate, they are interchangeable as upper and lower bounds.
Q9- Discuss the transitive property of asymptotic notations.
The transitive property states that if f(n) = O(g(n)) and g(n) = O(h(n)), then f(n) = O(h(n)). This property allows us to compare the time complexity of multiple functions and make conclusions about their growth rates.
Q10- How can asymptotic notations be used to compare the efficiency of different algorithms?
Asymptotic notations provide a standardized way to compare the performance of algorithms. By analyzing the upper and lower bounds of their time complexities, we can determine their growth rates and make informed decisions about which algorithm is more efficient for a given problem size.






