Analysis of algorithm defined in two ways. One is the time it takes, and the second is the space it takes.
Time Complexity:-
In computer science, time complexity is the number of operations done by the operating system from the start of the algorithm to the end of the algorithm.
Worst Case Complexity-
It is the maximum time taken by an algorithm to solve a problem.
Best Case Complexity-
It is the minimum time taken by an algorithm to solve a problem.
Average Case Complexity-
It is in between the best case and worst case.
This is the average time taken by an algorithm to solve a problem.
Space complexity:-
The amount of space or the number of bits required to solve a problem is referred to as its space complexity.
If we have two algorithms A1 and A2 for a problem. We want to know which one takes the least amount of time, we will count the time complexity of the algorithm. Our problem is not the space taken by that algorithm. In today’s world, space is unlimited. Our problem is the time. Time is valuable.
Time Complexity of a code
| Code | Number of Operations |
|---|---|
| int main() | 1 |
| { | 1 |
| int p = 1, sum = 0, n=10; | 1 |
for (p=1; p<=n; p++) { sum = sum + p; } | n |
| printf(sum); | 1 |
Sum of time complexity of different steps = 1 + 1 + 1 + n + 1
So, the time complexity is equal to n + 4
but we remove constant as constant will not play a big role in time complexity if n is so large.
Time Complexity of the code is O(n).
Analyze Complexities of Algorithm
There are multiple algorithms for a given problem. Assume we need to write a program to “swap the two numbers,” and we write two programs in C to do so. We are only looking at time complexity.
Code 1 – Swap(A,B,C)
- int main()
- {
- int A, B, C;
- printf(“Enter the first number : “);
- scanf(“%d”, &A);
- printf(“Enter the second number : “);
- scanf(“%d”, &B);
- C = A;
- A = B;
- B = C;
- printf(“After Swapping A : ”, A);
- printf(“After Swapping B : “, B);
Code 2 – Swap(A, B)
- int main()
- {
- int A, B;
- printf(“Enter two numbers : “);
- scanf(“%d %d”, &A, &B);
- A = A*B;
- B = A/B;
- A = A/B;
- printf(“After Swapping A : ”, A);
- printf(“After Swapping B : “, B);
As a result, code 1 swaps by using a variable C. The logic behind code 1 is that A and B are two numbers that we swap by putting the C variable value equal to the A variable value and A variable value equals B variable value. Now we will set the value of the B variable to the value of the C variable. As a result, A will become B, and B will become A.
This program includes no complex logic, only simple common sense. However, the space we used is a “int” data type variable.
In code 2, we swap values by not taking up space as we solve the problem internally. There are two variables A and B, and let’s say
A is equal to 3 and B is equal to 5.
We now multiply both variables and pass the result to variable A.
A = 15 and B = 5 as previously stated.
In the following step, we change the value of B to be equal to A/B, resulting in a new value of B of 3.
Now we must change the value of the A variable, which is equal to A/B, which equals 15/3 (the new value of B is 3), which equals 5. We swapped the values. B = 3 and A = 5.
The computer only understands addition. So, in code 2, if we multiply A and B, we must add A value to B times, which equals 5 + 5 + 5, and division requires more complex operations and time. The time complexity of code 2 will be greater than that of code 1.
If you take out the Time Complexity of both these codes, then the Time Complexity of both will be the same. Both are being solved in constant time but in reality, the time complexity of Code 2 will be more than that of Code 1. Because in code 2 we are doing more ‘number of operations’.
If we consider space complexity, code 2 is a good algorithm because it does not require more variables; however, if we consider time complexity, code 1 will be executed in less time than code 2.
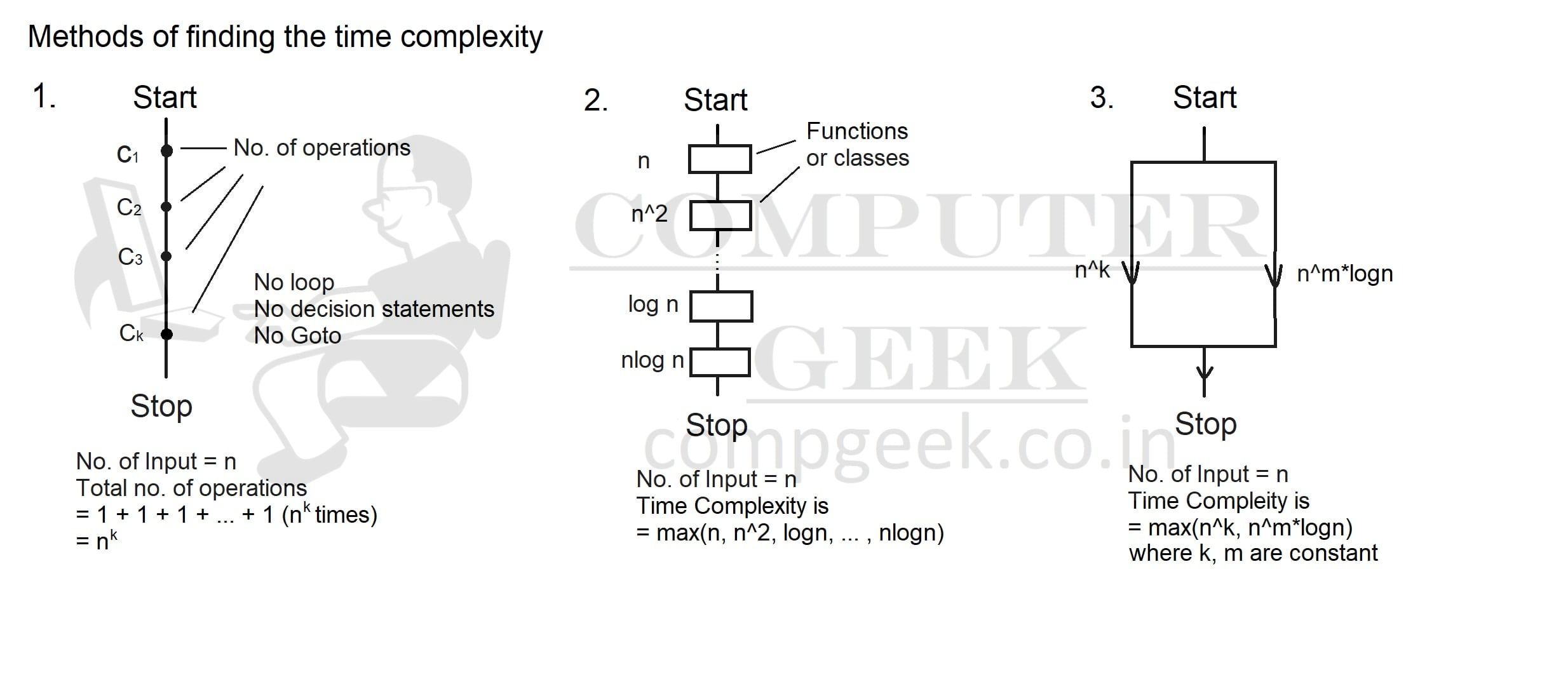
Find the time complexity of algorithm (Important)
We know that time complexity is actually the number of operations and those operations will be that are more will be time complexity. Our code or algorithm is in a sequence and mostly contains decision statements that are based on a condition. If the condition is true, one statement will be compiled and if the condition is false, then the other statement will execute. There are also some loops such as for loop and while loop and their time complexity are based on some conditions. There is a recurrence theorem that we will read in the future lessons and discuss the time complexity.

Test Yourself
Q1- Find the time complexity of code-
(A)
for (i = 1; i <= n; i++)
{
printf(“Hello”);
}
Time Complexity: is number of operations
In this code, I will take the value of i from 1 to n.
i = 1, print “hello”
i = 2, print “hello”
i = 3, print “hello”
…
…
i = n, print “hello”
i = n+1, condition becomes false
So, the code will print “hello” exactly n times and the time complexity is n+1. We remove the constant term and apply Big-Oh symbol. So, the Time complexity is O(n)
(B)
for(i = 1; i <= n; i++)
{
for(j = 1; j <= n; j++)
{
printf(“Hello”);
}
}
In this code,
i | j |
1 | 1, 2, 3, ……, n |
2 | 1, 2, 3, ……, n |
3 | 1, 2, 3, ……, n |
….. | …… |
….. | …… |
n | 1, 2, 3, ……, n |
means it will print “hello” for every j value.
so j value is 1 to n, for every ith value. i value is from 1 to n.
so, we have n*n operations. Time Complexity is O(n^2).
Note- Time complexity is Number of operations. So, j value is going to be from 1 to n+1. In n+1, its j value is false. Also, i value is going from 1 to n+1. So what i mean to say is that time complexity is (n+1)^2. But according to our rules, lower order term and constants are discarded. That is why, time complexity is O(n^2).
(C)
for(i = 1; i <= n; i++)
{
for(j = 1; j <= i; j++)
{
printf(“Hello”);
}
}
In this code
i | j |
1 | 1 |
2 | 1, 2 |
3 | 1, 2, 3 |
….. | …… |
….. | …… |
n | 1, 2, 3, ……, n |
means it will print “hello” for every j value.
so, j values sum equal to
Sum = 1 + 2 + 3 + … + n = (n(n+1))/2
Sum = (n^2 + n)/2 = O(n^2) (We remove constants and lower-order term.)
(D)
for(i = 1; i <= n; i++)
{
for(j = 1; j<= n; j = j*2)
{
printf(“Hello”);
}
}
In this code,
i | j |
1 | 1, 2, 4, …, k |
2 | 1, 2, 4, …, k |
3 | 1, 2, 4, …, k |
….. | …… |
….. | …… |
n | 1, 2, 4, …, k |
2^k <= n
After every j’s value, the code will print “hello”.
so, # of operations is n*k [k = log n]
It means that time complexity is O(n log n).
(E)
for(i = 0; i <= n; i = i*2)
{
for(j = 0; j <= n; j = j*2)
{
printf(“Hello”);
}
}
In the previous question, we have seen that j = j*2 derives time complexity log n.
So, in this question, i value is from 1 to n and i = i*2, and in the nested loop j value is from 1 to n and j = j*2.
So, the code’s time complexity becomes O((log n)^2).
Q2- If we have two algorithms for a problem Algo1 & Algo2. Algo1 has time complexity of O(n) and has a space complexity of O(n). Algo2 has a time complexity of O(n*logn) and has a space complexity of O(1). Which algorithm will you choose?
Generally, we do not think about space. We only think about time. Algorithm has to be time-effective. Algo1 has time complexity O(n) which is less than the time complexity of algo2 O(n*logn). So, we will use Algo1.
Suppose there is an old version of a software in your laptop, and it uses very less space but time complexity is higher in comparison to a new version of the same software. But new version wants a higher space than the old version. What will you choose? Ultimately you will buy a new laptop with 1TB or 2TB space and has a RAM of 8GB or higher, and install the new version which costs you less time.
Note- If you want a space-efficient algorithm, you choose Algo2. But this will happen only in less cases.






