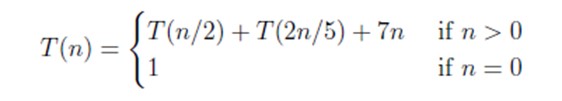Design & Analysis of Algorithm logo

Algorithm Questions Answers GATE 2021

Prev
NEXT
Menu

Design & Analysis of Algorithm GATE Question Answers with Explanation.

SET 1

Q1 – Let P be an array containing n integers. Let t be the lowest upper bound on the number of comparisons of the array elements, required to find the minimum and maximum values in an arbitrary array of n elements. Which one of the following choices is correct? (GATE 2021 Set 1)
  1. t > 2n – 2
  2. t > 3.ceil(n/2) and t ≤ 2n – 2
  3. t > n and t ≤ 3.ceil(n/2)
  4. t > ceil(log2n) and t ≤ n

Ans – (3)

Explanation –

Q2 – Consider the following three function.
       f1 = 10n      f2 = nlogn     f3 = n√n
Which one of the following options arranges the functions in the increasing order of asymptotic growth rate? (GATE 2021 Set 1)

 

  1. f3, f2, f1
  2. f2, f1, f3
  3. f1, f2, f3
  4. f2, f3, f1

Ans – (4)

Explanation –

Q3 – Consider the following array.

Algorithm Q9 GATE 2021 Set 1

Which algorithm out of the following options uses the least number of comparisons (among the array elements) to sort the above array in ascending order? (GATE 2021 Set 1)

 

  1. Selection Sort
  2. Merge Sort
  3. Insertion Sort
  4. QuickSort using the last element as pivot.

Ans – (3)

Explanation – 

Q4 – A binary search tree T contains n distinct elements. What is the time complexity of picking an element in T that is smaller than the maximum element in T? (GATE 2021 Set 1)
  1. ÆŸ(nlogn)
  2. ÆŸ(n)
  3. ÆŸ(logn)
  4. ÆŸ(1)

Ans – (4)

Explanation –

Q5 – Consider the following recurrence relation.  
GATE 2021 Set 1
Which one of the following options is correct? (GATE 2021 Set 1)
  1. T(n) = Θ(n5/2)
  2. T(n) = Θ(nlogn)
  3. T(n) = Θ(n)
  4. T(n) = Θ((logn)5/2)

Ans – (3)

Explanation –

Q6 – Define Rn to be the maximum amount earned by cutting a rod of length n meters into one or more pieces of integer length and selling them. For i>0, let p[i] denote the selling price of a rod whose length is i meters. Consider the array of prices:
p[1]=1, p[2]=5, p[3]=8, p[4]=9, p[5]=10, p[6]=17, p[7]=18
Which of the following statements is/are correct about R7? (GATE 2021 Set 1)
  1. R7 = 18
  2. R7 = 19
  3. R7 is achieved by three different solutions
  4. R7 cannot be achieved by a solution consisting of three pieces.

Ans – (1, 3)

Explanation –

Q7 – An articulation point in a connected graph is a vertex such that removing the vertex and its incident edges disconnects the graph into two or more connected components.
Let T be a DFS tree obtained by doing DFS in a connected undirected graph G. Which of the following options is/are correct? (GATE 2021 Set 1)

 

  1. Root of T can never be an articulation point in G.
  2. Root of T is an articulation point in G if and only if it has 2 or more children.
  3. A leaf of T can be an articulation point in G.
  4. If u is an articulation point in G such that x is an ancestor of u in T and y is a descendent of u in T, then all paths from x to y in G must pass through u.

Ans – (2)

Explanation –

Q8 – Consider the following Boolean expression.
F=(X+Y+Z)(X’+Y)(Y’+Z)
Which of the following Boolean expressions is/are equivalent to F’ (complement of F)? (GATE 2021 Set 1)
  1. (X’+Y’+Z’)(X+Y’)(Y+Z’)
  2. XY’+Z’
  3. (X+Z’)(Y’+Z’)
  4. XY’+YZ’+X’Y’Z’

Ans – (2, 3, 4)

Explanation –

Prev
NEXT
GATE Syllabus
GATE Previous Year Paper
MCQs of Algorithm