Design & Analysis of Algorithm GATE Question Answers with Explanation.
Q1 – Which one of the following statements is TRUE for all positive functions f(n)? (GATE 2022)
1. f(n2) = Ɵ(f(n)2), when f (n) is a polynomial
2. f(n2) = o(f(n)2)
3. f(n2) = O(f(n)2), when f (n) is an exponential function
4. f(n2) = Ω(f(n)2)
Ans – (1)
Explanation – To analyze the given options:
(1) f(n^2) = Θ(f(n)^2), when f(n) is a polynomial
This statement is true.
Comparing f(n^2) and f(n)^2, we can see that they have the same form, but with different coefficients. Therefore, we can conclude that f(n^2) = Θ(f(n)^2) when f(n) is a polynomial. Hence, option (1) is true.
(2) f(n^2) = o(f(n)^2)
This statement is not necessarily true. The little-o notation represents a function that grows faster than another function. While it may be true for specific functions, it is not universally true for all positive functions f(n). Therefore, option (2) is false.
(3) f(n^2) = O(f(n)^2), when f(n) is an exponential function
This statement is not necessarily true. An exponential function grows much faster than a polynomial function. Therefore, it cannot be guaranteed that f(n^2) = O(f(n)^2) when f(n) is an exponential function. Hence, option (3) is false.
(4) f(n^2) = Ω(f(n)^2)
This statement is not necessarily true. The big-omega notation represents a function that grows at least as fast as another function. While it may be true for specific functions, it is not universally true for all positive functions f(n). Therefore, option (4) is false.
Q2 – Consider a simple undirected weighted graph G, all of whose edge weights are distinct. Which of the following statements about the minimum spanning trees of G is/are TRUE? (GATE 2022)
1. The edge with the second smallest weight is always part of any minimum spanning tree of G.
2. One or both of the edges with the third smallest and the fourth smallest weights are part of any minimum spanning tree of G.
3. Suppose S ⊆ V be such that S ≠ Φ and S ≠ V. Consider the edge with the minimum weight such that one of its vertices is in S and the other in V \ S . Such an edge will
always be part of any minimum spanning tree of G.
4. G can have multiple minimum spanning trees.
Ans – (1, 2, 3)
Explanation –
Because there is only one MST, these previous statements may be stated as “The edge with the second smallest weight is always part of the minimum spanning tree of G.”
The “Kruskal Algorithm” can be used to determine MST. Kruskal Algorithm will add the Minimum Edge and Second Minimum Edge to the MST. Option 1 is correct.
One or both of the edges with the third smallest and the fourth smallest weights are part of any minimum spanning tree of G.
This statement is true. In any minimum spanning tree, the edges with the third and fourth smallest weights will be included. This can be proved using a contradiction argument. If both of these edges were excluded from the minimum spanning tree, we could replace an existing edge with a smaller one, contradicting the minimality of the spanning tree.
Therefore, Option 2 is correct.
The option 3 is true. This is known as the cut property of minimum spanning trees. In any minimum spanning tree, the edge with the minimum weight that crosses the cut between S and V \ S will always be included. This can be proven using a similar contradiction argument as in statement 2.
G can have multiple minimum spanning trees: False (Because all edge weights are distinct). So, option 4 is incorrect.
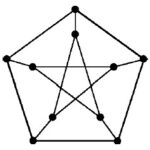
Q3 – The following simple undirected graph is referred to as the Peterson graph.
Which of the following statements is/are TRUE? (GATE 2022)
1. The chromatic number of the graph is 3.
2. The graph has a Hamiltonian path.
3. The following graph is isomorphic to the Peterson graph.
4. The size of the largest independent set of the given graph is 3. (A subset of vertices of a graph form an independent set if no two vertices of the subset are adjacent.
Ans – (1, 2, 3)
Explanation –
Option 1 is correct because the minimum number of colours necessary for this graph is 3.
Rule 1 – First, colour the vertices with the highest degree.
Rule 2 – Fill the vertex with the chosen colour if it isn’t already present on the neighbouring vertex.
Option 2 is also correct because your Hamiltonian path has a starting vertex that is also your ending vertex.
Option 3 is also correct. The provided graphs will have an equal number of vertices. The provided graphs will have an equal number of edges. The provided graphs will have an equal number of degree sequences.
Option 4 is incorrect. The size of the graph’s largest independent collection is 3. If no two of the subset’s vertices are nearby, they constitute an independent set and are referred to as subsets of vertices.
Q4 – Consider the following recurrence:
f(1) = 1;
f(2n) = 2f(n) – 1, for n ≥ 1;
f(2n + 1) = 2f(n) + 1, for n ≥ 1;
Then, which of the following statements is/are TRUE? (GATE 2022)
1. f (2n – 1) = 2n – 1
2. f (2n) = 1
3. f (5.2n) = 2n+1 + 1
4. f (2n + 1) = 2n + 1
Ans – (1, 2, 3)
Explanation – In this question, we have to find the output based on n value.
Equation 1, f(1) = 1,
Equation 2, f(2n) = 2f(n) – 1, for n ≥ 1;
This is for the value of even numbers.
It has a further classification that if the number is 2n, its value is always 1.
f(2) = 2*f(1)-1 = 1
f(4) = 2*f(2)-1 = 1
f(8) = 2*f(4)-1 = 1
f(16) = 2*f(8)-1 = 1
So, option 2 is correct.
Also, you can check other even numbers such as
f(6) = 2*f(3)-1 = 5
f(10) = 2*f(5)-1 = 5
f(12) = 2*f(6)-1 = 9
f(14) = 2*f(7)-1 = 13
Equation 3, f(2n + 1) = 2f(n) + 1, for n ≥ 1;
This is for the value of odd numbers.
It has a further classification that if the number is 2n-1, its value is always 2n-1.
When n=1, f(3) = f(4-1) = 2*f(1)+1 = 3
When n=3, f(7) = f(8-1) = 2*f(3)+1 = 7
When n=7, f(15) = f(16-1) = 2*f(7)+1 = 15
So, option 1 is correct.
Option 3 – f(5.2n) = 2n+1 + 1
When n = 0, f(5) = 3 and it is correct by equation 3.
When n = 1, f(10) = 5 and it is correct by equation 2.
When n = 2, f(20) = 9 and it is correct by equation 2.
So, option 3 is correct.
Option 4 – f(2n+1) = 2n + 1
When n = 0, f(2) = 2 and it is incorrect by equation 2.
So, option 4 is incorrect.
Q5 – Which of the properties hold for the adjacency matrix A of a simple undirected unweighted graph having n vertices? (GATE 2022)
1. The diagonal entries of A2 are the degrees of the vertices of the graph.
2. If the graph is connected, then none of the entries of An-1 + In can be zero.
3. If the sum of all the elements of A is at most 2(n – 1), then the graph must be acyclic.
4. If there is at least a 1 in each of A’s rows and columns, then the graph must be connected.
Ans – (1)
Explanation –
Option 1 –
Let A be the adjacency matrix of the graph. The entry Aij of A^2 represents the number of paths of length 2 between vertices i and j. Since the graph is simple and undirected, each entry Aii of A^2 counts the number of paths of length 2 starting and ending at vertex i, which is equal to the degree of vertex i. Therefore, this statement is true.
Option 2 –
This statement is not true. For a connected graph, the sum of the entries in each row of A^(n−1) (excluding the diagonal) represents the number of paths of length n−1 starting from that vertex. However, it’s possible for some entries to be zero even in a connected graph.
Option 3 –
This statement is not true. The sum of the entries of A represents the total number of edges in the graph. For a graph with n vertices, the maximum number of edges in an undirected graph is n(n−1)/2, which is achieved in a complete graph. This sum can exceed 2(n−1) even for acyclic graphs.
Option 4 –
This statement is also not true. Having at least one 1 in each row and column of A means that every vertex is adjacent to at least one other vertex. However, this condition is not sufficient to guarantee connectivity. There could still be isolated components in the graph.
Q6 – Let G(V , E) be a directed graph, where V = {1, 2, 3, 4, 5} is the set of vertices and E is the set of directed edges, as defined by the following adjacency matrix A.
𝐴[𝑖][𝑗] = 1, 1 ≤ 𝑗 ≤ 𝑖 ≤ 5
𝐴[𝑖][𝑗] = 0, 𝑜𝑡ℎ𝑒𝑟𝑤𝑖𝑠𝑒
𝐴[𝑖][𝑗] = 1 indicates a directed edge from node i to node j. A directed spanning tree of G, rooted at r ϵ V, is defined as a subgraph T of G such that the undirected version of T is a tree, and T contains a directed path from r to every other vertex in V. The number of such directed spanning trees rooted at vertex 5 is_____________. (GATE 2022)
Ans – (24) (Twenty Four)
Explanation – There are 5 vertices and if 5 to 1 is an edge directed at 1 then there can’t be an edge from 1 to 5 directed at 5.
So, we have to make a directed spanning tree. So, we have to make permutation of edges in 5 vertices.
First vertex have 4 other vertices to make an edge. Similarly, Second vertex have 3 other vertices to make an edge and so on.
Permutation is 4*3*2*1 = 24 Trees are there which can be built.