Unit 6
Dynamic Programming:- All Pair Shortest Path – Warshal’s and Floyd’s Algorithms, Resource Allocation Problem. Backtracking, Branch & Bound, Travelling Salesman Problem, Graph Coloring, N-Queen Problem, Hamiltonian Cycles, Sum of Subsets, Longest Common Subsequence.
University Questions are from
(AKTU, IPU, DTU, MDU, LPU, VIT, SRM, Amity, PU, JMI and many more…)
Design & Analysis of Algorithm
Assignment 1
Q – What steps are used in Dynamic Programming Approach? Discuss the 0/1 Knapsack problem with respect to dynamic programming. Is greedy method equally applicable for the above problem?
Q – Discuss backtracking problem solving approach with the help of an example.
Q – What do you mean by branch & bound? How TSP can be solve using this approach.
Q – Discuss n queen’s problem. Solve 4 queen’s problem using backtracking method?
Q – Prove that three colouring problem is NP complete.
Design & Analysis of Algorithm
Assignment 2
Q – What is travelling salesman problem? Find the solution of following travelling salesman problem using branch and bound method.
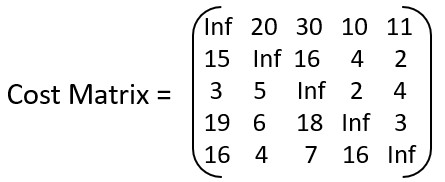
Q – Write pseudocode for 8 queen problem.
Q – What is the running time complexity of 8 queen’s problem?
Q – Write down an algorithm to compute Longest Common Subsequence (LCS) of two given strings and analyze its time complexity.
Q – Write an algorithm for sum subset problem using back tracking approach. Find all possible solution for following instance using same if m = 30, S = <1, 2, 5, 7, 8, 10, 15, 20, 25 >.
Design & Analysis of Algorithm
Assignment 3
Q – Develop a dynamic programming algorithm to evaluate nck where nck = n!/(k!*(n-k)!)
Q – The sum of subsets problem is to find all combinations of the n given distinct numbers whose sum is M. Draw the state space tree for the problem with numbers 7, 5, 12, 18, 20, 8 and M = 25.
Q – Develop an analyse an algorithm to determine whether a given NxN matrix A has the metric property (that is, for all values of 1≤i, j, k≤N, aij ≤ aik + akj) or not.
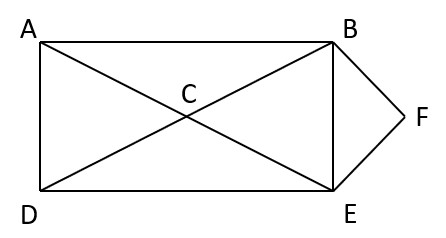
Q – Find the Hamiltonian circuit in the following graph using backtracking.
Q – Show how to compute transitive closure of a graph using Floyd-Warshell’s algorithm for all pairs shortest paths.
Design & Analysis of Algorithm
Assignment 4
Q – Give a recursive solution to travelling sales person problem.
Q – Explain Floyd-Warshall algorithm with suitable example.
Q – When and how Dynamic Programming approach is applicable? Discuss the matrix chain multiplication with respect to dynamic programming technique.
Q – What is backtracking? Write general iterative algorithm for backtracking.
Q – What is graph coloring problem? What do you mean by optimally coloring of a graph? Show that every bipartite graph is 2-colorable.
Design & Analysis of Algorithm
Assignment 5
Q – Define Dynamic programming. How dynamic programming approach is used to find the shortest path? Illustrate with an example.
Q – Give a dynamic programming solution for the subset sum problem. Analyze the complexity of the algorithm.
Q – Define different complexity classes in detail with suitable example. Show that problem is NP complete.
Q – What is backtracking? Discuss sum of subset problem with the help of an example.
Q – Discuss n queen’s problem. Solve 4 queen’s problem using backtracking method?
Design & Analysis of Algorithm
Assignment 6
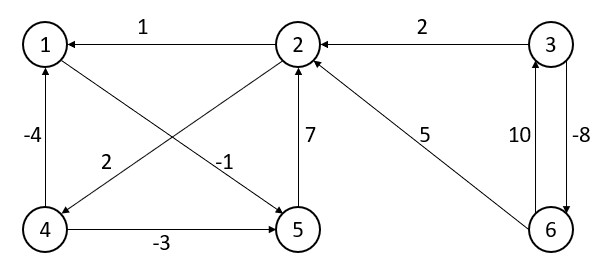
Q – For the graph (Weighted, directed) apply Floyd-Warshall algorithm for constructing shortest path. Show the matrix Dk that results each iteration.
Q – Discuss Travelling salesman Problem and various approaches to solve the problem with complexity analysis of each.
Q – Show that a TSP can be solved using backtracking method in the exponential time.
Q – Discuss the dynamic programming solution to longest common subsequence (LCS) problem. Write an algorithm to compute an LCS of two given strings.
Q – Write Short notes on the following.
(i) Graph Coloring
(ii) Hamiltonian cycles
(iii) N-queen problem
Design & Analysis of Algorithm
Assignment 7
Q – Illustrate the applications of graph coloring problem.
Q – Write Short notes on the following.
(i) Hamiltonian cycles
(ii) N-queen problem
Q – What is the sum of subsets problem? Let w = {5, 7, 10, 12, 15, 18, 20} and m = 35. Find all possible subsets of w that sum to m using recursive backtracking algorithm for it. Draw the portion of the state space tree that is generated.
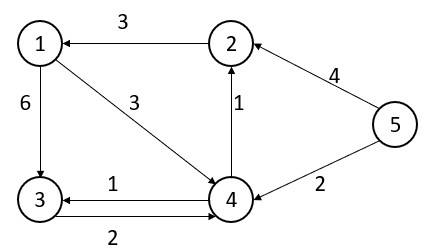
Q – Define Floyd Warshall Algorithm for all pair shortest path and apply the same on the following graph:
Q – Define TSP problem in detail. Find the solution for the following instance of TSP problem using branch and bound.
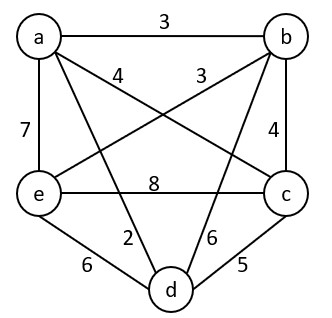
Design & Analysis of Algorithm
Assignment 8
Q – Write is sum of subset problem? Draw a state space tree for Sum of subset problem using backtracking? Let n=6, m=30 and w[1:6] = {5, 10, 12, 13, 15, 18}.
Q – Find an LCS for the sequences, X = {x1, x2, …, xm} and Y = {y1, y2, …, yn}. Also show that it requires O(m+n) time.
Q – Write Short notes on the following. **
(i) Graph Coloring
(ii) Hamiltonian cycles
(iii) N-queen problem
Q – What steps are used in Dynamic Programming Approach? Discuss the 0/1 Knapsack problem with respect to dynamic programming. Is greedy method equally applicable for the above problem?
Q – Develop a dynamic programming algorithm to evaluate nck where nck = n!/(k!*(n-k)!)
Design & Analysis of Algorithm
Assignment 9
Q – Differentiate between Dynamic Programming and Greedy approach. What is 0/1 knapsack problem? Solve the following instance using dynamic programming. Write the algorithm also. Knapsack Capacity = 10, P = <1, 6, 18, 22, 28> and w = <1, 2, 5, 6, 7>.
Q – What is travelling salesman problem? Find the solution of following travelling salesman problem using branch and bound method.
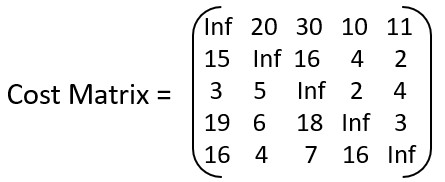
Q – Find the Hamiltonian circuit in the following graph using backtracking.

Q – Explain Floyd-Warshall algorithm with suitable example.
Q – Solve the following 0/1 knapsack problem using dynamic programming. P = [11, 21, 31, 33], w = [2, 11, 22, 15], c = 40, n =4.
Q – Differentiate between backtracking and branch and bound approach.

