Unit 5
Greedy Method:- Optimal Reliability Allocation, Fractional Knapsack, 0/1 Knapsack, Minimum Spanning Tree:- Prim’s Algorithm, Kruskal’s Algorithm, Single Source Shortest Path:- Dijkstra’s and Bellman Ford Algorithm, Graph – BFS, DFS. Topological Sort.
University Questions are from
(AKTU, IPU, DTU, MDU, LPU, VIT, SRM, Amity, PU, JMI and many more…)
Design & Analysis of Algorithm
Assignment 1
Q – Define principle of optimality.
Q – What are greedy algorithms? Explain their characteristics?
Q – Explain Dijkstra’s algorithm to solve single source shortest path problem with suitable example.
Q – Find optimal solution to the fractional knapsack instances n=7 and knapsack capacity M=15 where profits and weights are as follows (p1, p2, … p7) = (10, 5, 15, 7, 6, 18, 3) & (w1, w2, … w7) = (2, 3, 5, 7, 1, 4, 1) respectively.
Q – Difference between Greedy Technique and Dynamic Programming.
Design & Analysis of Algorithm
Assignment 2
Q – Describe Huffman’s algorithm with an example for generation for prefix code.
Q – What are strongly connected components? Write about articulation points in a graph.
Q – Show how Prim’s algorithm can be implemented using heap. What would be the time complexity of an algorithm?
Q – Prove the correctness of Kruskal’s algorithm.
Q – Give an algorithm for topological sorting of a directed acyclic graph.
Design & Analysis of Algorithm
Assignment 3
Q – Any greedy approach to an activity selection problem of scheduling several competing activities that require exclusive use of common resources, with a goal of selecting a maximum size set of mutually compatible activities.
Q – Prove that if the weights on the edge of the connected undirected graph are distinct then there is a unique Minimum Spanning Tree. Give an example in this context. Also, discuss Kruskal’s minimum spanning tree in detail.
Q – Given a graph G = (V1, E) and let V1 and V be two distinct vertices. Explain how to modify Dijkstra’s shortest path algorithm to determine the number of distinct shortest paths from U to V. Also, comment on whether Dijkstra’s shortest path algorithm work correctly if weights are negative.
Q – What is an optimization problem? How are greedy method can be used to solve the optimization problem?
Q – Write an algorithm to find shortest path between all pairs of nodes in a given graph.
Design & Analysis of Algorithm
Assignment 4
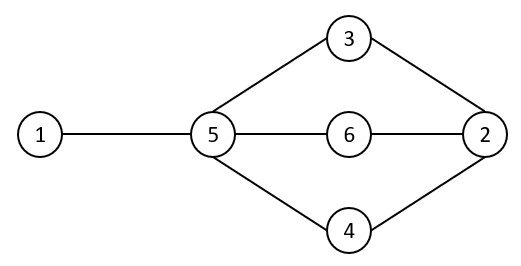
Q – What is “Greedy algorithm”? Write its pseudocode. Apply greedy algorithm on coloring the vertices of the following graph:
Q – Define spanning tree. Write kruskal’s algorithm for finding the minimum cost spanning tree. Describe how kruskal’s algorithm is different from prim’s algorithm for finding the minimum cost spanning tree.
Q – prove that if the weights on the edge of the connected undirected graph are distinct then there is a unique minimum spanning tree. Give an example in this regard. Also discuss Prim’s minimum spanning tree algorithm in detail.
Q – In the previous question, Also, discuss Kruskal’s minimum spanning tree in detail.
Q – Write Short note on Dijkstra’s algorithm shortest path problem.
Design & Analysis of Algorithm
Assignment 5
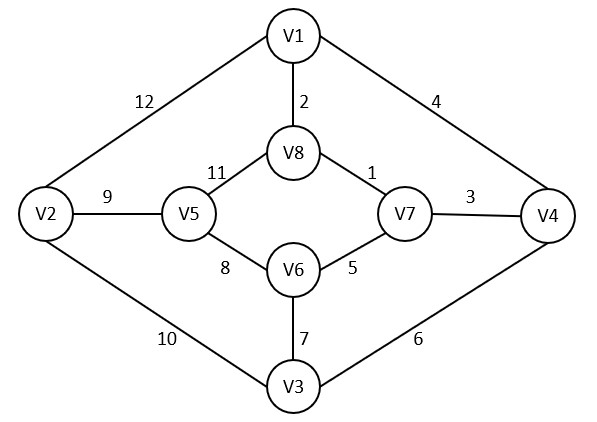
Q – Define minimum cost spanning tree. Write Prim’s algorithm to generate a minimum cost spanning tree for any given weighted graph. Generate minimum cost spanning tree for the following graph using Prim’s algorithm.
Q – Explain and write an algorithm for greedy method of algorithm design. Given 10 activities along with their start and finish time as
S = {A1, A2, A3, A4, A5, A6, A7, A8, A9, A10}
Start time = {1, 2, 3, 4, 7, 8, 9, 9, 11, 12}
Finish time = {3, 5, 4, 7, 10, 9, 11, 13, 12, 14}
Compute a schedule where the largest numbers of activities take place.
Q – Given the six items in the table below and a knapsack with weight 100. What is the solution to the knapsack problem in all concept. Explain greedy all approaches and find the optimum solution.
Item id | Weight | Value | Value/Weight |
A | 100 | 40 | 0.4 |
B | 50 | 35 | 0.7 |
C | 40 | 20 | 0.5 |
D | 20 | 4 | 0.2 |
E | 10 | 10 | 1 |
F | 10 | 6 | 0.6 |
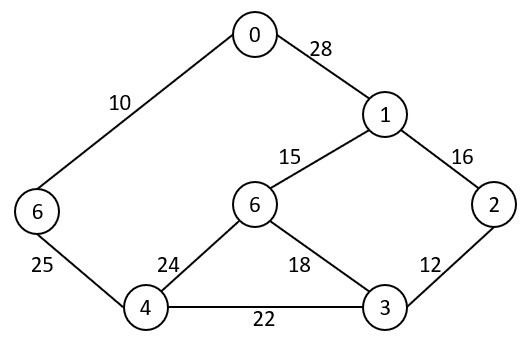
Q – Find the shortest path in the below graph from the source vertex 1 to all other vertices by using Dijkstra’s algorithm.
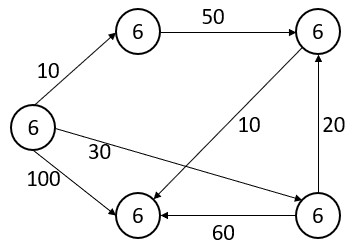
Q – When do Dijkstra and Bellman-ford algorithm both fail to find a shortest path? Can bellman ford detect all negative weight cycles in a graph? Apply bellman ford algorithm on the following graph:
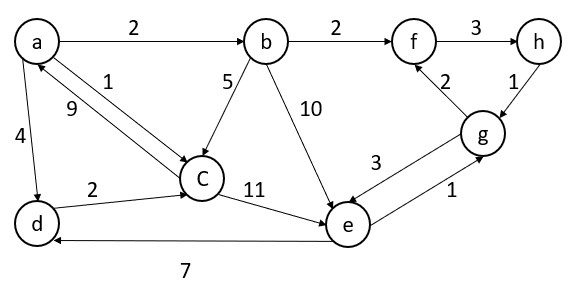
Design & Analysis of Algorithm
Assignment 6
Q – Define Greedy Approach.
Q – Define minimum spanning tree (MST). Write Prim’s algorithm to generate a MST for any given weighted graph. Generate MST for the following graph using Prim’s algorithm.
Q – Show how Prim’s algorithm can be implemented using heap. What would be the time complexity of an algorithm?
Q – Give the high-level description of kruskal’s algorithm to find the minimum cost spanning tree of an n-vertex undirected network.
Q – (i) State Bellman ford algorithm.
(ii) Consider following instance for simple knapsack problem. Find the solution using greedy method.
N = 8
P = {11, 21, 31, 33, 43, 53, 55, 65}
W = {1, 11, 21, 23, 33, 43, 45, 55}
M = 110
Design & Analysis of Algorithm
Assignment 7
Q – Describe and compare following algorithms to determine the minimum cost spanning tree:
(i) Kruskal’s algorithm
(ii) Prim’s algorithm
Q – Given a weighted directed graph G = (V, E) with source s and weight function W: E -> R, then write an algorithm to solve a single source path problem whose complexity is O(VE). Apply the same on the following graph.
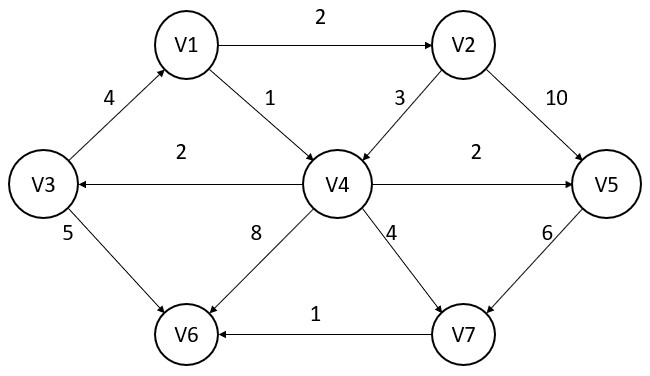
Q – What is Minimum Cost Spanning Tree? Explain kruskal’s algorithm and find MST of the graph. Also write its Time-Complexity?
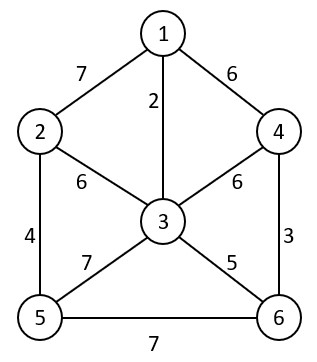
Q – Explain ‘greedy algorithm’. Write its pseudocode to prove that fractional knapsack problem has a greedy choice property.
Q – Consider the weights and values of items listed below. Note that there is only one unit of each item. The task is to pick a subset of these items such that their total weight is no more than 11kgs and their total value is maximized. Moreover, no item may be split. The total value of items picked by an optimal algorithm is denoted by Vopt. A greedy algorithm sorts the items by their value to weight ratios in descending order and packs them greedly, starting from the first item in the ordered list. The total value of items picked by the greedy algorithm is denoted by Vgreedy. Find the value of Vopt – Vgreedy.
Item | I1 | I2 | I3 | I4 |
W | 10 | 7 | 4 | 2 |
V | 60 | 28 | 20 | 24 |
Design & Analysis of Algorithm
Assignment 8
Q – Explain Single Source Shortest Path.
Q – Write down Dijkstra’s algorithm for it.
Q – Explain and write an algorithm for greedy method of algorithm design. Given 10 activities along with their start and finish time as
S = {A1, A2, A3, A4, A5, A6, A7, A8, A9, A10}
Start time = {1, 2, 3, 4, 7, 8, 9, 9, 11, 12}
Finish time = {3, 5, 4, 7, 10, 9, 11, 13, 12, 14}
Compute a schedule where the largest numbers of activities take place.
Q – What is Minimum Cost Spanning Tree? Explain kruskal’s algorithm and find MST of the graph. Also write its Time-Complexity?

Q – Define minimum spanning tree (MST). Write Prim’s algorithm to generate a MST for any given weighted graph. Generate MST for the following graph using Prim’s algorithm.