Unit 1
Father of Algorithm, What is Algorithm, Need of an algorithm, Algorithm Vs Program, Good Algorithm, Analysis of Algorithm, Comparison of running time, Asymptotic notation, Recurrence relation, Substitution method, Iterative method, Recurrence Tree Method, Master Theorem, Extended Master Theorem.
University Questions are from
(AKTU, IPU, DTU, MDU, LPU, VIT, SRM, Amity, PU, JMI and many more…)
Design & Analysis of Algorithm
Assignment 1
Q1 – Why do we study algorithm?
Q2 – Who is the Father of Algorithm?
Q3 – Who is the father of “Analysis of Algorithm”?
Q4 – List out the difference between Algorithm Vs Program?
Q5 – Describe the main characteristics of an algorithm defined by ‘Knuth’?
Design & Analysis of Algorithm
Assignment 2
Q1 – Define the following
(a) Big-Oh Notation (b) Big-omega Notation
(c) Theta Notation (d) Little oh Notation
(e) Little omega Notation
Q2 – Define different approaches of an algorithm?
Q3 – Define analysis of algorithm?
Q4 – What is a good algorithm?
Q5 – How would you calculate running time of an algorithm?
Design & Analysis of Algorithm
Assignment 3
Q1 – What is algorithm?
Q2 – “Tea making is also an algorithm”. Is this statement, right?
Q3 – Why is the algorithm finite?
Q4 – What is Space complexity?
Q5 – What is Time complexity?
Design & Analysis of Algorithm
Assignment 4
Q1 – What is the need of an algorithm?
Q2 – What do you see when you do a comparison between the two algorithms?
Q3 – Algorithm A1 has O(1) space complexity and have O(n) time complexity. Algorithm A2 has O(n^2) space complexity and O(log n) time complexity. Which one you will choose to solve the problem?
Q4 – Define recursion?
Q5 – Arrange the following growth rates in increasing order.
O(n^3), Ɵ(n^2), Ω(n^0.5), O(n^4), O(1), O(n), O(nlgn), O(n^2 lgn), Ω(n^2 lgn), Ɵ(n^1.5), Ɵ(nlgn).
Design & Analysis of Algorithm
Assignment 5
Q1 – Write about best case, average case & worst case of algorithm?
Q2 – What are randomized algorithms? Explain the term expected case.
Q3 – What is log*n?
Q4 – Can the master method be applied to the recurrence T(n) = 4T(n/3) + n2logn? Why or why not? Give an asymptotic upper bound for this recurrence.
Q5 – Find the time complexity using iterative search.
(a) T(n) = T(n-1) + √n
(b) T(n) = T(n-1) + log n
Design & Analysis of Algorithm
Assignment 6
Q1 – Compare the order of growth of log2n and √n.
Q2 – Compare the order of growth of 2n and n!
Q3 – Draw a table of Asymptotic Notation Properties?
Q4 – F(n+1) = F(n) + F(n-1). F(1) = 1, F(2) = 2 then what is F(6)?
Q5 – Find the time complexity of given code
For(i=0; i<n; i++)
For(j=1; j<n; j++)
printf(“Hello”);
Design & Analysis of Algorithm
Assignment 7
Q1 – Find the Big-Oh notation for the following function
(a) f(n) = 600
(b) f(n) = 5n2 + 124
(c) f(n) = 6n2 + 8n + 1234
(d) f(n) = 4n4 + 5n2 + 90
Q2 – Find the time complexity using recurrence function.
f(int n)
{
if(n <= 1)
return;
f(n/2);
f(n/2);
}
Q3 – Find the time complexity using recurrence tree method and iterative method.
(a) T(n) = 2T(n/2) + n
(b) T(n) = 5T(n/2) + n2
Q4 – Find the time complexity using master method.
(a) T(n) = 8T(n/2) + n2
(b) T(n) = 4T(n/2) + n2
Q5 – Find the time complexity using extended master method.
(a) T(n) = 5T(n/3) + n3logn
(b) T(n) = 7T(n/2) + n/logn
Design & Analysis of Algorithm
Assignment 8
Q1 – Solve the following recurrences by recurrence tree method:
- a) T (n) = 3T(n/2) + n
- b) T (n) = 2T(n/2) + n2
- c) T (n) = T(n/3) + T(2n/3) + n
Q2 – Solve the following recurrences by Master method:
- a) T (n) = 4T(n/2) + n
- b) T (n) = 4T(n/2) + n2
- c) T (n) = (n/2) + 1
Q3 – Solve the following recurrences by substitution method:
- a) T (n) = 2T(n/2) + n
- b) T (n) = T(n/2) + T(n/2) + 1
- c) T (n) = 2T(√n) + 1
Q4 – Solve the following recurrences by extended master method
(a) T(n) = T(n/2) + n0.5log2n
(b) T(n) = 3T(n/2) + logn/n
Q5 – Solve the following recurrences by iterative method
(a) T(n) = T(n/2) + log n
(b) T(n) = 2T(n/2) + 2n
Design & Analysis of Algorithm
Assignment 9
Find the time complexity
Q1 – T(n) = T(√n) + 1
Q2 – T(n) = T(√n) + lgn
Q3 – T(n) = 2T(√n) + lgn
Q4 – T(n) = 2T(√n) + 1
Q5 – T(n) = √nT(√n) + lgn
Design & Analysis of Algorithm
Assignment 10
Find the time complexity
Q1 – T(n) = √nT(√n) + √n
Q2 – T(n) = √nT(√n) + 1
Q3 – T(n) = T(log n) + 1
Q4 – T(n) = T(log n) + log n
Q5 – T(n) = T(log2n) + 1
Design & Analysis of Algorithm
Assignment 11
Q 1 – What do you mean by algorithm? Write the characteristics of algorithm.
Q 2 – What is recurrence relation? How is a recurrence solved using master’s theorem?
Q 3 – Prove if f(n) = am*nm + am-1*nm-1 + … + a1n + a0 and am > 0. Then
(a) f(n) = Ɵ(nm)
(b) f(n) = Ω(nm)
Q 4 – Write a short note on aggregate analysis.
Q 5 – Rank the following by growth rate:
N, 2lg√n, log n, log(log n), log2n, (lgn)lgn, 4, (3/2)n, n!
Design & Analysis of Algorithm
Assignment 12
Q – Explain how algorithms performance is analysed?
Q – Write the names of various design techniques of algorithm.
Q – Compare time complexity with space complexity.
Q – The recurrence T(n) = 7T(n/3) + n2 describes the running time of an algorithm A. Another competing algorithm B has a running time of S(n) = aS(n/9) + n2. What is the smallest value of ’a’ such that A is asymptotically faster than B.
Q – Why the statement “The running time of algorithm A is at least O(n2) is meaningless”? Explain.
Design & Analysis of Algorithm
Assignment 13
Q – Discuss the basic steps in the complete development of an algorithm.
Q – Write master method for solving recurrence relation of different types.
Q – Solve the following recurrence relations without using master method:
(i) Tn = 4Tn/2 + n3
(ii) Tn = Tn-1 + Tn-2
Q – Solve the following recurrence using Master Method:
T(n) = 4T(n/3) + n2
Q – Find the solution of the following recurrence relation in O-notation T(n) = 8T(n/2) + 3n2
Where n is an integer power of 2 and greater than 1.
Design & Analysis of Algorithm
Assignment 14
Q – How do you compare the performance of various algorithms?
Q – Order the following expressions by their asymptotic growth and justify your answer.
2n, n!, (log n)!, n3, 2log 2n, 22n, nloglogn, en
Q – Rank the following by growth rate:
N, 2lg√n, log n, log(log n), log2n, (lgn)lgn, 4, (3/2)n, n!
Q – What is asymptotic notation? Explain omega(Ω) notation?
Q – Determine the asymptotic order of the following functions: (2010 – 11) (5)
(i) f(n) = 3x2 + 5
(ii) f(n) = 2n + 5n + 3
(iii) f(n) = Σ i2 from i = 1 to n
(iv) f(n) = 5
(v) f(n) = n + 7
Design & Analysis of Algorithm
Assignment 15
Q – What is the smallest value of n such that an algorithm whose running time is 100n2 runs faster than an algorithm whose running time is 2n on the same machine?
Q – What is the importance of ‘average case analysis’ of algorithms?
Q – Why do we use asymptotic notation in the study of algorithm? Explain in brief various asymptotic notations and give their significance.
Q – Write an algorithm to find minimum and maximum elements simultaneously from a given list of elements. You are also required to discuss its running time.
Q – Consider the following function:
int RSUM(int A[ ], int n)
{
if (n) return RSUM(A, n-1) + A[n-1];
return 0;
}
Determine the asymptotic complexity of the function RSUM.
Design & Analysis of Algorithm
Assignment 16
Q – Solve the recurrence relation by iteration:
(i) T(n) = T(n-1) + n4
(ii) T(n) = T(n/4) + T(n/2) + n2
Q – Solve the recurrence relation for binary search algorithm using tree method.
Q – Two stacks are kept in a single array STK[Max] to utilize the array memory optimally:
STK[ ]:
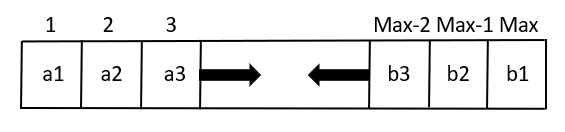
First stack grows in forward direction from start whereas second grows backwards from end.
Write Push 1, Push 2, Pop 1, Pop 2 for the two stacks.
Q – Consider a polynomial
P(x) = (………..(cn*x + cn-1)*x + cn-2)*x + cn-3*x …..)*x + c0.
Estimate the time complexity to evaluate the polynomial P(x).
Q – Show that following equalities are incorrect:
n2log n = Ɵ(n2)
Design & Analysis of Algorithm
Assignment 17
Q – What do you mean by algorithm? Write the characteristics of algorithm.
Q – What do you understand by asymptotic notations? Describe important types of asymptotic notations.
Q – Consider the recurrences
T(n) = 3T(n/3) + cn, and
T(n) = 5T(n/4) + n2 where c is constant and n is the number of inputs. Find the asymptotic bounds.
Q – Write recursive function to find nth Fibonacci number.
Q – Solve the recurrence T(n) = 2T(n/2) + n2 + 2n + 1
Design & Analysis of Algorithm
Assignment 18
Q – Solve the recurrence relation by iteration:
(i) T(n) = T(n-1) + n4
(ii) T(n) = T(n/4) + T(n/2) + n2
Q – Solve the recurrence relation using master method
T(n) = 3T(n1/3) + log 3n
Q – Find the time complexity of the recurrence relation
T(n) = n + T(n/10) + T(7n/5)
Q – Solve the following by recurrence tree method
T(n) = n + T(n/5) + T(4n/5)
Q – Solve the recurrence using recursion tree method: (2019-20) (7)
T(n) = T(n/2) + T(n/4) + T(n/8) + n
Design & Analysis of Algorithm
Assignment 19
Q – Let T(n) = aT(n/b) + c, then show that T(n) = O(log n), if a = 1, otherwise T(n) = O(n logba).
Q – Solve the recurrence relation using master method
T(n) = 3T(n1/3) + log 3n
Q Solve the following recurrences:
(i) T(n) = T(n/2) + T(n/4) + T(n/8) + n
(ii) T(n) = T(√n) + O(log n)
Q – The recurrence T(n) = 7T(n/2) + n2 describe the running time of an algorithm A. A competing algorithm A’ has a running time of T’(n) = aT’(n/4) + n2. What is the largest integer value for a so that A’ is asymptotically faster than A.
Q – Solve the recurrence T(n) = 4T(n/2) + n2.
Design & Analysis of Algorithm
Assignment 20
Q – What do you mean by algorithm? Write the characteristics of algorithm.
Q – Discuss the basic steps in the complete development of an algorithm.
Q – Solve the following recurrence using Master Method: T(n) = 4T(n/3) + n2
Q – What do you understand by asymptotic notations? Describe important types of asymptotic notations.
Q – What is the importance of ‘average case analysis’ of algorithms?

