Understanding the Activity Selection Problem
.
When you’re planning your day, have you ever wondered how to make the most of your time and attend as many events as possible without any clashes? That’s where the “Activity Selection Problem” comes into play.
In the world of algorithms, this problem is an interesting puzzle that can be applied to various scheduling scenarios.

If you can multi-tasking, then there is no problem but Activity Selection Algorithm can not multitask.
.
Introduction to Activity Selection
The Activity Selection Problem is a classic scheduling problem.
.
Problem – Given a list of activities, each with a ‘start time’ and an ‘finish time’, how can we select the maximum number of activities to attend without any overlap?
.
Imagine you’re planning to attend a conference with multiple talks and workshops. Each has a specific start and finish time. You want to figure out the best combination of sessions to attend without missing out on any interesting content.
If an experience person manually arranges the sessions, then he can do the optimal scheduling. But how to represent the logic of scheduling in computer? Following is a better logic which you implement in the algorithm.
.
How It Works
The key idea behind solving this problem is to select activities in such a way that they don’t clash with each other.
We will sort the ‘finish time’ of the activities, and write them into a table, and we will start from the first activity in that table. The goal is to attend as many activities as possible.
.
Algorithm of Activity Selection Algorithm
- Sort all the activities based on their ‘finish times’ in non-descending order. Use stable sort.
- Choose the first activity because it ends early.
- For the remaining activities, pick each one if its start time is greater than or equal to the finish time of the previously selected activity.
- Keep selecting activities that meet the condition until there are no more activities left to consider.
After that, when you’ve checked all the activities, you will have a list of selected activities that do not overlap with each other. This list represents the maximum number of activities you can attend without any conflicts.
.
Working of Activity Selection Problem
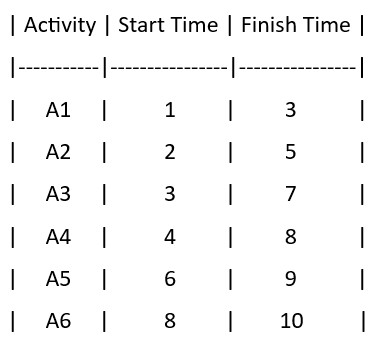
Given 10 activities along with their start and finish time as
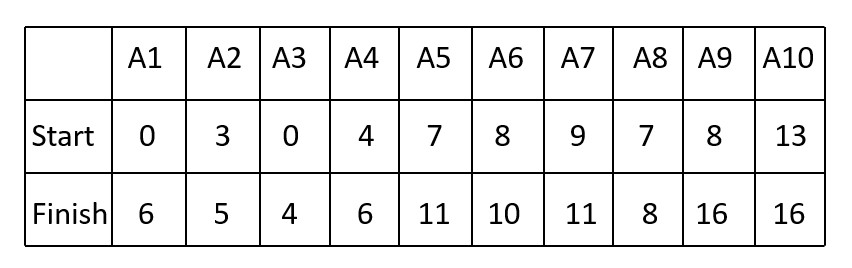
Now, we’ll sort the activities based on their finish times in non-descending order while keeping their relative order based on the original sequence (using a stable sort).
.
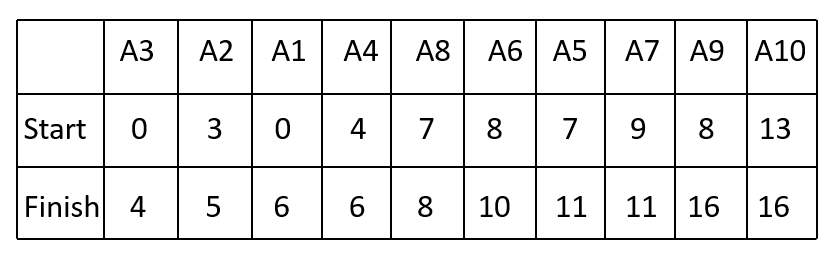
Sorted Finish Times
.
Now, let’s perform the greedy selection of activities
1. Start with Activity A3 (Start Time: 0, Finish Time: 4) since it has the earliest finish time.
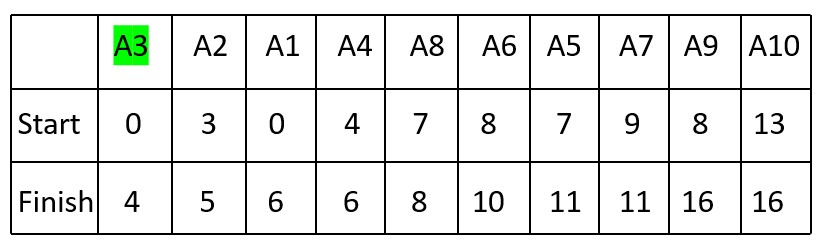
Selected Activity: A3
.
2. Activity A2 (Start Time: 3, Finish Time: 5) cannot be selected because it overlaps with A3.
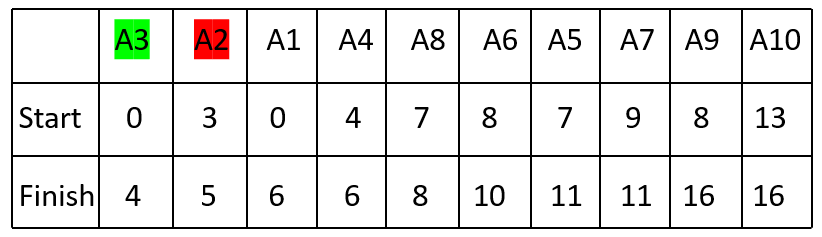
Selected Activity: A3
.
3. Activity A1 (Start Time: 0, Finish Time: 6) cannot be selected because it overlaps with A3.
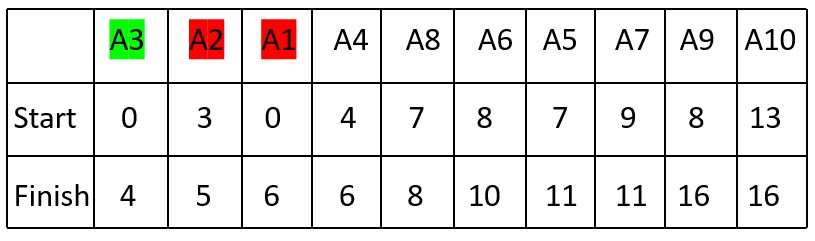
Selected Activity: A3
.
4. Activity A4 (Start Time: 4, Finish Time: 6) can be selected since it starts after A3 finishes.
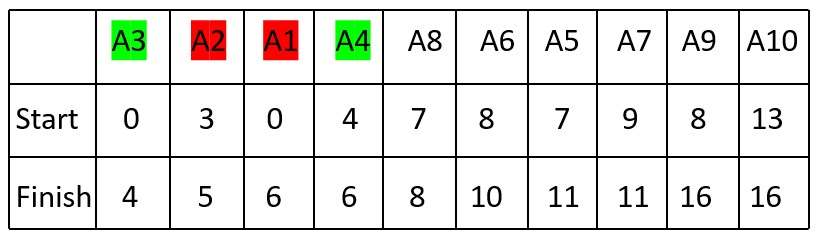
Selected Activities: A3, A4
.
5. Activity A8 (Start Time: 7, Finish Time: 8) can be selected as it starts after A4 finishes.
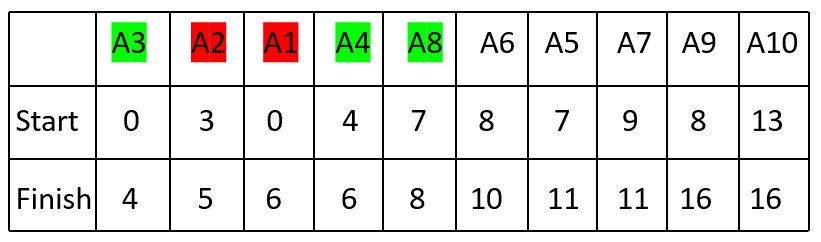
Selected Activities: A3, A4, A8
.
6. Activity A6 (Start Time: 8, Finish Time: 10) can be selected as it starts after A8 finishes.
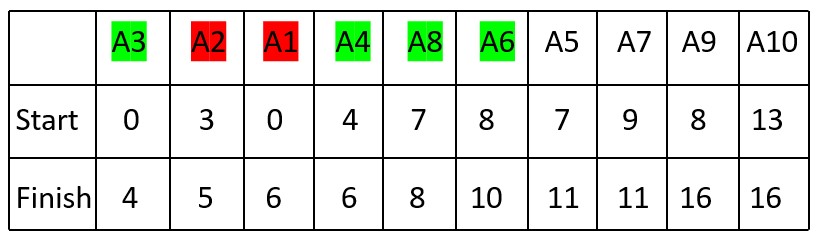
Selected Activities: A3, A4, A8, A6
.
7. Activity A5 (Finish Time: 11, Start Time: 7) cannot be selected because it overlaps with A6.
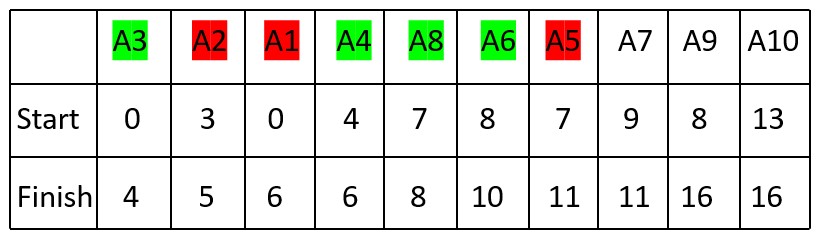
Selected Activity: A3, A4, A8, A6
.
8. Activity A7 (Finish Time: 11, Start Time: 9) cannot be selected because it overlaps with A6 (Start Time: 9).
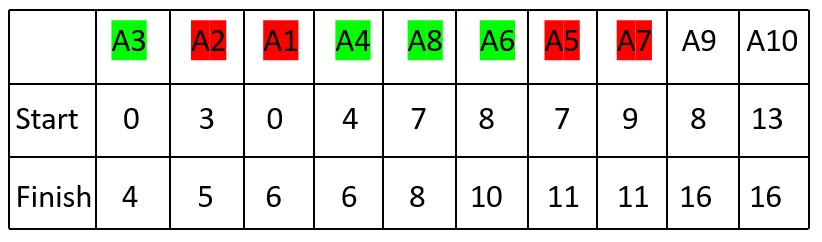
Selected Activities: A3, A4, A8, A6
.
9. Activity A9 (Finish Time: 16, Start Time: 8) cannot be selected because it overlaps with A6 (Start Time: 8).
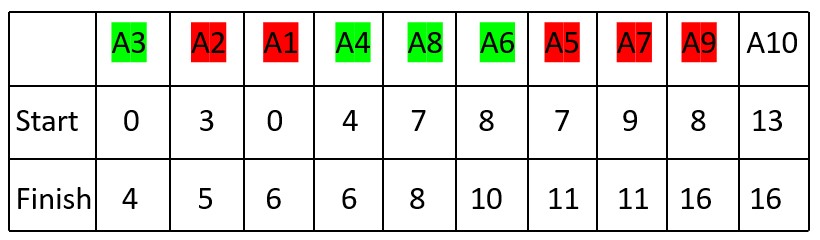
Selected Activities: A3, A4, A8, A6
.
10. Activity A10 (Finish Time: 16, Start Time: 13) can be selected as it starts after A6 finishes.
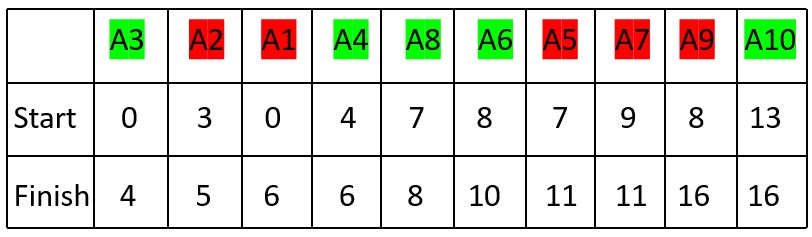
Selected Activities: A3, A4, A8, A6, A10
Selected Activities is A3, A4, A8, A6, A10 which is the output of Activity Selection Problem. Also, they do not overlap with each other. This is the optimal solution to the Activity Selection Problem for the given input.
.
Source Code for Activity Selection Problem
// COMPUTER GEEK – compgeek.co.in
// Write a program for Activity Selection Problem
#include <stdio.h>
int main()
{
int n;
// Prompt the user to enter the number of activities
printf(“Enter the number of activities: “);
scanf(“%d”, &n);
// Declare arrays for start and finish times
int start[n];
int finish[n];
// User will enter start and finish times for each activity
for (int i = 0; i < n; i++)
{
printf(“Enter start time for Activity %d: “, i + 1);
scanf(“%d”, &start[i]);
printf(“Enter finish time for Activity %d: “, i + 1);
scanf(“%d”, &finish[i]);
}
// Sort activities by finish time (you can use any sorting algorithm)
for (int i = 0; i < n – 1; i++)
{
for (int j = i + 1; j < n; j++)
{
if (finish[i] > finish[j])
{
// Swap finish times
int temp = finish[i];
finish[i] = finish[j];
finish[j] = temp;
// Swap start times to maintain the relative order
temp = start[i];
start[i] = start[j];
start[j] = temp;
}
}
}
// Select and print the activities
printf(“Selected Activities: \n”);
// The first activity is always selected
int i = 0;
printf(“Activity %d: Start time = %d, Finish time = %d\n”, i + 1, start[i], finish[i]);
// Consider the rest of the activities
for (int j = 1; j < n; j++)
{
// If this activity has a start time greater than or equal to
// the finish time of the previous activity, select it
if (start[j] >= finish[i])
{
printf(“Activity %d: Start time = %d, Finish time = %d\n”, j + 1, start[j], finish[j]);
i = j; // Update the index of the last selected activity
}
}
return 0;
}
// COMPUTER GEEK – compgeek.co.in
// Write a program for Activity Selection Problem
#include <iostream>
using namespace std;
int main()
{
int n;
// User will enter the number of activities
cout << “Enter the number of activities: “;
cin >> n;
// Declare arrays for start and finish times
int start[n];
int finish[n];
// User will enter start and finish times for each activity
for (int i = 0; i < n; i++)
{
cout << “Enter start time for Activity ” << i + 1 << “: “;
cin >> start[i];
cout << “Enter finish time for Activity ” << i + 1 << “: “;
cin >> finish[i];
}
// Sort activities by finish time (you can use any sorting algorithm)
for (int i = 0; i < n – 1; i++)
{
for (int j = i + 1; j < n; j++)
{
if (finish[i] > finish[j])
{
// Swap finish times
int temp = finish[i];
finish[i] = finish[j];
finish[j] = temp;
// Swap start times to maintain the relative order
temp = start[i];
start[i] = start[j];
start[j] = temp;
}
}
}
// Select and print the activities
cout << “Selected Activities: \n”;
// The first activity is always selected
int i = 0;
cout << “Activity ” << i + 1 << “: Start time = ” << start[i] << “, Finish time = ” << finish[i] << endl;
// Consider the rest of the activities
for (int j = 1; j < n; j++)
{
// If this activity has a start time greater than or equal to the finish time of the previous activity, select it
if (start[j] >= finish[i])
{
cout << “Activity ” << j + 1 << “: Start time = ” << start[j] << “, Finish time = ” << finish[j] << endl;
i = j; // Update the index of the last selected activity
}
}
return 0;
}
// COMPUTER GEEK – compgeek.co.in
// Write a program for Activity Selection Problem
import java.util.Scanner;
public class ActivitySelection
{
public static void main(String[] args)
{
Scanner scanner = new Scanner(System.in);
// User will enter the number of activities
System.out.print(“Enter the number of activities: “);
int n = scanner.nextInt();
// Declare arrays for start and finish times
int[] start = new int[n];
int[] finish = new int[n];
// Prompt the user to enter start and finish times for each activity
for (int i = 0; i < n; i++)
{
System.out.print(“Enter start time for Activity ” + (i + 1) + “: “);
start[i] = scanner.nextInt();
System.out.print(“Enter finish time for Activity ” + (i + 1) + “: “);
finish[i] = scanner.nextInt();
}
// Sort activities by finish time (you can use any sorting algorithm)
for (int i = 0; i < n – 1; i++)
{
for (int j = i + 1; j < n; j++)
{
if (finish[i] > finish[j])
{
// Swap finish times
int tempFinish = finish[i];
finish[i] = finish[j];
finish[j] = tempFinish;
// Swap start times to maintain the relative order
int tempStart = start[i];
start[i] = start[j];
start[j] = tempStart;
}
}
}
System.out.println(“Selected Activities: “);
// The first activity is always selected
int i = 0;
System.out.println(“Activity ” + (i + 1) + “: Start time = ” + start[i] + “, Finish time = ” + finish[i]);
// Consider the rest of the activities
for (int j = 1; j < n; j++)
{
// If this activity has a start time greater than or equal to
// the finish time of the previous activity, select it
if (start[j] >= finish[i]) {
System.out.println(“Activity ” + (j + 1) + “: Start time = ” + start[j] + “, Finish time = ” + finish[j]);
i = j; // Update the index of the last selected activity
}
}
}
}
# COMPUTER GEEK – compgeek.co.in
# Write a program for Activity Selection Problem
def activity_selection(n, start, finish):
selected_activities = []
# Sort activities by finish time
activities = list(zip(start, finish))
activities.sort(key=lambda x: x[1])
# The first activity is always selected
selected_activities.append(activities[0])
i = 0
# Consider the rest of the activities
for j in range(1, n):
# If this activity has a start time greater than or equal to
# the finish time of the previous activity, select it
if activities[j][0] >= selected_activities[i][1]:
selected_activities.append(activities[j])
i = i + 1
return selected_activities
if __name__ == “__main__”:
# Prompt the user to enter the number of activities
n = int(input(“Enter the number of activities: “))
start = []
finish = []
# User will enter start and finish times for each activity
for i in range(n):
start_time = int(input(f”Enter start time for Activity {i + 1}: “))
finish_time = int(input(f”Enter finish time for Activity {i + 1}: “))
start.append(start_time)
finish.append(finish_time)
result = activity_selection(n, start, finish)
print(“Selected Activities:”)
for i, (start_time, finish_time) in enumerate(result):
print(f”Activity {i + 1}: Start time = {start_time}, Finish time = {finish_time}”)
Time and Space Complexity of Activity Selection Problem
- The sorting step takes O(n log n), and the selection step takes O(n). So, the total time complexity is O(n log n).
- The space complexity is O(1), which means it uses a constant amount of memory.
.
Advantages of Activity Selection Problem
- Simple and efficient algorithm.
- Finds a solution that maximizes the number of activities.
- Greedy algorithms provide a globally optimal solution when selecting a maximum number of non-overlapping activities.
- Easy to Extend.
- Fast Execution.
- Minimal Resource Utilization.
.
Disadvantages of Activity Selection Problem
- The greedy algorithm does not account for dependencies among activities. In some scheduling problems, activities must be performed in a specific order or in parallel with others.
.
Applications of Activity Selection Problem
- Task scheduling in operating systems.
- Scheduling classes in schools and universities.
- Job scheduling in factories.
- Optimizing resource usage in various industries.
So, the next time you’re faced with a scheduling challenge, remember the Activity Selection Problem and how it can help you make the most of your time!
Test Yourself
Q1- Describe the key idea behind solving the Activity Selection Problem.
The key idea is to select maximum activities based on their finish times in non-decreasing order. Starting with the activity that finishes earliest, choose activities that don’t overlap with the previously selected ones.
Q2- Why is the sorting of activities based on finish times necessary in the Activity Selection algorithm?
Sorting by finish times ensures that the selected activities end as early as possible, maximizing the number of activities that can be scheduled without overlap.
Q3- Can the Activity Selection Problem handle scenarios where activities have dependencies or specific order requirements?
No, the greedy approach doesn’t account for dependencies or order requirements; it’s suitable for non-overlapping activities only.
Q4- What is the significance of a stable sort when sorting activities by finish times?
A stable sort preserves the relative order of activities with the same finish times, ensuring the original sequence is maintained.
Q5- What is the goal of the Activity Selection Problem?
Minimize the number of activities
Maximize the number of non-overlapping activities
Equalize the start and finish times
Randomly select activities
Ans – (2)
Explanation – The goal is to maximize the number of non-overlapping activities
Q6- Why is it important to sort activities by finish times?
It’s not necessary
To minimize the number of activities
To maximize the number of activities
To minimize time complexity
Ans – (3)
Explanation – Sorting by finish times maximizes the number of activities
Q7- Which data structure is typically used to implement the Activity Selection Problem?
Stack
Queue
Linked list
Array
Ans – (4)
Explanation – Arrays are commonly used to represent activities in this problem.
Q8- In the Activity Selection algorithm, which activity is selected first?
The activity with the earliest finish time
The activity with the latest finish time
The activity with the lowest priority
The activity with the highest weight
Ans – (1)
Explanation –
The activity with the earliest finish time is selected first, so the correct answer is (1).
Q9- You have a set of 6 activities with the following start and finish times:
Using the greedy approach, calculate the maximum number of activities that can be selected.
The maximum number of activities that can be selected using the greedy approach is 3 (A1, A3, A6).
Q10- You have a set of 5 activities with the following start and finish times
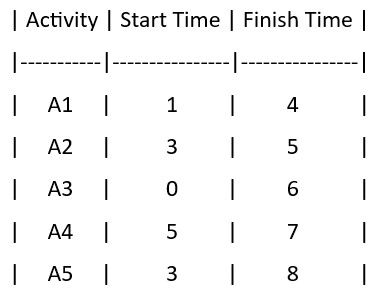
Calculate the maximum number of activities that can be selected using the greedy approach.
The maximum number of activities that can be selected using the greedy approach is 2 (A1, A4).
Q11- You have a set of 7 activities with the following start and finish times
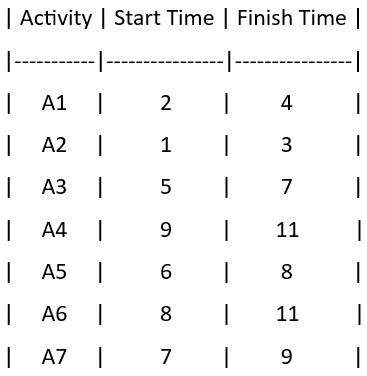
Calculate the maximum number of activities that can be selected using the greedy approach.
Sort the finish time
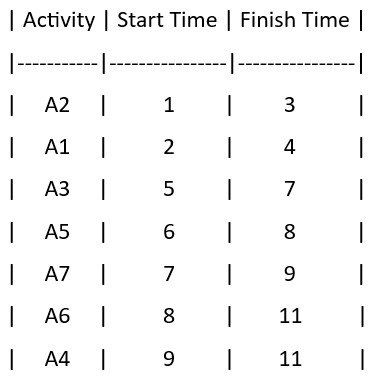
The maximum number of activities that can be selected using the greedy approach is 4 (A2, A3, A7, A4).