Design & Analysis of Algorithm logo

DAA Unit 1 Part 3 MCQs

PREV
NEXT
Menu
Unit 1

Father of Algorithm, What is Algorithm, Need of an algorithm, Algorithm Vs Program, Good Algorithm, Analysis of Algorithm, Comparison of running time, Asymptotic notation, Recurrence relation, Subtitution method, Iterative method, Recurrence Tree Method, Master Theorem, Extended Master Theorem.

Q41 – Find the time complexity
T(n) = T(n-1) + 1
T(1) = 1
  1. O(logn)
  2. O(n)
  3. O(nlogn)
  4. O(n2)

Ans – (2)

Explanation – 

T(n) = T(n-1) +1

Q42 – Find the time complexity
T(n) = T(n-1) + n
T(1) = 1
  1. O(logn)
  2. O(n)
  3. O(nlogn)
  4. O(n2)

Ans – (2)

Explanation –

T(n) = T(n-1) + n T(1) = 1

Q43 – Find the time complexity
T(n) = T(n-1) + n2
T(1) = 1
  1. O(n2logn)
  2. O(nlogn)
  3. O(n3)
  4. O(n2)

Ans – (3)

Explanation – T(n) = T(n-1) + n^2 T(1) = 1

Q44 – Find the time complexity
T(n) = T(n-1) + logn
T(1) = 1
  1. O(logn)
  2. O(n)
  3. O(nlogn)
  4. O(n2)

Ans – (3)

Explanation –

T(n) = T(n-1) + logn T(1) = 1

Q45 – Find the time complexity
T(n) = T(n-1) + 1/n
T(1) = 1
  1. O(logn)
  2. O(n)
  3. O(nlogn)
  4. O(n2)

Ans – (1)

Explanation –

T(n) = T(n-1) + 1/n T(1) = 1

Q46 – Find the time complexity
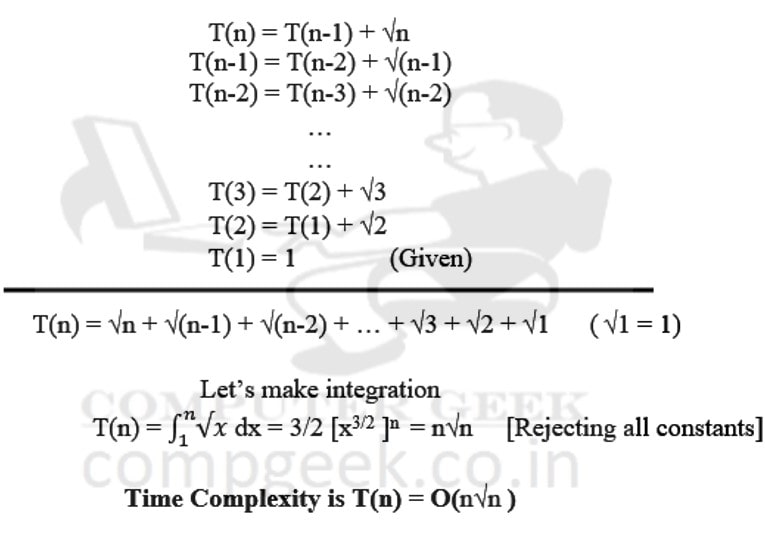
T(n) = T(n-1) + √n
T(1) = 1
  1. O(√n)
  2. O(n)
  3. O(n√n)
  4. O(n2)

Ans – (3)

Explanation –

T(n) = T(n-1) + √n T(1) = 1

Q47 – Find the time complexity
T(n) = 2T(n-1) + n
T(1) = 1
  1. O(nlogn)
  2. O(n2)
  3. O(2n)
  4. O(4n)

Ans – (3)

Explanation –

T(n) = 2T(n-1) + n T(1) = 1

Q48 – Find the time complexity
T(n) = T(n-1) + 2n
T(1) = 1
  1. O(nlogn)
  2. O(n2)
  3. O(2n)
  4. O(4n)

Ans – (3)

Explanation –

T(n) = T(n-1) + 2^n T(1) = 1

Q49 – Find the time complexity
T(n) = 2T(n-1) + 2n
T(1) = 1
  1. O(2n*n)
  2. O(2n*√n)
  3. O(2n/n)
  4. O(4n)

Ans – (1)

Explanation –

T(n) = 2T(n-1) + 2n T(1) = 1

Q50 – Find the time complexity
T(n) = 2T(n-1) + logn
T(1) = 1
  1. O(2n*n)
  2. O(2n*√n)
  3. O(2n)
  4. O(4n)

Ans – (3)

Explanation – 

T(n) = 2T(n-1) + logn

Q51 – Find the time complexity
T(n) = √5T(n-1) + n
T(1) = 1
  1. O(√5n)
  2. O(√5n)
  3. O(√5n/n)
  4. O(5n)

Ans – (2)

Explanation – T(n) = √5T(n-1) + n

Q52 – Find the time complexity
T(n) = T(n/2) + n
T(1) = 1
  1. O(logn)
  2. O(n)
  3. O(nlogn)
  4. O(n2)

Ans – (2)

Explanation – T(n) = T(n/2) + n

Q53 – Find the time complexity
T(n) = 2T(n/2) + 1
T(1) = 1
  1. O(logn)
  2. O(n)
  3. O(nlogn)
  4. O(n2)

Ans – (2)

Explanation – T(n) = 2T(n/2) + 1

Q54 – Find the time complexity
T(n) = 2T(n/2) + n
T(1) = 1
  1. O(logn)
  2. O(n)
  3. O(nlogn)
  4. O(n2)

Ans – (3)

Explanation – 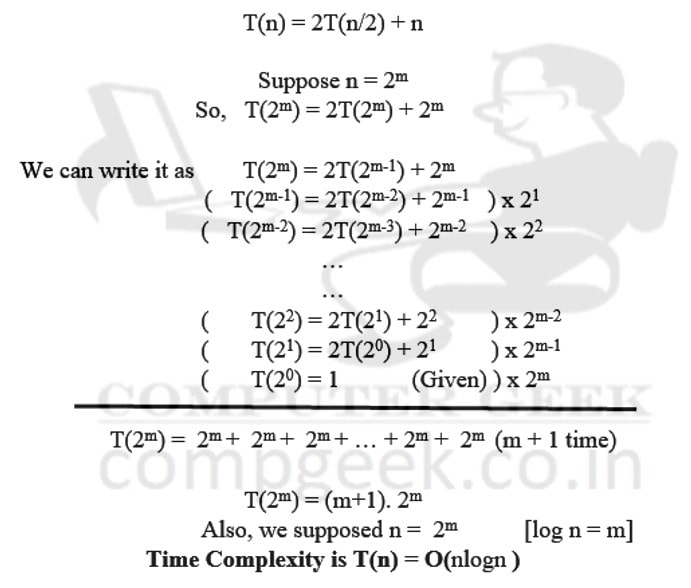T(n) = 2T(n/2) + n

Q55 – Find the time complexity
T(n) = 4T(n/2) + n2
T(1) = 1
  1. O(logn)
  2. O(n)
  3. O(nlogn)
  4. O(n2logn)

Ans – (4)

Explanation –

T(n) = 4T(n/2) + n^2

Q56 – Find the time complexity
T(n) = 3T(n/2) + n
T(1) = 1
  1. O(3n/2)
  2. O(n1.59)
  3. O(n2)
  4. O(n3)

Ans – (2)

Explanation –

T(n) = 3T(n/2) + n

Q57 – Find the time complexity
T(n) = 2T(n/3) + n
T(1) = 1
  1. O(logn)
  2. O(n)
  3. O(nlogn)
  4. O(n2)

Ans – (2)

Explanation –

T(n) = 2T(n/3) + n

Q58 – Find the time complexity
T(n) = 7T(n/2) + n2
T(1) = 1
  1. O(logn)
  2. O(n7/2)
  3. O(nlog27 )
  4. O(n3

Ans – (3)

Explanation –

T(n) = 7T(n/2) + n^2

Q59 – Find the time complexity
T(n) = 5/2T(3n/2) + n
T(1) = 1
  1. O(log1.52.5)
  2. O(n^log1.52.5)
  3. O(nlogn)
  4. O(n5/2)

Ans – (2)

Explanation – 

T(n) = 5/2T(3n/2) + n

Q60 – Find the time complexity
T(n) = 2T(n/4) + √n
T(1) = 1
  1. O(√nlogn)
  2. O(√n)
  3. O(n√n)
  4. O(n2)

Ans – (1)

Explanation –

T(n) = 2T(n/4) + √n

PREV
NEXT

BOOKS

Algorithm T H CoremanAlgorithm by Udit AgarwalAlgorithm Ellis HorowitzData Structure & Algorithm Made Easy Narasimha

 

GATE Study Material
Previous Year Paper
Subjective Questions