Unit 4
Divide & Conquer:- Matrix Multiplication, Strassen’s Multiplication, Convex Hull, Searching.
University Questions are from
(AKTU, IPU, DTU, MDU, LPU, VIT, SRM, Amity, PU, JMI and many more…)
Design & Analysis of Algorithm
Assignment 1
Q – Write an efficient algorithm for finding Kth smallest element in an array of size n.
Q – Write divide and conquer approach for binary search and find its average case complexity.
Q – Define Convex hull?
Q – What is matrix chain multiplication problem? Describe a solution for matrix chain multiplication problem.
Q – Describe in detail the Strassen’s Matrix Multiplication algorithms based on divide and conquer strategies with suitable example.
Design & Analysis of Algorithm
Assignment 2
Q – Explain searching technique using divide and conquer approach.
Q – List out the disadvantages of divide and conquer algorithm.
Q – What is advantage over binary search over linear search? Also state limitations of binary search.
Q – Show all the steps of Strassen’s matrix multiplication algorithm to multiply the following matrices (2015-16) (10)
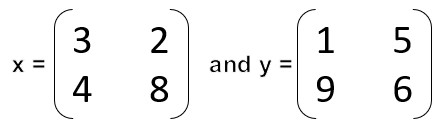
Q – Construct binary expression tree from the following traversals: (2008-09) (5)
Inorder: 4+3+2*1
Preorder: +4*+3 2 1
Design & Analysis of Algorithm
Assignment 3
Q – What is advantage over binary search over linear search? Also state limitations of binary search.
Q – Write a randomized algorithm for two dimensional convex-hull problem. Find the time complexity of the algorithm.
Q – Give an algorithm to count the number of leaf nodes in a binary tree t. What is its computing time?
Q – Given an integer x and a positive number n, use divide & conquer approach to write a function that computes xn with time complexity O(log n).
Q – Describe in detail the Strassen’s Matrix Multiplication algorithms based on divide and conquer strategies with suitable example.

