Q1- What do you mean by algorithm? Write the characteristics of algorithm? (AKTU 2013-14, IPU) (Marks 05)
Definition of an algorithm is “A step by step procedure for solving a specific type of problem. The problem can be solved manually or more usually on a machine”.
The Computing definition of algorithm is “an algorithm is a finite sequence of instructions that specify a sequence of operations to be carried out to solve a specific problem or class of problems”.
Characteristics are –
- Input – There can be zero or more inputs such that there is no input in the program of hello world.
- Output – At least one output must come.
- Definiteness – Every instruction should be very clear and unambiguous. There should be no doubt or misunderstanding in the instruction.
- Effectiveness – Every instruction should be very basic and possible and result-giving.
- Finiteness – The algorithmic instruction must end after a finite number. That is why, we definitely write the ‘End’ after the algorithm is over.
Q2- What do you mean by analysis or complexity of an algorithm? Give its types and cases. (IPU) (Marks 05)
An algorithm can be analysed in two ways. One is the time it takes and the second is the space it takes.
Types of Complexities
(i) Time Complexity: – In computer science, the time complexity is the number of operations done by the operating system from the start of the algorithm to the end of the algorithm.
(ii) Space complexity: – The amount of space or the number of bits required to solve a problem is referred to as its space complexity.
Our problem is not the space taken by that algorithm. In today’s world, space is unlimited. Our problem is the time. Time is valuable. So, cases only belong to the time complexity.
The number of cases is
(i) Worst Case Time Complexity-
It is the maximum time taken by an algorithm to solve a problem.
(ii) Best Case Time Complexity-
It is the minimum time taken by an algorithm to solve a problem.
(iii) Average Case Time Complexity-
It is in between the best case and worst case.
This means the average time is taken by an algorithm to solve a problem.
In the randomized algorithm, we have only one case
(i) Expected Case –
The expected time is the amount of time it takes your method to compute the probability distribution of expected input sets.
Q3- What do you understand by asymptotic notations? Describe important types of asymptotic notations. (AKTU 2013-14) (Marks 05)
OR
Discuss asymptotic notations. (IPU) (Marks 10)
To represent complexity, there is an approximation method, which is also known as Asymptotic Notations. It is like an error method to approximate function means if you get an answer “5n + 2n^2 + nlogn”, then you have to focus on what’s important by abstracting away lower-order terms (like 5n, nlogn) and constant factors (like 2).
The amount of time, storage required to execute an algorithm, determine its efficiency. Asymptotic notations are used to calculate efficiency. An algorithm’s performance may differ depending on the type of input. The performance will change as the input size increases.
Asymptotic Notation | Symbol | Nature | ||
1 | Big Oh | O | O ≈ ≤ | Upper Bound – Worst Case |
2 | Big Omega | Ω | Ω ≈ ≥ | Lower Bound – Best Case |
3 | Theta | Θ | Θ ≈ = | Average Bound – Average Case (Exact Time) |
4 | Small oh | o | o ≈ < | |
5 | Small omega | ω | ω ≈ > |
- Big-Oh (O) = {f(n): there exist positive constants c and n0, such that 0 ≤ f(n) ≤ g(n) for all n ≥ n0}
This algorithm execution will take at least f(n) time and at most, g(n) time, no matter how much easy problem is there. So, g(n) time is one of the worst conditions in which the algorithm will give results. g(n) time will be equal to the f(n) time or more than f(n) time but not less than f(n) time.
- Big-Omega (Ω) = {f(n): there exist positive constants C and no, such that 0 ≤ C.g(n) ≤ f(n) for all n ≥no}
g(n) is an asymptotic lower bound for f(n) for larger n (n ≥ no)
Assume you calculated an algorithm’s time complexity n2, but you already know from prior experience that the time complexity of this algorithm is less than n2. You must, however, respond in the form of n, and because nlogn is very little, you have to write n2, followed by the symbol Ω, which represents the best-case situation.
- Theta (Θ) = {f(n): there exist positive constants C1, C2 and no, such that 0 ≤ C1.g(n) ≤ f(n) ≤ C2.g(n) for all n ≥no}
g(n) is asymptotically tightly bound for f(n) for larger n (n ≥ no)
It means Θ = O ∩ Ω
- Small-Oh (o) ={f(n): there exist positive constants C and no, such that 0 ≤ f(n) < C.g(n) for all n ≥no}
The only difference between Big-Oh and Small-oh is that Big-Oh has f(n) ≤ C.g(n) and small-oh has f(n) < C.g(n).
- Small-Omega (ω) ={f(n): there exist positive constants C and no, such that 0 ≤ C.g(n) < f(n) for all n ≥no}
The only difference between Big-Omega and Small-omega is that Big-Omega has C.g(n) ≤ f(n) and small-oh has C.g(n) < f(n).
Q4- If f(n) = 100*2n + n5 + n, then show that f(n) = O(2n).
There is a statement in the algorithm that n is a very big number. So, all the lower order term like (n5 + n) are vanished when a higher order like 2n is there.
Also, big-Oh always dropped all the constants. We are calculating the time complexity of function f(n), so we only put a pressure on the growth of function. A linear function always grows linearly, a logarithmic function always grows logarithmically, a quadratic function always grows quadratically. So, no matter if a constant is there or not, f(n) will always remain O(2n).
Q5- Write Master’s theorem and explain with suitable examples.
It is a simplistic way to find time complexity. Master’s method works only for the recurrence T(n) = aT(n/b) + c1*nk, where a ≥ 1, b ≥ 1, c1 and k are constant.
(A) if n^(logba) > c1*nk , then answer is n^(logba).
(B) if n^(logba) < c1*nk , then answer is c1*nk
(C) if n^(logba) = c1*nk , then answer is n^(logba)*logn.
Example-
- Find the time complexity of T(n) = T(n/2) + n.
Apply master’s theorem.
In this equation, a = 1, b = 2, c1 = 1 and k = 1
-> n^(logba) = n^(log21) = n0 = 1
-> c1*nk is n
-> Case B occurs
-> (B) if n^(logba) < c1*nk , then answer is c1*nk
-> O(n) is the answer.
- Find the time complexity of T(n) = 2T(n/2) + 1.
Apply master’s theorem.
In this equation, a = 2, b = 2, c1 = 1 and k = 0
-> n^(logba) = n^(log22) = n1 = n
-> c1*nk is 1
-> Case A occurs
-> (A) if n^(logba) > c1*nk , then answer is n^(logba).
-> O(n) is the answer.
- Find the time complexity of T(n) = 2T(n/2) + n.
Ans –
Apply master’s theorem.
In this equation, a = 2, b = 2, c1 = 1 and k = 1
-> n^(logba) = n^(log22) = n1 = n
-> c1*nk is n
-> Case C occurs
-> (C) if n^(logba) = c1*nk , then answer is n^(logba)*logn.
-> O(n*logn) is the answer.
Q6- The recurrence T(n) = 7T(n/2) + n2 describe the running time of an algorithm A. A competing algorithm, let say A’ has a running time T’(n) = @T’(n/4) + n2. What is the largest integer value of @, for which A’ is asymptotically faster than A? (AKTU 2017-18) (Marks 10).
Algorithm A equation
=> T(n) = 7T(n/2) + n2 (equation 1)
To know the running time of Algorithm A, we apply master’s method.
=> a = 7, b = 2, f(n) = n2
=> n^(logba) = n^(log27) = n^2.81
=> f(n) = n2
=> In the master’s method, case A occurs
=> (A) if n^(logba) > c1*nk , then answer is n^(logba).
=> O(n2.81)
Algorithm B equation
=> T(n) = @T(n/4) + n2 (equation 2)
To know the running time of Algorithm A, we apply master’s method.
=> a = @, b = 4, f(n) = n2
=> n^(logb@) = n^(log4@) < n^2.81
=> f(n) = n2
=> In the master’s method, same case occurs
So, we have to find the @ value so that n^(log4@) < n^2.81
Taking log both sides
=> log(n^(log4@)) < log(n^2.81)
=> log4@*logn < 2.81*logn
=> log4@ < 2.81
=> @ < 4*2.81
=> @ < 49.18
If in the computing we have (int @), then we can say that @ < 49. So, @ = 48, for which A’ is asymptotically faster than A.
Q7- Solve the following recurrence T(n) = T(√n) + O(logn) (AKTU 2014-15) (Marks 10)
=> T(n) = T(√n) + O(logn)
Let n = 2m, So n1/2 = 2m/2
=> T(2m) = T(2m/2 ) + log (2m )
Iterative method starts
=> T(2m) = T(2m/2 ) + m (equation 1)
=> T(2m/2) = T(2m/4) + m/2
=> T(2m/4) = T(2m/8) + m/4
=> …
=> …
=> T(22) = T(21) + 2
=> T(21) = T(20) + 1
=> T(20) = 1 (T(20) = T(1) = 1)
Adding all the equations, we get
=> T(2m) = m + m/2 + m/4 + … + 4 + 2 + 1 +1
=> This is a G.P. Series and sum is a(1-rn)/(1-r) where a =first term, r = ratio and n = no of terms
=> T(2m) = m(1 – (½)m/2)/(1-1/2)
=> T(2m) = m [Removing all the constant terms]
=> Also, n = 2m , So m = logn
=> T(2m) = O(logn)
Q8- What do you mean by recursion? Explain your answer with an example.
Recursion – It means to repeat itself.
Recursion is only applicable to functions or processes that repeat themselves. That is, a recursive function is one that calls itself from its body, either conditionally or unconditionally. Example – T(n) = T(n-1) + 1
Let T(n) is a mathematical function to approximate recursive function.
Rules –
- If the given instance of the problem is small or simple enough, just solve it.
- Otherwise, reduce the problem to one or more, simpler instances of the same problem.
Example – Fibonacci series
1 1 2 3 5 8 13 21 34 55 . . .
In this, sequence is made by the addition of the last two terms
1 + 1 = 2, 1 + 2 = 3, 2 + 3 = 5, ….
Recurrence function -> f(n + 1) = f(n) + f(n – 1)
Q9- What is recursion tree? Describe.
In the recursion tree method, we make a tree with the help of the recurrence equation.
If equation is T(n) = a T(n/b) + C, then we make a recurrence tree.
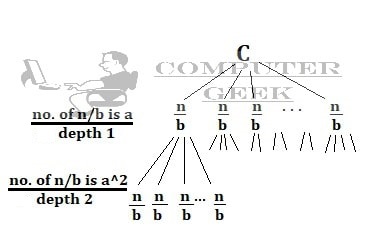
Example – Draw the recursion tree T(n) = 2T(n/2) + n
Compiling Time = 2T(n/2) Running Time = n
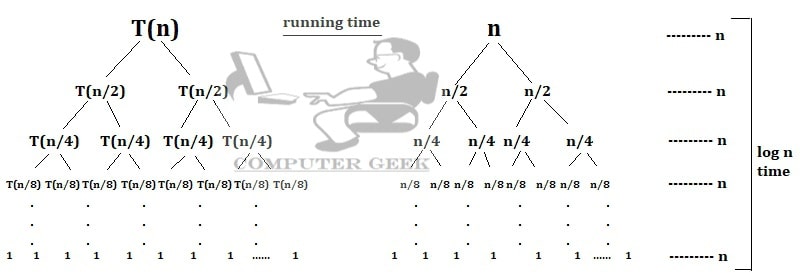
After summation of all the operations
= n + n + n + … + n [log n time]
= n.logn
= O(n.logn) is the Ans
Q10- Solve the recurrence T(n) = T(n-1) + T(n-2) + 1, when T(0) = 0 and T(1) = 1
By recurrence tree method, we get
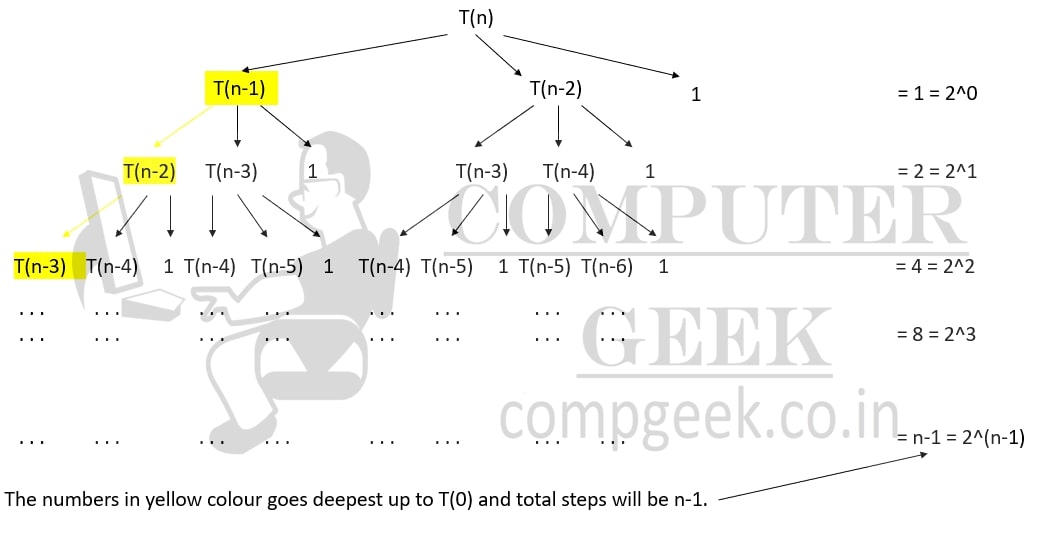
The running time we get when T(n) is broken is 20. When further broken down we get 21, 22, 23, …, 2n-1.
Sum = 20 + 21 + 22 + 23 + …+ 2n-1
This is a G.P. Series and sum = a(rn – 1)/(r-1) where r = 2
=> 20(2n-1 – 1)/(2-1)
=> 2n
The time complexity of the recurrence T(n) = T(n-1) + T(n-2) + 1 is O(2n).

