Recurrence Relation

Definition:- ये Relation अपने आप को ही call करता है।

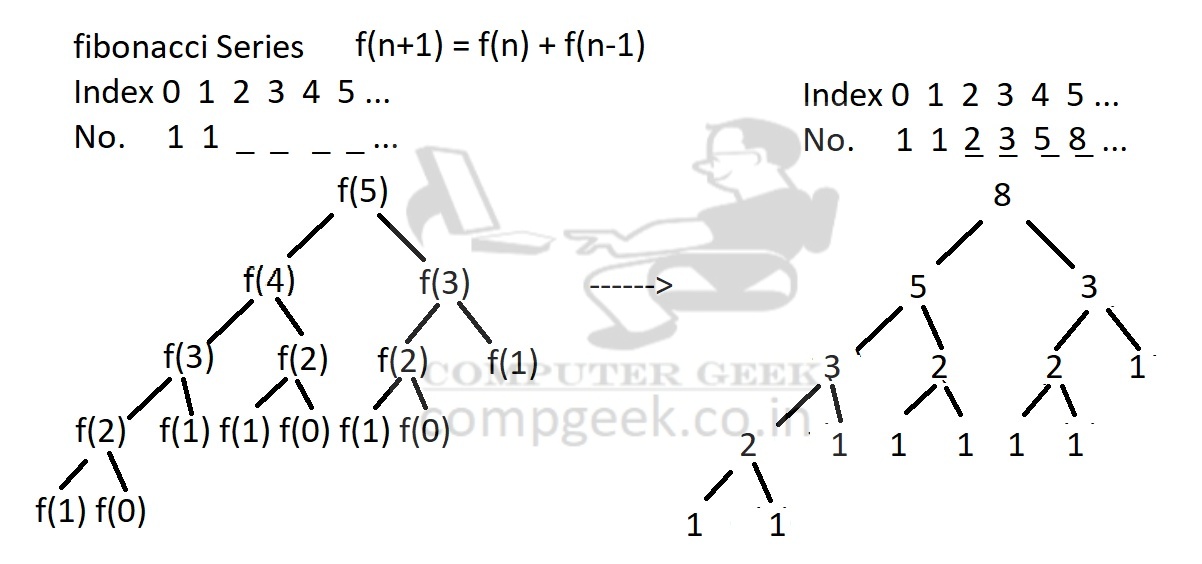
Fibonacci Series इसका एक Example है –

1   1   2   3   5   8   13   21    34    55 . . .

इस series का कोई अंत नहीं है। इस series में कोई भी number उससे पहले वाले 2 numbers का जोड़ होता है।

1 + 1 = 2, 1 + 2 = 3, 2 + 3 = 5, ….

इसका Recurrence function f(n + 1) = f(n) + f(n – 1) होगा । मतलब (n + 1)th number, nth number और (n-1)th number का जोड़ होगा ।

Recurrence – यह एक mathematical function है जिससे हम Time Complexity और number of comparisons के बारे मे अनुमान लगा सकते है। Recurrence का मतलब है दोबारा से घटित होना ।

नियम –

1. यदि समस्या का दिया गया उदाहरण छोटा या सरल है, तो बस इसे हल करें।
2. अन्यथा, समस्या को एक या अधिक, एक ही समस्या के सरल उदाहरणों तक कम करें।

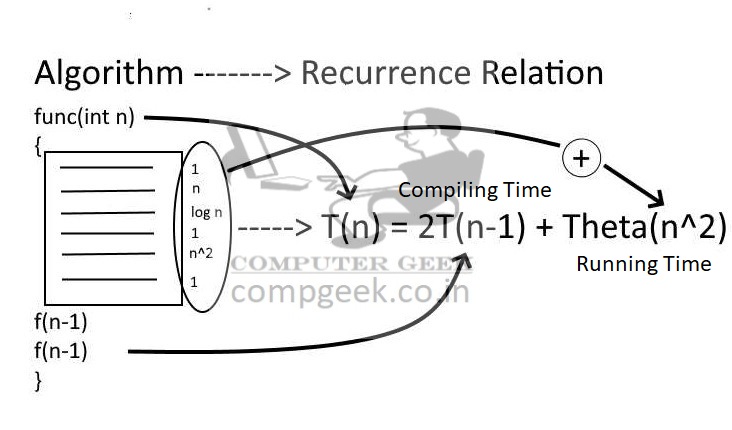
Code to Recurrence function

Algorithm 1

f1(int n)

{

  if (n <= 1 )

      return;

  f1(n-1);

}

Recurrence function – 

T(1) = Θ(1)

T(n) = T(n – 1) + Θ(1)

T(n – 1) is compiling time and Θ(1)  is running time.

Trial –

If n = 1, then T(1) = Θ(1)

If n = 2, then we find f(1)

Algorithm 2

f2(int n)

{

  if (n <= 1)

     return;

  f2(n/2);

}

Recurrence function – 

T(1) = Θ(1)

T(n) = T(n/2) + Θ(1)

T(n/2) is compiling time and Θ(1) is running time.