Analysis of Algorithm (Hindi)

Design & Analysis of Algorithm

Analysis of Algorithm

Introduction to Algorithm

Growth of Function

एक अल्गोरिथ्म का Analysis या जांच दो तरीकों से कि जा सकती है। एक तो इसमें लगने वाला ‘समय’ (Time) और दूसरा वह अल्गोरिथ्म कितनी ‘जगह’ (Space) लेती है ।

Time Complexity: – computer science में, time complexity, operating system द्वारा किए गए number of operations है।

Space Complexity: – किसी problem को हल करने के लिए कितनी आवश्यक जगह चाहिए या कितनी bits (number of bits) चाहिए, उसको space complexity कहते हैं ।

यदि हमारे पास किसी समस्या के लिए दो अल्गोरिथ्म A1 और A2 हैं, तो हम ये जानना चाहते हैं कि कौन सा अल्गोरिथ्म कम से कम समय लेता है। हमारी समस्या उस अल्गोरिथ्म द्वारा ली गई जगह space complexity नहीं है। आज की दुनिया में, space बहुत है मतलब की हमारी जरूरत से ज्यादा है । हमारी समस्या समय (Time) है। समय मूल्यवान है।

Worst Case Complexity – यह किसी समस्या को हल करने के लिए एक अल्गोरिथ्म द्वारा लिया गया अधिकतम समय है।

Best Case Complexity – यह किसी समस्या को हल करने के लिए अल्गोरिथ्म द्वारा लिया गया न्यूनतम समय है।

Average Case Complexity – इसकी complexity, Best case और Worst case के बीच में है। कभी-कभी ये best case के बराबर हो जाती है और कभी ये worst case के बराबर हो जाती है । Average case का मतलब है कि किसी समस्या को हल करने के लिए एक अल्गोरिथ्म द्वारा औसत समय कितना लिया जाता है।

Time Complexity of a code

Code	Number of Operations
int main()	1
{	1
int p = 1, sum = 0, n=10;	1
for (p=1; p<=n; p++) { sum = sum + p; }	n
printf(sum);	1

ऊपर वाले Table को देखिए । इसमें बायीं तरफ code की instruction है और दायीं तरफ ये बताया हुआ है की compiler उसे कितनी बार execute करेगा, मतलब number of operations जो compiler को उस instruction को execute करने में लगेंगे । एक instruction को execute करने के लिए मान लो की compiler को 1 sec लगता है, तो time complexity 1 sec हुई ।

Table में हर एक instruction की time complexity का sum होगा = 1 + 1 + 1 + n + 1 इसलिए, time complexity n + 4 के बराबर है । लेकिन हम constant को हटा देंगे । क्यों?

अगर n बहुत large है तो इसका मतलब है की constant की कोई बड़ी भूमिका नहीं है । इसलिए code की Time Complexity O(n) है ।

Analyze Complexities of Algorithm

एक problem के कई अल्गोरिथ्म होते हैं। मान लो कि हमें एक program लिखना है ‘To swap two numbers’, और हम ऐसा करने के लिए C programming language में दो program लिखते हैं। इसमें हम केवल Time Complexity को देख रहे हैं।

Code 1 – Swap(A,B,C)

Start
int main()
{
int A, B, C;
printf(“Enter the first number : “);
scanf(“%d”, &A);
printf(“Enter the second number : “);
scanf(“%d”, &B);
C = A;
A = B;
B = C;
printf(“After Swapping A : ”, A);
printf(“After Swapping B : “, B);
Stop

Code 2 – Swap(A, B)

int main()
{
int A, B;
printf(“Enter two numbers : “);
scanf(“%d %d”, &A, &B);
A = A*B;
B = A/B;
A = A/B;
printf(“After Swapping A : ”, A);
printf(“After Swapping B : “, B);

पहले हम code 1 को देखते हैं।

इसमें variable C का उपयोग करके A और B swap होते हैं। Code 1 के पीछे logic यह है कि A और B दो numbers हैं और हमारे पास temporary variable C भी है। मान लेते हैं की A की value 15 है और B की value 5 है। C की कोई value नहीं है। A = 15, B = 5, C = garbage value

अब हम A की value C variable में रख देंगे जैसे की 9^th instruction में कहा गया है। अब C की value भी 15 है।

अब B की value A में रखेंगे। A = 5, B = 5, C = 15

अब C की value हम B में रखेंगे। अब A = 5, B = 15, C = 15

इस program में कोई complex logic नहीं है, केवल सरल सामान्य ज्ञान शामिल है। हालांकि हमने extra space लिया है। एक int data type variable C, और यही इसकी space complexity है।

Code 2 में, हम कोई extra space नहीं लेंगे। ना ही कोई variable और ना ही कोई array । हम वही दो variable लेंगे A और B, और मान लीजिए कि A 3 के बराबर है और B 5 के बराबर है। A = 5 B = 15

अब हम दोनों variables को multiply करते हैं और result को variable A में पास करते हैं, जैसा कि 6^th instruction में है। A = 75 और B = 15

7^th instruction में, हम B के value को A / B के बराबर होने के लिए बदलते हैं, जिसके परिणामस्वरूप B का एक नया value 5 होता है। A = 75 और B = 5

अब हमें A variable के value को बदलना होगा, जो A/B के बराबर है, जो 75/5 के बराबर है, जो 15 के बराबर होता है। हमने values की अदला-बदली की। A = 15 और B = 5

Computer केवल addition को समझता है। इसलिए, कोड 2 में, यदि हम A और B को multiply करते हैं, तो हमें A value को B times जोड़ना होगा, जो 15 + 15 + 15 + 15 + 15 = 75 के बराबर होता है, और divison के लिए अधिक complex operations और time की आवश्यकता होती है।

अगर आप इन दोनों codes कि Time Complexity निकाले तो दोनों कि Time Complexity एक ही होगी । Constant time में दोनों solve हो रहे है पर हकीकत में Code 2 की Time Complexity Code 1 की तुलना में अधिक होगी। क्योंकि code 2 में हम number of operations ज्यादा कर रहे हैं।

यदि हम Space Complexity पर विचार करते हैं, तो Code 2 एक अच्छा अल्गोरिथ्म है क्योंकि इसके लिए अधिक variable की आवश्यकता नहीं होती है, हालांकि, अगर हम Time Complexity पर विचार करते हैं, तो Code 1 अच्छा है।

Find the time complexity of algorithm (Important)

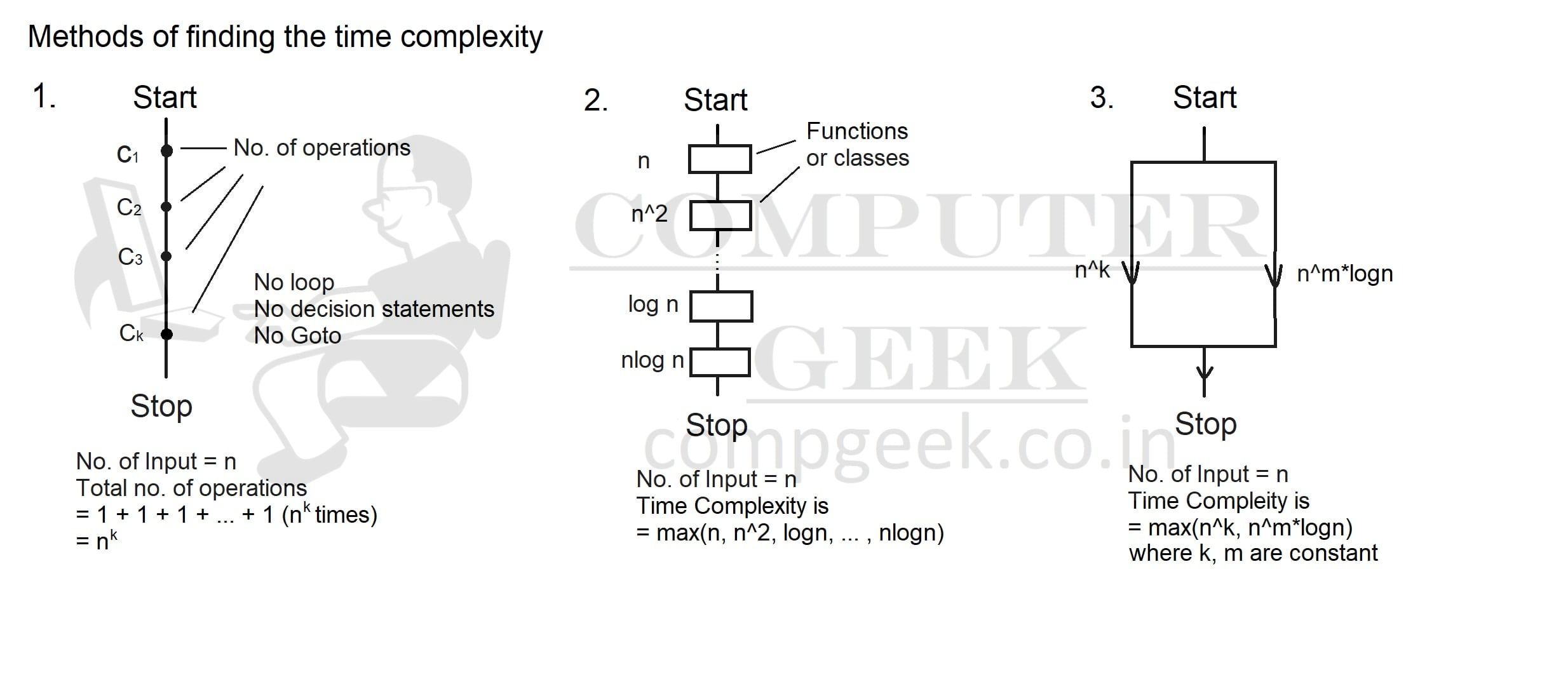
हमें ये पता है की time complexity असल में number of operations होते है और वो जिसमे ज़्यादा होंगे उसकी time complexity उतनी ही अधिक होगी।

हमारा code या अलगोरिथ्म एक sequence में होता है और ज़्यादातर उसमे decision statements भी होते हैं जो एक condition पर आधारित होते है। अगर condition true है तो एक statement पर compiler जाएगा और अगर वो false हैं तो दूसरी किसी statement पर जाएगा। कुछ loop भी होते है जैसे की for loop और while loop।

For loop की time complexity उसकी condition पर आधारित होती है । किसी भी loop में उसकी conditions बताती है की उसके number of operations कितने होंगे । While loop में भी conditions ही काम आतीं हैं ।

एक होता है recurrence theorem जो हम आगे पढ़ेंगे और उसकी Time Complexity को भी जानेंगे।

Test Yourself

Find the time complexity of code–

(A)

for (i = 1; i <= n; i++)
{

printf(“Hello”);
}

Answer

Time Complexity: is number of operations
In this code, I will take the value of i from 1 to n.
i = 1, print “hello”
i = 2, print “hello”
i = 3, print “hello”
…
…
i = n, print “hello”

i = n+1, condition becomes false

So, the code will print “hello” exactly n times and the time complexity is n+1. We remove the constant term and apply Big-Oh symbol. So, the Time complexity is O(n)

(B)

for(i = 1; i <= n; i++)

{
for(j = 1; j <= n; j++)

{

printf(“Hello”);

}
}

Answer

In this code,

i	j
1	1, 2, 3, ……, n
2	1, 2, 3, ……, n
3	1, 2, 3, ……, n
…..	……
…..	……
n	1, 2, 3, ……, n

means it will print “hello” for every j value.

so j value is 1 to n, for every ith value. i value is from 1 to n.

so, we have n*n operations. Time Complexity is O(n^2).

Note- Time complexity is Number of operations. So, j value is going to be from 1 to n+1. In n+1, its j value is false. Also, i value is going from 1 to n+1. So what i mean to say is that time complexity is (n+1)^2. But according to our rules, lower order term and constants are discarded. That is why, time complexity is O(n^2).

(C)

for(i = 1; i <= n; i++)
{
for(j = 1; j <= i; j++)
{
printf(“Hello”);
}
}

Answer

In this code

i	j
1	1
2	1, 2
3	1, 2, 3
…..	……
…..	……
n	1, 2, 3, ……, n

means it will print “hello” for every j value.

so, j values sum equal to

Sum = 1 + 2 + 3 + … + n = (n(n+1))/2

Sum = (n^2 + n)/2 = O(n^2) (We remove constants and lower-order term.)

(D)

for(i = 1; i <= n; i++)

{

for(j = 1; j<= n; j = j*2)

{

printf(“Hello”);

}

Answer

In this code,

i	j
1	1, 2, 4, …, k
2	1, 2, 4, …, k
3	1, 2, 4, …, k
…..	……
…..	……
n	1, 2, 4, …, k

2^k <= n

After every j’s value, the code will print “hello”.

so, # of operations is n*k [k = log n]

It means that time complexity is O(n log n).

(E)

for(i = 0; i <= n; i = i*2)

{

for(j = 0; j <= n; j = j*2)

{

printf(“Hello”);

}

Answer

In the previous question, we have seen that j = j*2 derives time complexity log n.

So, in this question, i value is from 1 to n and i = i*2, and in the nested loop j value is from 1 to n and j = j*2.

So, the code’s time complexity becomes O((log n)^2).

Q2- If we have two algorithms for a problem Algo1 & Algo2. Algo1 has time complexity of O(n) and has a space complexity of O(n). Algo2 has a time complexity of O(n*logn) and has a space complexity of O(1). Which algorithm will you choose?

Answer

Generally, we do not think about space. We only think about time. Algorithm has to be time-effective. Algo1 has time complexity O(n) which is less than the time complexity of algo2 O(n*logn). So, we will use Algo1.

Suppose there is an old version of a software in your laptop, and it uses very less space but time complexity is higher in comparison to a new version of the same software. But new version wants a higher space than the old version. What will you choose? Ultimately you will buy a new laptop with 1TB or 2TB space and has a RAM of 8GB or higher, and install the new version which costs you less time.
Note- If you want a space-efficient algorithm, you choose Algo2. But this will happen only in less cases.