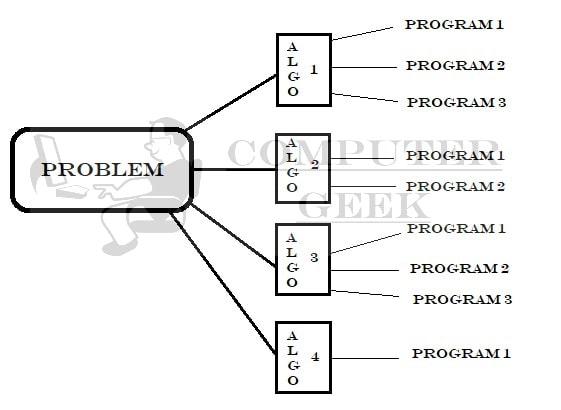एक problem में कई अल्गोरिथ्म हो सकते हैं और एक अल्गोरिथ्म में एक language के साथ-साथ विभिन्न languages के कई program हो सकते हैं।एक अच्छा अल्गोरिथ्म:

1. यह समय-कुशल होना चाहिए।
2. यह कम जगह का उपयोग करता है।
3. न्यूनतम संभव परिणामों (minimum possible result) में समस्याओं को हल करता है।
4. समाधान तक पहुंचने के लिए न्यूनतम संसाधन (minimum resources) का उपयोग करता है।
5. इसे आसानी से समझा जाना चाहिए ।
6. न्यूनतम लागत पर बनाए रखा जा सकता है।
7. यह लचीला होना चाहिए ।
8. सभी प्रकार के अपवादों और त्रुटियों (exceptions & errors) का प्रबंधन करता है।
9. आत्मनिर्भर है।
10. एक जैसी समस्याओं के लिए इसे लागू किया जा सकता है।
11. संतुलित होना चाहिए।

कोरमैन की किताब के मुताबिक, अल्गोरिथ्म एक तकनीक की तरह ही हैं। हम सभी नवीनतम और सबसे तेज़ processor का उपयोग करते हैं लेकिन हमें उस कंप्यूटर पर अच्छे अल्गोरिथ्म को चलाने की आवश्यकता है ताकि हम नवीनतम processor के लिए खर्च किए गए पैसे का ठीक से लाभ उठा सके।उदाहरण – एक fast computer A एक sorting अल्गोरिथ्म चला रहा है जिसका चलने का समय n² की तरह बढ़ता है (इसका मतलब है कि time complexity C*n² है) एक slow computer B एक sorting अल्गोरिथ्म चला रहा है जिसका चलने का समय n logn की तरह बढ़ता है (इसका मतलब है कि time complexity C*n logn है)। C एक constant है।उनमें से प्रत्येक computer को 10 लाख नंबरों के एक input को sort करना होगा। इनपुट n =10 लाख numbers = 10⁶ numbers है ।

Computer A	Computer B
1 second में 100 crore instruction हल करता है = 109/sec	1 second में 1 crore instruction हल करता है  = 107/sec
Algorithm time complexity = n2 instructions	Algorithm time complexity = 25*nlogn instructions
समय लगा  = n2/ (execute instructions in a sec) = (106)2/109	समय लगा  = n log n / (execute instructions in a sec) = 25*(106 log106)/107
इसमें लगे 16.66 minutes	इसमें लगे 15 seconds

धीमे कंप्यूटर दौड़ जीत सकते हैं । जैसे की कछुए ज़्यादातर खरगोश से जीतते हैं।