A two-way finite automaton is called two-way because its input head can move in both directions, left as well as right, on the input tape. It does not have two heads, and the term does not mean two different types of automata. The defining feature is only the bi-directional movement of the read head. Therefore, the correct answer is option 3.
Menu
Unit 1
Overview: Automata, Computability and Complexity, Alphabet, Symbol, String, Formal Languages.
Q21 – If ∑ = {a, b, c, d, e, f} then number of strings in ∑ of length 4 such that no symbol is used more than once in a string is
35
360
49
720
Ans – (2)
Explanation –
We are given the alphabet Σ = {a, b, c, d, e, f}.
So, there are total 6 different symbols.
We have to find the number of strings of length 4, with the condition that no symbol is repeated in any string.
First, we choose 4 different symbols out of the given 6 symbols.
The number of ways to choose these symbols is 15.
After selecting 4 symbols, we can arrange them in different orders to form different strings.
The number of possible arrangements of 4 symbols is
4! = 24.
So, total number of valid strings
= 15 × 24
= 360.
Therefore, the correct answer is option 2 – 360.
Q22 – The transitions which does not take an input symbol are called
ε-transitions
λ-transitions
Both of the mentioned
None
Ans – (3)
Explanation –
In automata theory, sometimes a transition happens without reading any input symbol from the input string. Such transitions move from one state to another automatically.
These transitions are commonly called ε-transitions.
In many books, the same type of transition is also called a λ-transition.
So, ε-transition and λ-transition mean the same thing – a transition that does not consume any input symbol.
Therefore, the correct answer is option 4 – Both of the mentioned.
Q23 – Which of the following strings can be obtained by the language L = {aib2i | i≥ 1}?
aaabbbbbb
aabbb
abbabbba
aaaabbbabb
Ans – (1)
Explanation – Here, number of a’s = 3
So, 2i = 2 × 3 = 6 b’s
The string has 3 a’s followed by 6 b’s, so it follows the rule.
Q24 – Give a production grammar for the language L = {x/x ∈ (a,b)*, the number of a’s in x is multiple of 3}.
{S->bS, S->b, S->aA, S->bA, A->aB, B->bB, B->aS, S->a}
{S->aS, S->bA, A->bB, B->bBa, B->bB}
{S->aaS, S->bbA, A->bB, B->ba}
None of the above
Ans – (3)
Explanation –
This means –
The string can contain a and b in any order
But the count of a’s must be 0, 3, 6, 9, …
b’s do not affect the condition
To design a grammar for this language, we usually think in terms of states:
S – number of a’s ≡ 0 (mod 3) → valid state
A – number of a’s ≡ 1 (mod 3)
B – number of a’s ≡ 2 (mod 3)
Now check option 1, this cycle ensures that every 3 a’s bring us back to S, so the total number of a’s is a multiple of 3.
Also, productions with B allow b to appear anywhere without changing the count of a’s.
Q25 – Which of the following strings is NOT in the Kleene star of the language {011, 10, 110}?
10110
01110
110011
0111110
Ans – (4)
Explanation –
First, understand what Kleene star means.
L* means-
We can take zero or more strings from the set {011, 10, 110}
And concatenate them in any order
Empty string is also allowed
Option 4 is the correct answer.
Q26 – CFG is
Compiler
A language expression
Regular Expression
None of the mentioned
Ans – (2)
Explanation –
CFG stands for Context-Free Grammar.
A CFG is used to describe or define a language, especially programming languages and syntactic structures. It tells us how strings of a language can be generated using variables, terminals, and production rules.
Q27 – The idea of an automation with a stack as auxiliary storage
Finite automata
Push Down Automata
Deterministic Automata
None of the mentioned
Ans – (2)
Explanation – An automaton that uses a stack as auxiliary storage is called a Push Down Automaton (PDA).
The stack helps the automaton remember extra information, such as nested structures, which finite automata cannot handle.
Q28 – A FA can be used for
String recognition
Arithmetic operations
Both a and b
None of these
Ans – (1)
Explanation –
A Finite Automaton (FA) is mainly used to recognize or accept strings that belong to a particular language.
It reads an input string symbol by symbol and checks whether the string follows the rules of the language.
Q29 – The palindromes can’t be recognized by a FA because
A FA can’t determine the midpoint of a palindrome
A FA can’t remember its previous input
A FA head has read only capability and can’t move in both directions
both 1 and 2
Ans – (1, 2)
Explanation –
A palindrome is a string that reads the same forward and backward.
A Finite Automaton (FA) cannot recognize palindromes because:
A FA cannot determine the midpoint of the input string. Without knowing the middle, it cannot compare the first half with the second half.
A FA cannot remember previous input symbols because it has only finite memory.
Both of these limitations make palindrome recognition impossible for FA. So option is 4. Both 1 and 2.
Q30 – Transition of finite automata is
Finite Diagram
State Diagram
Node Diagram
E-R Diagram
Ans – (2)
Explanation –
In a Finite Automaton, transitions show how the automaton moves from one state to another on reading input symbols.
These transitions are represented using a state diagram, where:
Circles represent states
Arrows represent transitions between states
Q31 – A context-free language is said to be ambiguous if
there exists a string w ∈ L(G) that has more than one leftmost derivation
there exists a string w ∈ L(G) that has more than one parse tree
both of the above
none of the above
Ans – (3)
Explanation –
A context-free language is called ambiguous when at least one string in the language can be generated in more than one way.
This can happen in two equivalent forms:
The string has multiple leftmost derivations, or
The string has multiple parse trees
Q32 – In computer, finite automata program can be stored using
Table
Two – dimensional array
Graph
All of the above
Ans – (4)
Explanation –
finite automaton program can be stored in a computer in different ways.
It can be stored in a table form, where rows represent states and columns represent input symbols.
The same table can be implemented using a two-dimensional array in programming.
It can also be represented as a graph, where states are nodes and transitions are edges.
Q33 – Finite automation and FSMS are used for
Pattern matching
Sequential circuit design
Compiler design
All of the above
Ans – (4)
Explanation –
Finite Automata (FA) and Finite State Machines (FSMs) are very useful models in computer science and engineering.
They are used in pattern matching, such as searching text or validating input formats.
They are used in sequential circuit design, where the system behavior depends on the current state and inputs.
They are also used in compiler design, especially in lexical analysis to recognize tokens.
Q34 – Which of the following identity is wrong?
R + R = R
(R*)* = R*
(R*)* = R*
ØR = RØ = RR*
Ans – (4)
Explanation – The identity R + R = R is correct because the union of a language with itself does not change the language. The identity (R*)* = R* is also correct since applying the Kleene star more than once has no additional effect, and that is why options b and c are valid. However, option 4 is wrong because concatenating the empty language Ø with any language always results in Ø, so ØR = Ø and RØ = Ø. On the other hand, RR* is generally not the empty language. Therefore, equating ØR, RØ, and RR* is incorrect, making option 4 the wrong identity.
Q35 – Finite automata has
Finite memory
Read only head
Finite control
All of the above
Ans – (4)
Explanation – A finite automaton has finite memory, which means it can remember only a limited amount of information using its states.
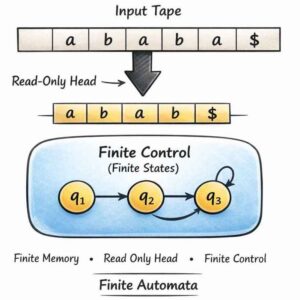
It also has a read-only input head, so it can only read the input symbols and cannot modify them or move backward. In addition, it has finite control, meaning it operates with a finite number of states that control its behavior.
Q36 – Two – way finite automata has
Two types
Two heads
Bi – directional head movement
All the above
Ans – (3)
Explanation –
Q37 – A FA with deterministic transitions capability is known as
NFA
DFA
FA
NFA with ε – moves
Ans – (2)
Explanation – Deterministic Finite Automata (DFA).
Q38 – A FA with non – deterministic transitions capability is known as
NFA
DFA
2DFA
NFA with ε – moves
Ans – (1)
Explanation – A finite automaton with non-deterministic transition capability is called a Non-Deterministic Finite Automaton (NFA).
Q39 – How many DFA’s exist with three states over the input alphabet {0,1}?
144
6561
5832
729
Ans – ()
Explanation – The table shows a DFA with three states X, Y, and Z and input alphabet {0, 1}. For each state and for each input symbol, the transition can go to any one of the three states. Since there are 3 states and 2 input symbols, we have 6 transitions in total, and each transition has 3 choices, giving 3^6 possibilities. In addition to the transition function, each state can independently be chosen as a final or non-final state, so for 3 states there are 2^3 possible choices of final states. Multiplying these together gives 3^6×2^3=5832 possible DFAs for a fixed start state. If we fix the start state as X, we get 5832 DFAs. Similarly, if Y is the start state, we again get 5832 DFAs, and the same holds when Z is the start state. Since the start state can be chosen in 3 different ways, the total number of DFAs becomes 3 × 5832 = 17496.
Q40 – Limitation of a FA is
Writing
Finite memory
Pattern recognition
Both (1) and (2)
Ans – (4)
Explanation – A finite automaton (FA) has some clear limitations. First, it cannot write or modify the input, because it has a read-only input head. Second, it has finite memory, which means it can remember only a limited amount of information using its finite number of states. Because of this limited memory, an FA cannot solve problems that require remembering an unbounded amount of past input.





