SYLLABUS
ER‐model. Relational model: relational algebra, tuple calculus, SQL. Integrity constraints, normal forms. File organization, indexing (e.g., B and B+ trees). Transactions and concurrency control.
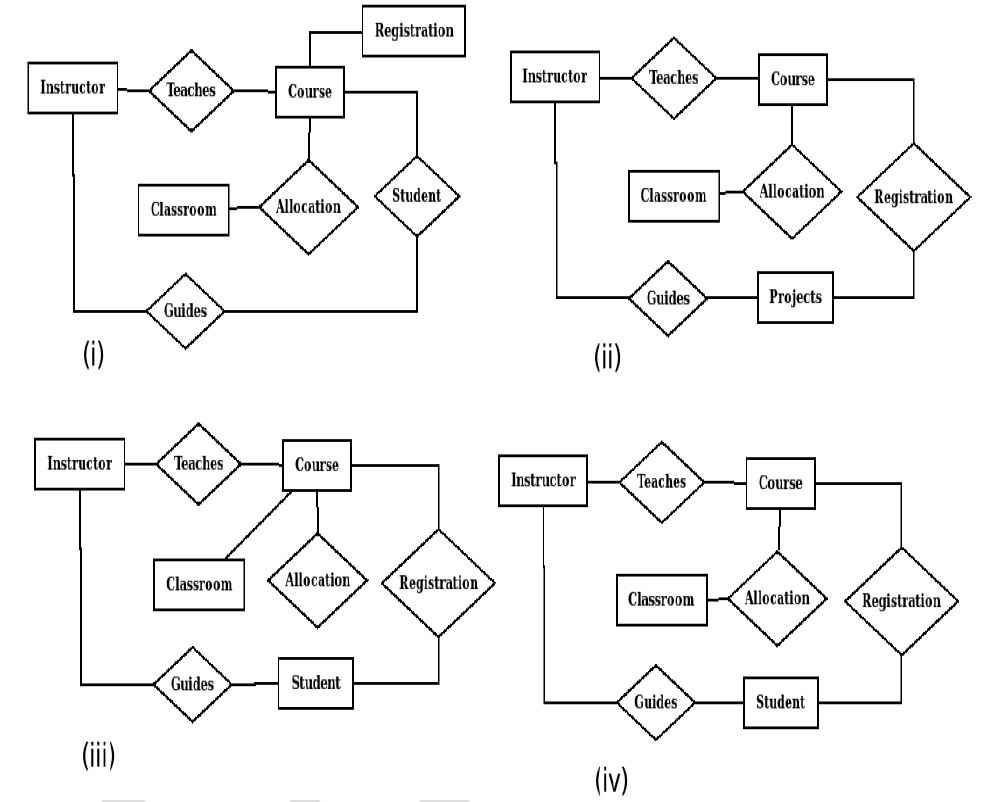
Q1 – Let S be the specification: “Instructors teach courses. Students register for courses. Courses are allocated classrooms. Instructors guide students.” Which one of the following ER diagrams CORRECTLY represents S?
 (A) (i)
(A) (i)
(B) (ii)
(C) (iii)
(D) (iv)
Ans – (D)
Explanation –
Four relationships are there
- Instructor(Rectangle) —– Teaches(diamond) —- Course(Rectangle) – Absent in None
- Student(Rectangle) —- Registers(Diamond) —- Course(Rectangle) – Absent in (i) and (ii)
- Course(Rectangle) —- Allocated(Diamond) —- Classroom(Rectangle) – Absent in (iii)
- Instructor(Rectangle) —- Guides(Diamond) —- Student(Rectangle) – Absent in (i) and (ii)
So, option D is the answer.
Q2 – Which of the following statements about a relation R in first normal form (1NF) is/are TRUE ?
(A) R can have a multi-attribute key
(B) R cannot have a foreign key
(C) R cannot have a composite attribute
(D) R cannot have more than one candidate key
Ans – (A, C)
Explanation – First Normal Form (1NF) requires a relation to contain only atomic (indivisible) values in each cell and have no repeating groups or arrays.
According to the rules of 1NF, a relation can have a multi-attribute key (or composite key), which means that more than one attribute can be used to identify the row uniquely. Thus, statement (A) is true.
A relation cannot have a composite attribute in 1NF because all composite attributes (e.g., a “Name” field that contains first names and last names) must be decomposed into atomic attributes. Thus, statement (C) is true as well.
However, a relation in 1NF can have a foreign key. So, both statements (B) and (D) are false because 1NF has no restrictions on the presence of foreign keys, nor does 1NF have any restrictions on having more than one candidate key. Therefore, only statements (A) and (C) are true.
Q3 – Consider the following two relations, R(A,B) and S(A,C):
R S
A B A C
10 20 10 90
20 30 30 45
30 40 40 80
30 50
50 95
The total number of tuples obtained by evaluating the following expression 𝝈𝑩<𝑪 (𝑹⋈𝑹.𝑨=𝑺.𝑨 𝑺) is _________.
Ans – (2)
Explanation –
Perform a natural join on R.A = S.A
R | S | ||
A | B | A | C |
10 | 20 | 10 | 90 |
30 | 40 | 30 | 45 |
30 | 50 | 30 | 45 |
Apply Condition B < C
R | S | ||
A | B | A | C |
10 | 20 | 10 | 90 |
30 | 40 | 30 | 45 |
The total number of tuples obtained by evaluating the following expression 𝝈𝑩<𝑪 (𝑹⋈𝑹.𝑨=𝑺.𝑨 𝑺) is 2.
Q4 – The symbol → indicates functional dependency in the context of a relational database.
Which of the following options is/are TRUE?
(A) (𝑋,𝑌) → (𝑍,𝑊) implies 𝑋 → (𝑍,𝑊)
(B) (𝑋,𝑌) → (𝑍,𝑊) implies (𝑋,𝑌) → 𝑍
(C) ((𝑋,𝑌) → 𝑍 and 𝑊 → 𝑌) implies (𝑋,𝑊) → 𝑍
(D) (𝑋 → 𝑌 and 𝑌 → 𝑍) implies 𝑋 → 𝑍
Ans – (B, C, D)
Explanation –
In relational databases, a functional dependency (FD) uses the notation → to indicate that one set of attributes uniquely determines another. For example, if X → Y, it indicates that knowing the value of X is sufficient to know the value of Y.
Option (A) statement is not necessarily true because it takes the combination of both X and Y to determine Z and W. Knowing only X may not be sufficient.
Option (B) is true due to the decomposition rule of functional dependencies, because when a group of attributes determines another group of attributes, it must also determine every single attribute in that group.
Option (C) is true because through W we can determine Y, and now with X we determine Z. This follows from the properties of transitivity and augmentation of functional dependencies.
Option (D) states that if X → Y and Y → Z, then X → Z. This is a well-known transitivity rule, and it is true.



 (A) (i)
(A) (i)