SYLLABUS
Regular expressions and finite automata. Context-free grammars and push-down automata.Regular and contex-free languages, pumping lemma. Turing machines and undecidability.
Q1 – Let 𝐿1, 𝐿2 be two regular languages and 𝐿3 a language which is not regular. Which of the following statements is/are always TRUE?
(A) 𝐿1 = 𝐿2 if and only if 𝐿1∩ 𝐿2̅ =𝜙
(B) 𝐿1 ∪ 𝐿3 is not regular
(C) 𝐿3̅ is not regular
(D) 𝐿1̅ ∪ 𝐿2̅ is regular
Ans – (C, D)
Explanation – Let L1 and L2 be two regular languages, and L3 be a language that is not regular.
(A) says that L1 = L2 if and only if L1 ∩ complement of L2 = ∅. This is not always true because this would only prove one direction of set equality. To prove that L1 = L2 we must prove that L2 ∩ complement of L1 = ∅. Thus, (A) is false.
(B) says that L1 ∪ L3 is not regular. This is not always true. The union of a regular and non-regular language can be either regular or non-regular depending on the specific structure of L3. Therefore, (B) is not always true.
(C) states the complement of a non-regular language (L3) is not regular. This is always true because regular languages are closed under complementation. If the complement is regular, the original language must also be regular resulting in contradiction.
(D) states the union of the complements of two regular languages is regular. This is always true because regular languages are closed under both complement and union.
Q2 – Consider the 5-state DFA 𝑀 accepting the language 𝐿(𝑀) ⊂ (0+1)* shown below. For any string 𝑤∈(0+1)* let 𝑛0(𝑤) be the number of 0′𝑠 in 𝑤 and 𝑛1(𝑤) be the number of 1′𝑠 in 𝑤.
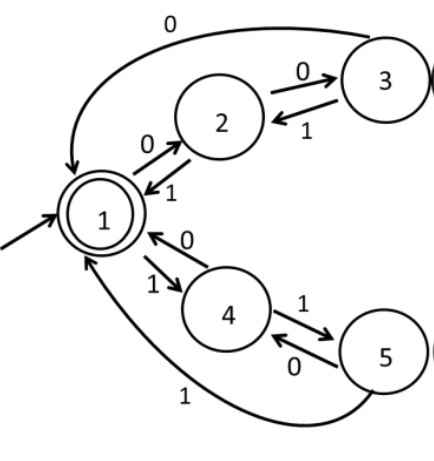
Which of the following statements is/are FALSE?
(A) States 2 and 4 are distinguishable in 𝑀
(B) States 3 and 4 are distinguishable in 𝑀
(C) States 2 and 5 are distinguishable in 𝑀
(D) Any string 𝑤 with 𝑛0(𝑤)=𝑛1(𝑤) is in 𝐿(𝑀)
Ans – (B, C)
Explanation – In order to check for distinguishability between two states, we try to be able to generate a string that starts at both states and leads to two different outcomes differentiated by one outcome leading to an accepting state and the other leading to a non-accepting state.
Option (A) – States 2 and 4 are distinguishable
For input 0 – State 2 -> State 3 (non-accepting state)
For input 0 – State 4 -> State 1 (accepting state)
For input 1 – State 2 -> State 1 (accepting state)
For input 1 – State 4 -> State 5 (non-accepting state)
This is true.
Option (B) – States 3 and 4 are distinguishable
For input 0 – State 3 -> State 1 (accepting state)
For input 0 – State 4 -> State 1 (accepting state)
For input 1 – State 3 -> State 2 (non-accepting state)
For input 1 – State 4 -> State 5 (non-accepting state)
This is False.
Option (C) – States 2 and 5 are distinguishable
For input 0 – State 2 -> State 3 (non-accepting state)
For input 0 – State 5 -> State 4 (non-accepting state)
For input 1 – State 2 -> State 1 (accepting state)
For input 1 – State 5 -> State 1 (accepting state)
This is False.
Option (D) – Any string 𝑤 with 𝑛0(𝑤)=𝑛1(𝑤) is in 𝐿(𝑀)
For input 01 – State 1 -> State 2 -> State 1
For input 0011 – State 1 -> State 2 -> State 3 -> State 2 -> State 1
For input 1100 – State 1 -> State 4 -> State 5 -> State 4 -> State 1
This is true.
Q3 – Let 𝐺 = (𝑉, Σ, 𝑆, 𝑃) be a context-free grammar in Chomsky Normal Form with Σ = {𝑎, 𝑏, 𝑐} and 𝑉 containing 10 variable symbols including the start symbol 𝑆. The string 𝑤 = 𝑎30𝑏30𝑐30 is derivable from 𝑆. The number of steps (application of rules) in the derivation 𝑆→*𝑤 is _________.
Ans – (179)
Explanation – The grammar generates the string w = a³⁰b³⁰c³⁰, which is 90 characters long.
Every production rule in CNF is of the form A → BC (where A, B, and C are variables), or A → a (where a is the terminal symbol).
Since we need to generate 90 terminal symbols (30 a’s, 30 b’s, and 30 c’s), we will need to have 90 applications of rules such as A → a, one for each terminal.
To the parse tree derivation, we need a binary tree which combines all variables together. A binary tree with 90 leaves (terminals) needs 89 internal nodes, which means we need 89 applications of the rules such as A → BC.
Thus, the number of total steps in the derivation is 90 (terminals) + 89 (internal nodes) = 179 steps.
Q4 – Consider the following two regular expressions over the alphabet {0, 1}:
𝑟 = 0*+1*
𝑠 = 01*+10*
The total number of strings of length less than or equal to 5, which are neither in 𝑟 nor in 𝑠, is _________.
Ans – (44)
Explanation – The total number of strings of length less than or equal to 5 over the alphabets {0, 1} is = 1 + 2 + 4 + 8 + 16 + 32 = 63 strings.
Strings in r = 0* + 1* = ϵ, 0, 00, 000, 0000, 00000, 1, 11, 111, 1111, 11111. There is total 11 strings.
Strings in s = 01* + 10* = 0, 01, 011, 0111, 01111, 1, 10, 100, 1000, 10000. There is total 10 strings
Strings in r and s = 11 + 10 – 2 = 19 strings [because 0 and 1 strings are in both r and s]
The total number of strings of length less than or equal to 5, which are neither in 𝑟 nor in 𝑠, is 63 – 19 = 44 strings.


