SYLLABUS
(i) Supervised Learning: regression and classification problems, simple linear regression, multiple linear regression, ridge regression, logistic regression, k-nearest neighbour, naive Bayes classifier, linear discriminant analysis, support vector machine, decision trees, biasvariance trade-off, cross-validation methods such as leave-one-out (LOO) cross-validation, k-folds cross-validation, multi-layer perceptron, feed-forward neural network;
(ii) Unsupervised Learning: clustering algorithms, k-means/k-medoid, hierarchical clustering, top-down, bottom-up: singlelinkage, multiple-linkage, dimensionality reduction, principal component analysis.
Q1 – Consider the dataset with six datapoints: {(𝒙𝟏, 𝒚𝟏), (𝒙𝟐, 𝒚𝟐), … ,(𝒙𝟔, 𝒚𝟔)}, where
 and the labels are given by 𝒚𝟏 = 𝒚𝟐 = 𝒚𝟓 = 1, and 𝒚𝟑 = 𝒚𝟒 = 𝒚𝟔 = −1. A hard margin linear support vector machine is trained on the above dataset.
and the labels are given by 𝒚𝟏 = 𝒚𝟐 = 𝒚𝟓 = 1, and 𝒚𝟑 = 𝒚𝟒 = 𝒚𝟔 = −1. A hard margin linear support vector machine is trained on the above dataset.
Which ONE of the following sets is a possible set of support vectors?
(A) {𝒙𝟏, 𝒙𝟐, 𝒙𝟓}
(B) {𝒙𝟑, 𝒙𝟒, 𝒙𝟓}
(C) {𝒙𝟒, 𝒙𝟓}
(D) {𝒙𝟏, 𝒙𝟐, 𝒙𝟑, 𝒙𝟒}
(GATE DS&AI 2024)
Ans – (D)
Explanation – In a hard margin SVM, the support vectors are placed on the boundary between the margins (i.e., they are closest to the decision boundary but correctly classified). For the farther points, which are located inside their class region, the centre of the margin, they are not support vectors.
Now x1 = [1, 0], y1 = 1 is closest to the decision boundary.
Then x2 = [0, 1], y2 = 1 is closest to the decision boundary.
x3 = [0, -1], y3 = -1 is closest to the decision boundary.
x4 = [-1, 0], y4 = -1 is closest to the decision boundary.
Both x5 and x6 is far from the decision boundary, so they are not support vectors. Hence option D is the answer.
Q2 – Match the items in Column 1 with the items in Column 2 in the following table:
Column 1
(p) Principal Component Analysis
(q) Naïve Bayes Classification
(r) Logistic Regression
Column 2
(i) Discriminative Model
(ii) Dimensionality Reduction
(iii) Generative Model
(A) (p) − (iii), (q) − (i), (r) − (ii)
(B) (p) − (ii), (q) − (i), (r) − (iii)
(C) (p) − (ii), (q) − (iii), (r) − (i)
(D) (p) − (iii), (q) − (ii), (r) − (i)
(GATE DS&AI 2024)
Ans – (C)
Explanation – (p) Principal Component Analysis → (ii) Dimensionality Reduction
Principal Component Analysis (PCA) is a tool to lower the dimensional space of a huge data set by converting them into a smaller set of variables that still have most of the information contained in them.
(q) Naïve Bayes Classification → (iii) Generative Model
Naïve Bayes model is a kind of generative model that finds the joint probability spread of and then uses Bayes’ theorem to assess the conditional probability.
(r) Logistic Regression → (i) Discriminative Model
Logistic Regression, on the other hand, is a discriminative model that in contrast straightly estimates the conditional probability p(y∣x) without reference to the distribution of x.
Q3 – Euclidean distance based 𝑘-means clustering algorithm was run on a dataset of 100 points with 𝑘=3. If the points [1; 1] and [−1; 1] are both part of cluster 3, then which ONE of the following points is necessarily also part of cluster 3?
(A) [0; 0]
(B) [0; 2]
(C) [2; 0]
(D) [0; 1]
(GATE DS&AI 2024)
Ans – (D)
Explanation – The k-means algorithm is run using Euclidean distance.
k=3, and cluster 3 contains the points x1 = [1; 1], x2 = [-1; 1]
Centroid is the mean of all points in the cluster.
Centroid = ½([1; 1] + [-1; 1]) = ½([1+(-1); 1+1] = ½([0; 2] = [0; 1]
We now compute Euclidean distance from each option to the centroid [0; 1]
Option A – [0; 0]
Distance = √((0-0)2 + (0-1)2 = √1 = 1
Option B – [0; 2]
Distance = √((0-0)2 + (2-1)2 = √1 = 1
Option C – [2; 0]
Distance = √((2-0)2 + (0-1)2 = √(4 + 1) = √5
Option D – [0; 1]
Distance = √((0-0)2 + (1-1)2 = √0 = 0
So, option D is the closest and necessary part of the cluster 3.
Q4 – Given a dataset with 𝐾 binary-valued attributes (where 𝐾 > 2) for a two-class classification task, the number of parameters to be estimated for learning a naïve Bayes classifier is
(A) 2𝐾 + 1
(B) 2𝐾 + 1
(C) 2𝐾+1 + 1
(D) 𝐾2 + 1
(GATE DS&AI 2024)
Ans – (B)
Explanation – If there are 2 classes (such as class 0 and class 1), we will need 2 probabilities per attribute, that is, a total of 2K parameters for K binary valued attributes. Moreover, it is necessary to calculate the prior probability of one class (e.g. P(Class = 1)), as the prior probability of the other class can be recovered by subtracting this value from one. To sum up, one class prior only needs to be computed, thus the number of the parameters is increased by 1. In total, that is 2K+1 parameters that should be estimated.
Q5 – For any binary classification dataset, let 𝑆𝐵 ∈ ℝ𝑑×𝑑 and 𝑆𝑊 ∈ ℝ𝑑×𝑑 be the between-class and within-class scatter (covariance) matrices, respectively. The Fisher linear discriminant is defined by 𝑢∗ ∈ ℝ𝑑, that maximizes
𝐽(𝑢) = 𝑢𝑇𝑆𝐵𝑢/𝑢𝑇𝑆𝑊𝑢
If 𝜆 = 𝐽(𝑢∗), 𝑆𝑊 is non-singular and 𝑆𝐵 ≠ 0, then (𝑢∗, 𝜆) must satisfy which ONE of the following equations?
Note: ℝ denotes the set of real numbers.
(A) 𝑆𝑊−1 𝑆𝐵𝑢∗ =𝜆𝑢∗
(B) 𝑆𝑊𝑢∗ = 𝜆𝑆𝐵𝑢∗
(C) 𝑆𝐵𝑆𝑊𝑢∗ = 𝜆𝑢∗
(D) 𝑢∗𝑇𝑢∗ = 𝜆2
(GATE DS&AI 2024)
Ans – (A)
Explanation – This question is specifically from a method called Fisher Linear Discriminant Analysis (LDA). It is used to separate two classes (binary classification).
You are given two important matrices
- SB – Between-class scatter – tells how far the two classes are from each other.
- SW – Within-class scatter – tells how spread out the data points are within each class.
Both matrices are size d × d, where d is the number of features.
We want to find a direction u (a vector) such that
- The distance between classes is large (good separation),
- The spread inside each class is small (less confusion).
This is done using a formula called Fisher’s criterion 𝐽(𝑢) = 𝑢𝑇𝑆𝐵𝑢/𝑢𝑇𝑆𝑊𝑢. It is a ratio of the class separation by noise or spread inside class. We want to find the best vector u* that gives the maximum value of J(u). This vector is the best direction to separate the two classes.
The answer is option (A) 𝑆𝑊−1 𝑆𝐵𝑢∗ =𝜆𝑢∗. This is a standard result in linear algebra. It means u* is an eigenvector of the matrix 𝑆𝑊−1 𝑆𝐵, and λ is its eigenvalue.
Q6 – Consider the table below, where the (𝑖,𝑗)𝑡ℎ element of the table is the distance between points 𝑥𝑖 and 𝑥𝑗. Single linkage clustering is performed on data points, 𝑥1, 𝑥2, 𝑥3, 𝑥4, 𝑥5.
𝑥1 | 𝑥2 | 𝑥3 | 𝑥4 | 𝑥5 | |
𝑥1 | 0 | 1 | 4 | 3 | 6 |
𝑥2 | 1 | 0 | 3 | 5 | 3 |
𝑥3 | 4 | 3 | 0 | 2 | 5 |
𝑥4 | 3 | 5 | 2 | 0 | 1 |
𝑥5 | 6 | 3 | 5 | 1 | 0 |
Which ONE of the following is the correct representation of the clusters produced?

(GATE DS&AI 2024)
Ans – (A)
Explanation – In this table, what is the minimum distance from one node to another node, it is 1.
(x1 distance to x2 and vice versa) = 1
Also, (x4 distance to x5 and vice versa) = 1
So, they are closely forming a new cluster.
First cluster is – (x1, x2)
Second cluster is – (x4, x5)
Option C and D are ruled out because they are not forming a cluster between x4 and x5.
Min. Distance | (x1, x2) | (x3) | (x4, x5) |
(x1, x2) | 0 | 3 | 3 |
(x3) | 3 | 0 | 2 |
(x4, x5) | 3 | 2 | 0 |
The minimum distance is 2.
(x3 distance to x4 and vice versa) = 2
So, x3 will build a new cluster with x4, and x4 and x5 already made a cluster, so its representation is (x3, (x4, x5)).
Option B is also ruled out because they are forming a cluster between ((x1, x2), x3).
Min. Distance | (x1, x2) | (x3, (x4, x5)) |
(x1, x2) | 0 | 3 |
(x3, (x4, x5)) | 3 | 0 |
The minimum distance is 3.
((x1, x2) distance to (x3, (x4, x5)) and vice versa) = 3
So, (x1, x2) will build a new cluster with (x3, (x4, x5)) and its representation is ((x1, x2), (x3, (x4, x5))).
Hence option A is the answer.
Q7 – Consider the two neural networks (NNs) shown in Figures 1 and 2, with 𝑅𝑒𝐿𝑈 activation (𝑅𝑒𝐿𝑈(𝑧) = max{0, 𝑧}, ∀𝑧 ∈ ℝ). ℝ denotes the set of real numbers. The connections and their corresponding weights are shown in the Figures. The biases at every neuron are set to 0. For what values of 𝑝, 𝑞, 𝑟 in Figure 2 are the two NNs equivalent, when 𝑥1, 𝑥2, 𝑥3 are positive?
Figure 1
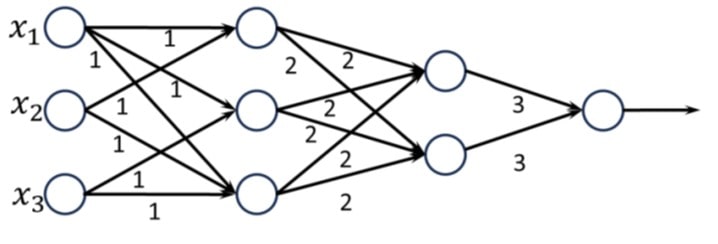
Figure 2

(A) 𝑝=36, 𝑞=24, 𝑟=24
(B) 𝑝=24, 𝑞=24, 𝑟=36
(C) 𝑝=18, 𝑞=36, 𝑟=24
(D) 𝑝=36, 𝑞=36, 𝑟=36
(GATE DS&AI 2024)
Ans – (A)
Explanation – While one is a big and complex neural network (Figure 1), the other one is small and simple (Figure 2). Both of them require three inputs x1, x2, x3.
Also, they will both give the same final output.
They both are applying ReLU activation. As for ReLU, the abbreviation from Rectified Linear Unit is used. While the input is a positive value, ReLU is a function that follows the straight y=x line, so the return value will be the same. If the input is a zero value or a negative one, then ReLU gives zero back.
Furthermore, the bias of all the neurons is 0. bias is just a number to which the sum of the inputs is being added. That is, there are no biases.
Furthermore, there are 6 paths leading from x1 to the output.
Each path provides the following set of weights “1 (from x to 1st layer) + 2 (from 1st layer to 2nd layer) + 3 (from 2nd layer to final output) = 6 weight.
So the overall contribution from x1 (means p in figure 2) to the output is 6×6 = 36.
At the same time, there are 4 ways leading from x2 to the output.
Each path provides 6 weight.
So the overall contribution from x2 (means q in figure 2) to the output is 4×6 = 24.
At the same time, there are 4 ways leading from x3 to the output.
Each path provides 6 weight.
So the overall contribution from x3 (means r in figure 2) to the output is 4×6 = 24.
Q8 – Consider the following figures representing datasets consisting of two-dimensional features with two classes denoted by circles and squares.

Which of the following is/are TRUE?
(A) (i) is linearly separable.
(B) (ii) is linearly separable.
(C) (iii) is linearly separable.
(D) (iv) is linearly separable.
(GATE DS&AI 2024)
Ans – (A, D)
Explanation – Option A – (i) and option D – (iv) are linearly separable because a line can separate the circles and squares.

Q9 – Details of ten international cricket games between two teams “Green” and “Blue” are given in Table C. This table consists of matches played on different pitches, across formats along with their winners. The attribute Pitch can take one of two values: spin-friendly (represented as 𝑆) or pace-friendly (represented as 𝐹). The attribute Format can take one of two values: one-day match (represented as 𝑂) or test match (represented as 𝑇).
A cricket organization would like to use the information given in Table C to develop a decision-tree model to predict outcomes of future games between these two teams.
To develop such a model, the computed InformationGain(C, Pitch) with respect to the Target is ______ (rounded off to two decimal places).
Table C Match Number | Pitch | Format | Winner (Target) |
1 | 𝑆 | 𝑇 | Green |
2 | 𝑆 | 𝑇 | Blue |
3 | 𝐹 | 𝑂 | Blue |
4 | 𝑆 | 𝑂 | Blue |
5 | 𝐹 | 𝑇 | Green |
6 | 𝐹 | 𝑂 | Blue |
7 | 𝑆 | 𝑂 | Green |
8 | 𝐹 | 𝑇 | Blue |
9 | 𝐹 | 𝑂 | Blue |
10 | 𝑆 | 𝑂 | Green |
(GATE DS&AI 2024)
Ans – (0.12 to 0.13)
Explanation –
Entropy of Winner
Total Events =10
P(Green) = 4/10
P(Blue) = 6/10
Entropy = -[4/10*log2(4/10) + 6/10*log2(6/10)] = 0.971
Entropy of Pitch
Total Events for Spin = 5
P(Green) = 3/5
P(Blue) = 2/5
Entropy = -[3/5*log2(3/5) + 2/5*log2(2/5)] = 0.971
Total Events for Pace = 5
P(Green) = 1/5
P(Blue) = 4/5
Entropy = -[3/5*log2(3/5) + 2/5*log2(2/5)] = 0.721
Weighted Entropy = Probability of Events of Spin*Entropy of Spin + Probability of Events of Pace*Entropy of Pace
Weighted Entropy = (5/10)*0.971 + (5/10)*0.721 = 0.846
Information Gain = Entropy of winner – weighted entropy = 0.971 – 0.846 = 0.125
Rounded of to two decimal places = 0.12
Q10 – Given the two-dimensional dataset consisting of 5 data points from two classes (circles and squares) and assume that the Euclidean distance is used to measure the distance between two points. The minimum odd value of 𝑘 in 𝑘-nearest neighbor algorithm for which the diamond (⋄) shaped data point is assigned the label square is ______.

(GATE DS&AI 2024)
Ans – (5)
Explanation – The minimum odd value of k in k-nearest neighbor.
When k = 1 (odd number), you look at the 1 closest point to the diamond. There is circle and the diamond will take the same label (circle or square) as this one nearest point.
So, diamond will be circle if k = 1.
When k = 3 (odd number), you look at the 3 closest point to the diamond. There are 2 circle and one square and the diamond will take the same label (whichever is more).
So, diamond will be circle if k = 3.
When k = 5 (odd number), you look at the 5 closest point to the diamond. There are 2 circle and 3 squares and the diamond will take the same label (whichever is more).
So, diamond will be a square if k = 5.
Hence, 5 is the answer.



