Aptitude Test Q1 to Q10
Q 1 to 5 are of 1 mark
Q 6 to 10 are of 2 marks
Q1 – If ‘→’ denotes increasing order of intensity, then the meaning of the words [dry → arid → parched] is analogous to [diet → fast → ________ ].
Which one of the given options is appropriate to fill the blank?
(A) starve
(B) reject
(C) feast
(D) Deny
Ans – (A)
Explanation – The series of words [dry→ arid→ parched] illustrates an intensification of dryness, or a descending level of moisture. While “dry” indicates having a low amount of moisture, “arid” suggests a high level of dryness, and “parched” means devoid of moisture. A similar relationship in terms of progressively more food deprivation exists with the series of words [diet → fast → ______]. Diet suggests some restriction in food intake, while fast is defined as abstaining from food for a limited time. The greatest level of food deprivation is starved. The option 1 is starve, since it suggests the highest level of food deprivation.
Q2 – If two distinct non-zero real variables 𝑥 and 𝑦 are such that (𝑥+𝑦) is proportional to (𝑥−𝑦) then the value of 𝑥/𝑦
(A) depends on 𝑥𝑦
(B) depends only on 𝑥 and not on 𝑦
(C) depends only on 𝑦 and not on 𝑥
(D) is a constant
Ans – (D)
Explanation – The condition is (x + y) is proportional to (x – y).
If you increase x and y becomes constant, then (x + y) will be directly proportional to (x – y).
If you increase y and x becomes constant, then (x + y) will be inversely proportional to (x – y).
So, if x + y = C(x – y) C is a constant
Then, x + y = Cx – Cy
So, x – Cx = -y – Cy
Common, x(1 – C) = -y(1 + C)
Now, x/y = -(1 + C)/(1 – C) = Constant
So, x/y is a constant.
Q3 – Consider the following sample of numbers:
9, 18, 11, 14, 15, 17, 10, 69, 11, 13
The median of the sample is
(A) 13.5
(B) 14
(C) 11
(D) 18.7
Ans – (A)
Explanation – When the values are sorted from lowest to highest, the median of a dataset is the number located in the middle.
It provides an interpretation of the “central” tendency of a data set. If n is odd, this will be that centre number. If n is even, the median is the average of the two centre numbers.
Sorting the given numbers – 9, 10, 11, 11, 13, 14, 15, 17, 18, 69
There are 10 numbers, so if n is even, the median is the average of the two centre numbers, 13 and 14.
So, 13.5 is the median.
Q4 – The number of coins of ₹1, ₹5, and ₹10 denominations that a person has are in the ratio 5:3:13. Of the total amount, the percentage of money in ₹5 coins is
(A) 21%
(B) 14 %
(C) 10%
(D) 30%
Ans – (C)
Explanation – The number of coins of Rs 1 = 5x * 1 = 5x
The number of coins of Rs 5 = 3x*5 = 15x
The number of coins of Rs 10 = 13x*10 = 130x
Total Rs = 150x
Of the total amount, the percentage of money in ₹5 coins is
= 15x/150x * 100 = 10%
So, option (C) is the answer.
Q5 – For positive non-zero real variables 𝑝 and 𝑞, if
log (𝑝2 +𝑞2) = log𝑝 + log𝑞 + 2log3 ,
then, the value of (𝑝4 + 𝑞4)/𝑝2𝑞2 is
(A) 79
(B) 81
(C) 9
(D) 83
Ans – (A)
Explanation – log (p2 +q2) = log p + log q + 2*log 3
- log (p2 +q2) = log pq + 2*log 3 [log p + log q = log pq]
- log (p2 +q2) = log pq + log 32 [b*log a = log ab]
- log (p2 +q2) = log pq + log 9
- log (p2 +q2) = log 9pq
- p2 + q2 = 9pq [Cancelling log]
- (p2 + q2)2 = (9pq)2
- p4 + q4 + 2p2q2 = 81p2q2
- p4 + q4 = 79p2q2
- (p4 + q4)/p2q2 = 79
Hence option (A) is the answer.
Q6 – In the given text, the blanks are numbered (i)−(iv). Select the best match for all the blanks.
Steve was advised to keep his head ____(i)___ before heading ____(ii)____ to bat; for, while he had a head ____(iii)_____ batting, he could only do so with a cool head ____(iv)_____ his shoulders.
(A) (i) down (ii) down (iii) on (iv) for
(B) (i) on (ii) down (iii) for (iv) on
(C) (i) down (ii) out (iii) for (iv) on
(D) (i) on (ii) out (iii) on (iv) for
Ans – (C)
Explanation – Steve was advised to keep his head (i) down before heading (ii) out to bat; for, while he had a head (iii) for batting, he could only do so with a cool head (iv) on his shoulders. Hence the option (C) is the answer.
In this question, you should have at least this level of English so that you can answer the question. Both English and Hindi are our official languages. But I don’t understand why there is no Hindi version of the question here.
Q7 – A rectangular paper sheet of dimensions 54 cm × 4 cm is taken. The two longer edges of the sheet are joined together to create a cylindrical tube. A cube whose surface area is equal to the area of the sheet is also taken.
Then, the ratio of the volume of the cylindrical tube to the volume of the cube is
(A) 1/π
(B) 2/π
(C) 3/π
(D) 4/π
Ans – (A)
Explanation – The rectangular paper sheet of dimension = 54 cm x 4 cm
So, area of the sheet = 54*4 = 216 cm2
For cylinder, the longer edge is joined
Height, h = 54 cm
Circumference = 4 cm = 2πr
Radius r = 2/π
Volume of the cube = πr2h = 54*2*2/π = 216/π cm3
Cube surface area = area of the sheet = 216 cm2
Cube 1 face surface area = 216/6 = 36 cm = side * side
Cube side = 6 cm
Volume of the cube = side * side * side = 216 cm3
Then, the ratio of the volume of the cylindrical tube to the volume of the cube is = 216/(π*216) = 1/π
Hence option (A) is the answer.
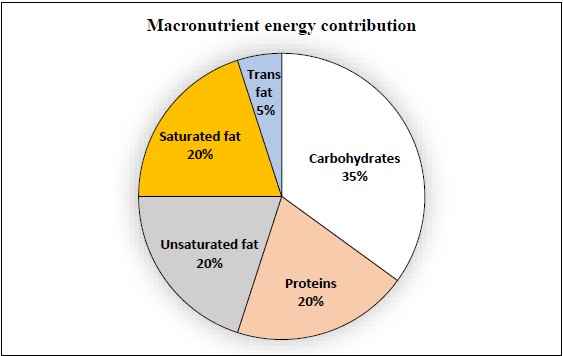
Q8 – The pie chart presents the percentage contribution of different macronutrients to a typical 2,000 kcal diet of a person.
The typical energy density (kcal/g) of these macronutrients is given in the table.
Macronutrient | Energy density (kcal/g) | |
Carbohydrates | 4 | |
Proteins | 4 | |
Unsaturated fat | 9 | |
Saturated fat | 9 | |
Trans fat | 9 |
The total fat (all three types), in grams, this person consumes is
(A) 44.4
(B) 77.8
(C) 100
(D) 3,600
Ans – (C)
Explanation – The total energy a person needs on a diet is 2000 kcal.
The macronutrients
Unsaturated fat = 20/100 * 2000 = 400 kcal
Saturated fat = 20/100 * 2000 = 400 kcal
Trans fat = 5/100 * 2000 = 100 kcal
Different micronutrients have different energy density.
So, if you need 400 kcal of Unsaturated fat, then you need 400/9 = 44.44 g of unsaturated fat.
Saturated fat = 400/9 = 44.44 g
Trans fat = 100/9 = 11.11 g
Total fats = 44.44 g + 44.44 g + 11.11 g = 99.99 g is equal to 100 g
Hence option (C) is the answer.
Q9 – A rectangular paper of 20 cm × 8 cm is folded 3 times. Each fold is made along the line of symmetry, which is perpendicular to its long edge. The perimeter of the final folded sheet (in cm) is
(A) 18
(B) 24
(C) 20
(D) 21
Ans – (A)
Explanation – The rectangular paper has dimensions = 20 cm * 8 cm
After one-fold = 10 cm * 8 cm
After second-fold = 5 cm * 8 cm
After third-fold = 5 cm * 4 cm
Then the perimeter is 5*2 + 4*2 = 18 cm
Hence the option (A) is the answer.
Q10 – The least number of squares to be added in the figure to make AB a line of symmetry is
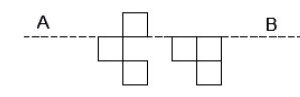
(A) 6
(B) 4
(C) 5
(D) 7
Ans – (A)
Explanation – 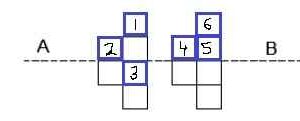
Subject Specific – Computer Science
Q11 to 35 are of 1 mark
Q11 – Let 𝑓:ℝ → ℝ be a function such that 𝑓(𝑥) = max{𝑥, 𝑥3}, 𝑥∈ℝ , where ℝ is the set of all real numbers. The set of all points where 𝑓(𝑥) is NOT differentiable is
(A) {−1,1,2}
(B) {−2,−1,1}
(C) {0,1}
(D) {−1,0,1}
Ans – (D)
Explanation – Function f(x) = max{x, x3}
The points where it is not differentiable is that, the function is not continuous at those points.
If x is max, then x ≥ x3
So, x – x3 ≥ 0
ð x(1 – x2) ≥ 0
ð x = 0 | 1 – x2 = 0
ð x = 0 | x2 = 1
ð x = 0 | x = 1 | x = -1
If x3 is max, then x3 ≥ x
So, x3 – x ≥ 0
ð x(x2 – 1) ≥ 0
ð x = 0 | x2 = 1
ð x = 0 | x = -1 | x = 1
To check whether it is differentiable or not, we can compute the derivative
F(x) = { x3, if x ≥ 1 So, F’(x) = 3x2
F(x) = ( x, if 0 ≤ x < 1 So, F’(x) = 1
F(x) = { x3, if -1 ≤ x < 0 So, F’(x) = 3x2
F(x) = { x, if -1 < x So, F’(x) = 1
Means the point where x = -1, 0 and 1, the function is not continuous. Hence option (D) is the answer.
Q12 – The product of all eigenvalues of the matrix is
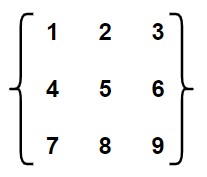
(A) −1
(B) 0
(C) 1
(D) 2
Ans – (B)
Explanation – An eigenvalue is a special number related to a square matrix that provides insight into the geometry of a square matrix. If you are given an n×n matrix A, any eigenvalue λ can be found based on the characteristic equation. det(A − λI) = 0.
Matrix = 1(5*9 – 6*8) – 2(4*9 – 6*7) + 3(4*8 – 5*7)
Matrix = -3 – 2(-6) + 3(-3) = -3 + 12 – 9 = 0
Considering the determinant of the matrix you submitted, it is 0 because one of the eigenvalues is equal to zero, consequently it indicates that the product of each eigenvalue is also equal to zero. Therefore, the correct response to your question is (B) = 0.
Q13 – Consider a system that uses 5 bits for representing signed integers in 2’s complement format. In this system, two integers 𝐴 and 𝐵 are represented as 𝐴=01010 and 𝐵=11010. Which one of the following operations will result in either an arithmetic overflow or an arithmetic underflow?
(A) 𝐴+𝐵
(B) 𝐴−𝐵
(C) 𝐵−𝐴
(D) 2∗𝐵
Ans – (B)
Explanation – In a 5-bit two’s complement numbers can range from -16 to 15 where the leftmost bit is the sign bit (0 means positive, 1 means negative).
Given the two numbers: A = 01010 and B = 11010, we want to first convert these to decimal.
Since A starts with a 0, it is positive, and therefore its decimal number is 10, then for B which starts with a 1 (indicating a negative number), we will convert it to 2’s complement.
To do this, we will invert the bits (1’s complement) and then add 1, therefore, B = -6 after conversion.
Now, we will evaluate whether each operation has an arithmetic overflow or underflow. The option (A) addition of A + B = 10 + (-6) = 4, which is within range (-16 to 15), therefore will not cause overflow.
The option (B), subtraction A – B = 10 – (-6) = 16, is NOT within range and exceeds the maximum representable value (15) in 5-bit two’s complement, thus it will cause an overflow.
The subtraction B – A = -6 – 10 = -16, is NOT an underflow because -16 is within range.
The multiplication B x 2 = 2 x (-6) = -12, is also valid. Therefore, only A – B caused an overflow, thus the correct answer is (B).
Q14 – Consider a permutation sampled uniformly at random from the set of all permutations of {1, 2, 3, ⋯, 𝑛} for some 𝑛 ≥ 4. Let 𝑋 be the event that 1 occurs before 2 in the permutation, and 𝑌 the event that 3 occurs before 4. Which one of the following statements is TRUE?
(A) The events 𝑋 and 𝑌 are mutually exclusive
(B) The events 𝑋 and 𝑌 are independent
(C) Either event 𝑋 or 𝑌 must occur
(D) Event 𝑋 is more likely than event 𝑌
Ans – (B)
Explanation – 𝑋 be the event that 1 occurs before 2, and
𝑌 the event that 3 occurs before 4.
The X and Y are not relating to each other.
Probability of X event (1 appear before 2) = ½
Probability of Y event (3 appear before 4) = ½
Checking the Provided Options
(A) The events X and Y are mutually exclusive → False
For two events to be mutually exclusive, they cannot occur at the same time. But, both of these could occur at the same time, as seen in the permutation 1,3,2,4,5,…., so these two could not be mutually exclusive.
(B) The events X and Y are independent → True
We have proved this from a mathematical standpoint, therefore this answer is true.
(C) Either event X or event Y must occur → False
This could be exemplified by the permutation 2,1,4,3,5,… where both events X and Y do not occur. Thus this would be false.
(D) Event X is more likely than event Y → False
Both event X and event Y have the same probability; therefore, this statement would not hold true.
Q15 – Which one of the following statements is FALSE?
(A) In the cycle stealing mode of DMA, one word of data is transferred between an I/O device and main memory in a stolen cycle
(B) For bulk data transfer, the burst mode of DMA has a higher throughput than the cycle stealing mode
(C) Programmed I/O mechanism has a better CPU utilization than the interrupt driven I/O mechanism
(D) The CPU can start executing an interrupt service routine faster with vectored interrupts than with non-vectored interrupts
Ans – (C)
Explanation – Option A – In cycle stealing mode of Direct Memory Access (DMA), the DMA controller momentarily gains control over the system bus to transfer a word of data, one word at a time, between an I/O device and main memory. Since it is performing the transfer of one word at a time, we say that this statement is true.
Option B – Burst Mode DMA allows the continuous transfer of data without CPU intervention, resulting in improved throughput. Cycle Stealing DMA, on the other hand, transfers one word at a time, which is slower than burst mode. Since the throughput in burst streaming is improved compared to cycle stealing, we can say that the statement is true.
Option C – Programmed I/O requires the CPU to actively wait (polling) for the I/O operation to finish. Interrupt-driven I/O does not require the CPU to wait inactively, allowing it to continue executing instructions until the device interrupts the CPU when it is ready. Since interrupt-driven I/O leads to better CPU utilization than programmed I/O, we can conclude the statement is false.
Option D – Vectored Interrupts provide the address for Interrupt Service Routines (ISRs) directly, allowing the CPU to minimize delay caused to begin execution of the interrupt. Non-vectored Interrupts may require the CPU to poll or read the ISR address before it starts its execution, adding additional delay to the handling of the interrupt. Since vectored interrupts allow faster ISR execution, this statement is true.
Q16 – A user starts browsing a webpage hosted at a remote server. The browser opens a single TCP connection to fetch the entire webpage from the server. The webpage consists of a top-level index page with multiple embedded image objects. Assume that all caches (e.g., DNS cache, browser cache) are all initially empty.
The following packets leave the user’s computer in some order.
(i) HTTP GET request for the index page
(ii) DNS request to resolve the web server’s name to its IP address
(iii) HTTP GET request for an image object
(iv) TCP SYN to open a connection to the web server
Which one of the following is the CORRECT chronological order (earliest in time to latest) of the packets leaving the computer ?
(A) (iv), (ii), (iii), (i)
(B) (ii), (iv), (iii), (i)
(C) (ii), (iv), (i), (iii)
(D) (iv), (ii), (i), (iii)
Ans – (C)
Explanation – The sequence of steps that a user goes through when he or she loads a web page on a remote server is similar to the following. All caches (e.g., the DNS cache and the browser cache) start out empty. Therefore, the first step is to resolve the domain name of the web server to an IP address. That is done by sending a DNS request (step ii).
Once the IP address has been resolved, the next step is to establish a connection with the web server using TCP (step iv). In order to establish that connection, the user’s device sends a TCP SYN packet for the three-way handshake.
Upon completion of the TCP process, the browser sends an HTTP GET request for the index page of the web site (step i).
Then, after the browser receives the index page, it looks at the page to find other objects, like images, which it will then send the HTTP GET requests again for the images (step iii).
Q17 – Given an integer array of size N, we want to check if the array is sorted (in either ascending or descending order). An algorithm solves this problem by making a single pass through the array and comparing each element of the array only with its adjacent elements.
The worst-case time complexity of this algorithm is
(A) both Ο(𝑁) and Ω(𝑁)
(B) Ο(𝑁) but not Ω(𝑁)
(C) Ω(𝑁) but not Ο(𝑁)
(D) neither Ο(𝑁) nor Ω(𝑁)
Ans – (A)
Explanation – We are given an array of integers of size N, and we need to see whether it is sorted in ascending or descending order.
The algorithm will do this while only having to compare each element with the element next to it, in one pass through the array.
In the worst-case scenario, we will have to compare each adjacent pair to determine if the array is sorted. This means we will have to do around N−1 comparisons, or O(N). Since in the best case, or worst case, we still will need to check every element once (we can’t skip the element to compare to) when comparing adjacent elements, it is also Ω(N).
Hence, the option A is the answer.
Q18 – Consider the following C program:
#include <stdio.h>
int main(){
int a = 6;
int b = 0;
while(a < 10) {
a = a / 12 + 1;
a += b;}
printf(”%d”, a);
return 0;
}
Which one of the following statements is CORRECT?
(A) The program prints 9 as output
(B) The program prints 10 as output
(C) The program gets stuck in an infinite loop
(D) The program prints 6 as output
Ans – (C)
Explanation –
Since int a = 6 and b = 0, therefore
1st iteration
- while(a < 10) — Condition True
- a = a/12 + 1 = 6/12 + 1 = 0 + 1 [because of int]
- a += b means a gets the value of b and is increased by 1 So, a = 0 + 1 = 1
- Result is a = 1, b = 0
2nd iteration
- while(a < 10) — Condition True
- a = a/12 + 1 = 1/12 + 1 = 0 + 1 [because of int]
- a += b means a gets the value of b and is increased by 1 So, a = 0 + 1 = 1
- Result is a = 1, b = 0
Since, a is not increasing it always remains on 1 and b is 0. So, the loop will run forever.
Hence option C is the answer, the program gets stuck in an infinite loop.
Q19 – Consider the following C program:
#include <stdio.h>
void fX();
int main(){
fX();
return 0;
}
void fX(){
char a;
if((a=getchar()) != ’\n’)
fX();
if(a != ’\n’)
putchar(a);
}
Assume that the input to the program from the command line is 1234 followed by a newline character. Which one of the following statements is CORRECT?
(A) The program will not terminate
(B) The program will terminate with no output
(C) The program will terminate with 4321 as output
(D) The program will terminate with 1234 as output
Ans – (C)
Explanation – The program begins execution at the main() function, which invokes a function called fX().
Inside fX(), a character named a is read from input using getchar().
If a is not a newline character, the function invokes itself recursively to read the next character. The recursion continues until a newline character is read, at which point it stops.
The function will now start to return from the subsequent recursive calls. When the function returns from each recursive call, it checks to see if the character a is not a newline character. If it is not a newline character, it prints out that character using putchar(a). This is what causes the characters to be printed in reverse order of how they were read.
For example, if input was 1234 and was followed by a newline character, the function would read ‘1’, ‘2’, ‘3’ and then ‘4’. As the function starts to return, it prints ‘4′, then ‘3′, then ‘2’, then finally ‘1’.This is how the program ends with the output 4321. Therefore, this means the answer is (C).
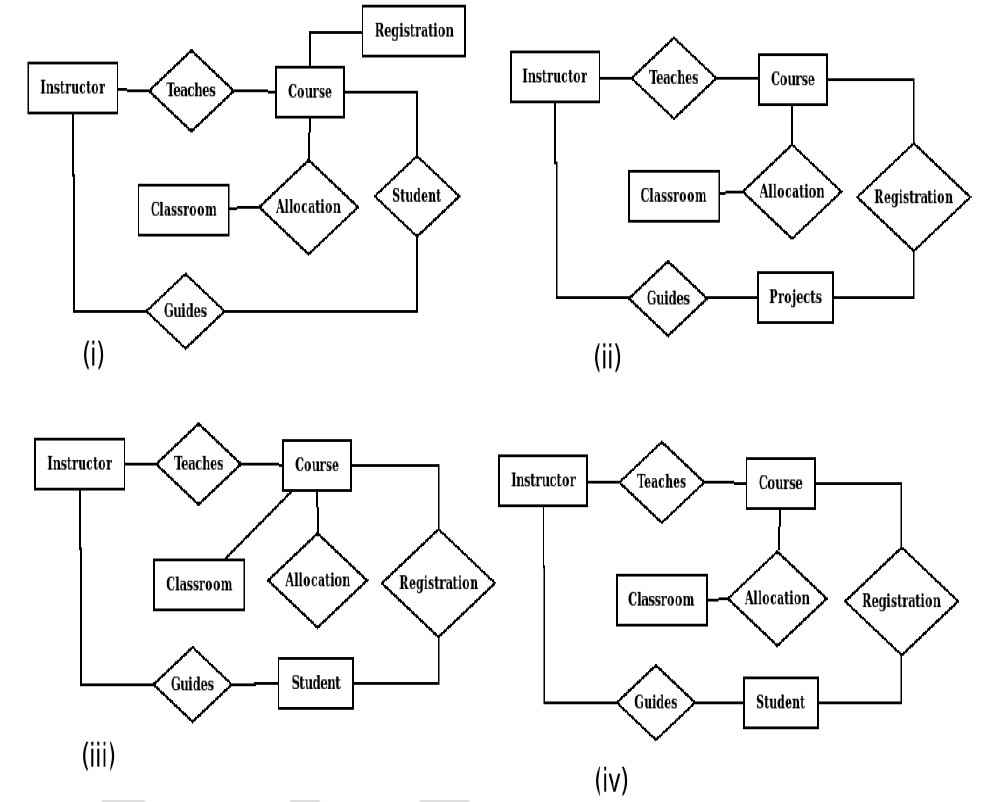
Q20 – Let S be the specification: “Instructors teach courses. Students register for courses. Courses are allocated classrooms. Instructors guide students.” Which one of the following ER diagrams CORRECTLY represents S?
 (A) (i)
(A) (i)
(B) (ii)
(C) (iii)
(D) (iv)
Ans – (D)
Explanation –
Four relationships are there
- Instructor(Rectangle) —– Teaches(diamond) —- Course(Rectangle) – Absent in None
- Student(Rectangle) —- Registers(Diamond) —- Course(Rectangle) – Absent in (i) and (ii)
- Course(Rectangle) —- Allocated(Diamond) —- Classroom(Rectangle) – Absent in (iii)
- Instructor(Rectangle) —- Guides(Diamond) —- Student(Rectangle) – Absent in (i) and (ii)
So, option D is the answer.
Q21 – In a B+ tree, the requirement of at least half-full (50%) node occupancy is relaxed for which one of the following cases?
(A) Only the root node
(B) All leaf nodes
(C) All internal nodes
(D) Only the leftmost leaf node
Ans – (A)
Explanation – The significant rule for a B+ tree is that keeps it at least 50% full (no children or half-full nodes) helps to balance the B+ tree structure and keep the search efficient. However, this rule is relaxed only for the root node.
B+ Tree Properties –
- All nodes (except for the root) must contain at least ⌈n/2⌉ children, where n is the maximum number of children a node can have.
- All data records are only stored in leaf nodes.
- The leaf nodes are linked together to facilitate range searches.
Q22 – Which of the following statements about a relation R in first normal form (1NF) is/are TRUE ?
(A) R can have a multi-attribute key
(B) R cannot have a foreign key
(C) R cannot have a composite attribute
(D) R cannot have more than one candidate key
Ans – (A, C)
Explanation – First Normal Form (1NF) requires a relation to contain only atomic (indivisible) values in each cell and have no repeating groups or arrays.
According to the rules of 1NF, a relation can have a multi-attribute key (or composite key), which means that more than one attribute can be used to identify the row uniquely. Thus, statement (A) is true.
A relation cannot have a composite attribute in 1NF because all composite attributes (e.g., a “Name” field that contains first names and last names) must be decomposed into atomic attributes. Thus, statement (C) is true as well.
However, a relation in 1NF can have a foreign key. So, both statements (B) and (D) are false because 1NF has no restrictions on the presence of foreign keys, nor does 1NF have any restrictions on having more than one candidate key. Therefore, only statements (A) and (C) are true.
Q23 – Let 𝐿1, 𝐿2 be two regular languages and 𝐿3 a language which is not regular. Which of the following statements is/are always TRUE?
(A) 𝐿1 = 𝐿2 if and only if 𝐿1∩ 𝐿2̅ =𝜙
(B) 𝐿1 ∪ 𝐿3 is not regular
(C) 𝐿3̅ is not regular
(D) 𝐿1̅ ∪ 𝐿2̅ is regular
Ans – (C, D)
Explanation – Let L1 and L2 be two regular languages, and L3 be a language that is not regular.
(A) says that L1 = L2 if and only if L1 ∩ complement of L2 = ∅. This is not always true because this would only prove one direction of set equality. To prove that L1 = L2 we must prove that L2 ∩ complement of L1 = ∅. Thus, (A) is false.
(B) says that L1 ∪ L3 is not regular. This is not always true. The union of a regular and non-regular language can be either regular or non-regular depending on the specific structure of L3. Therefore, (B) is not always true.
(C) states the complement of a non-regular language (L3) is not regular. This is always true because regular languages are closed under complementation. If the complement is regular, the original language must also be regular resulting in contradiction.
(D) states the union of the complements of two regular languages is regular. This is always true because regular languages are closed under both complement and union.
Q24 – Which of the following statements about threads is/are TRUE?
(A) Threads can only be implemented in kernel space
(B) Each thread has its own file descriptor table for open files
(C) All the threads belonging to a process share a common stack
(D) Threads belonging to a process are by default not protected from each other
Ans – (D)
Explanation –
The statement presented as (A) is incorrect. Threads may be implemented in user space and kernel space, depending on the operating system and thread library. It is, therefore, incorrect to say threads can only be implemented in kernel space.
Statement (B) is incorrect. Threads in the same process share the same file descriptor table. Thus, all threads of a process can access the same set of open files.
The statement represented as (C) is also incorrect. Threads do not share the same stack. Each thread has its own stack, this stack is used to store function calls, and local variables. However, they share the same address space, heap, and global variables.
The statement represented as (D) is true. Threads in the same process are not protected from each other by default. Because they share the same memory space, one thread can overwrite data used by another thread; this will lead to bugs if not handled properly. Therefore, the correct answer is (D).
Q25 – Which of the following process state transitions is/are NOT possible?
(A) Running to Ready
(B) Waiting to Running
(C) Ready to Waiting
(D) Running to Terminated
Ans – (B, C)
Explanation –
Option (B) Waiting to Running – It is NOT possible to transition directly between these two states. In order for a process that is in the Waiting (or blocked) state to transition to the Running state, it first has to transition to the Ready state after the event which was causing it to wait is completed, and then the scheduler has to select that process to transition to Running.
Option (C) Ready to Waiting – It is also NOT possible to transition directly between these two states. A process can only transition between Ready and Running in the Ready state, and if it needs to wait (for I/O for example) it has to transition between Running and Waiting. Therefore, a direct transition from Ready to Waiting is invalid.
Q26 – Which of the following is/are Bottom-Up Parser(s)?
(A) Shift-reduce Parser
(B) Predictive Parser
(C) LL(1) Parser
(D) LR Parser
Ans – (A, D)
Explanation – Option (A) – The Shift-Reduce Parser can be classified as a Bottom-Up Parser. The parser initiates at the input symbols and attempts to reduce it to the start symbol of the grammar. The parser will use operations of “shift” and “reduce”.
Option (B) The Predictive Parser can be classified as a Top-Down Parser. The parser predicts what rules to apply in accordance with the current input, and it works from the start symbol of the grammar to the input string itself.
Option (C) – The LL(1) Parser can be classified as a Top-Down Parser. The first “L” indicates that the parser processes the input from Left-to-right, and the second “L” indicates that the parser generates a Leftmost derivation. To make decisions, it requires 1 lookahead symbol.
Option (D) – The LR Parser can be classified as a Bottom-Up Parser. The parser processes the input Left-to-right, while producing a Rightmost derivation (in reverse). It is considered a very powerful, and popular type of a bottom-up parser.
Q27 – Let 𝐴 and 𝐵 be two events in a probability space with 𝑃(𝐴) = 0.3, 𝑃(𝐵) = 0.5, and 𝑃(𝐴∩𝐵) = 0.1. Which of the following statements is/are TRUE?
(A) The two events 𝐴 and 𝐵 are independent
(B) 𝑃(𝐴 ∪ 𝐵) = 0.7
(C) 𝑃(𝐴 ∩ 𝐵C ) = 0.2, where 𝐵C is the complement of the event 𝐵
(D) 𝑃(𝐴C ∩ 𝐵C) = 0.4, where 𝐴C and 𝐵C are the complements of the events 𝐴 and 𝐵, respectively
Ans – (B, C)
Explanation –
We have the probabilities of two events, P(A)=0.3, P(B)=0.5, and the intersection P(A∩B)=0.1.
Option (A), for A and B to be independent, we must have P(A∩B) = P(A) ⋅ P(B). However, 0.3 ⋅ 0.5 = 0.15 is not equal to the provided P(A∩B) of 0.1. Therefore, A and B are not independent, and so (A) is false.
Option (B), if the union A ∪ B is equal to 0.7. We calculate the union using the formula P(A∪B) = P(A) + P(B) − P(A∩B) which gives us P(A∪B) = 0.3 + 0.5 − 0.1 = 0.7 which means (B) is true.
Next, let’s consider option (C) which describes P(A∩BC ) = 0.2. This means the probability that A occurs but B does not. To calculate this, we can use P(A) − P(A∩B), which allows us to find P(A∩BC) = 0.3 − 0.1 = 0.2, therefore (C) is true.
Finally, let’s examine the last option (D) which refers to the event AC∩BC = 0.4 which is the probability that neither A occurs nor B. This is equal to 1 − P(A∪B), which is equal to 1 − 0.7 = 0.3. Therefore, D is false.
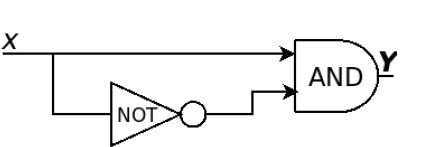
Q28 – Consider the circuit shown below where the gates may have propagation delays. Assume that all signal transitions occur instantaneously and that wires have no delays. Which of the following statements about the circuit is/are CORRECT?

(A) With no propagation delays, the output 𝒀 is always logic Zero
(B) With no propagation delays, the output 𝒀 is always logic One
(C) With propagation delays, the output 𝒀 can have a transient logic One after 𝑿 transitions from logic Zero to logic One
(D) With propagation delays, the output 𝒀 can have a transient logic Zero after 𝑿 transitions from logic One to logic Zero
Ans – (A, C)
Explanation – The output Y is represented by the expression Y = X⋅X’
The expression always evaluates to 0 because anything AND its complement will always be zero.
In the case with no propagation delays
The NOT gate will give the complement of X immediately, then the AND gate computes X⋅X’, which will yield 0.
Thus, option A is correct.
In the case with propagation delays
In a real circuit, there may be a small and finite time for a gate to respond out to its output. If you were to make X transition from 0 to 1, the inverter (the NOT gate) may not transition to 0 at exactly the same time. At that moment (very short), both inputs to the AND gate are both 1, in this case there will be an output Y of 1, which may eventually will settle to 0. A transient output Y as we see occurs with a glitch.
Meaning the output somehow happened for a very short moment, as you would blink rather quickly, thus, option C is correct.
Q29 – TCP client P successfully establishes a connection to TCP server Q. Let 𝑁P denote the sequence number in the SYN sent from P to Q. Let 𝑁Q denote the acknowledgement number in the SYN ACK from Q to P. Which of the following statements is/are CORRECT?
(A) The sequence number 𝑁P is chosen randomly by P
(B) The sequence number 𝑁P is always 0 for a new connection
(C) The acknowledgement number 𝑁Q is equal to 𝑁p
(D) The acknowledgement number 𝑁Q is equal to 𝑁P + 1
Ans – (A, D)
Explanation – To establish a TCP connection, the client and server must first perform a three-way handshake.
In the first stage of the handshake, the client (P) initiates the connection with the server (Q) by sending a SYN message to the server with a sequence number of 𝑁p.
Like any sequence number, this sequence number is always random, which adds a slight security aspect and helps mitigate certain attack types. Therefore, option (A) is correct.
The sequence number 𝑁P is always 0 for a new connection is false, so option (B) is incorrect.
After the server receives the SYN from the client, it sends a SYN-ACK response to the client. In this response, the server includes its own randomly generated sequence number and an acknowledgment number 𝑁Q, which acknowledges receipt of the client’s SYN. The acknowledgment number 𝑁Q is equal to 𝑁p + 1, meaning that the server is ready to receive the next byte. Therefore, option (C) must be incorrect, and option (D) must be correct.
Q30 – Consider a 5-stage pipelined processor with Instruction Fetch (IF), Instruction Decode (ID), Execute (EX), Memory Access (MEM), and Register Writeback (WB) stages. Which of the following statements about forwarding is/are CORRECT?
(A) In a pipelined execution, forwarding means the result from a source stage of an earlier instruction is passed on to the destination stage of a later instruction
(B) In forwarding, data from the output of the MEM stage can be passed on to the input of the EX stage of the next instruction
(C) Forwarding cannot prevent all pipeline stalls
(D) Forwarding does not require any extra hardware to retrieve the data from the pipeline stages
Ans – (A, B, C)
Explanation – In a 5-stage pipelined CPU consisting of front-end stages (IF & ID) and back-end stages (EX, MEM, WB), forwarding can mitigate pipeline stalls by allowing the processor to route data directly from one pipeline stage to another without going through every pipeline stage. Hence, option (A) is true.
Option (B) is also true, as a common scenario for forwarding is forwarding the output of the MEM stage of one instruction to the EX-stage of another instruction if the data is required. Option (C) is true in acknowledging that forwarding does help reduce data hazards to avoid stalls in many circumstances, however, forwarding is unable to resolve every situation, particularly with load-use hazards in the situation where the data is still being generated in the previous load instruction, and have not yet been fetched into the register.
Option (D) is false. Forwarding that helps to minimize stalls does come at the cost of extra hardware for multiplexers and forwarding logic and does add some extra functionality to detect the hazards a route data from pipeline stage to pipeline stage. The correct answer is, therefore, A, B, and C.
Q31 – Which of the following fields is/are modified in the IP header of a packet going out of a network address translation (NAT) device from an internal network to an external network?
(A) Source IP
(B) Destination IP
(C) Header Checksum
(D) Total Length
Ans – (A, C)
Explanation – When a packet travels out of a Network Address Translation (NAT) device from an internal network to an external network, some fields in the IP header are changed to give the appropriate routing and response handling.
Option (A) – The Source IP is modified by the NAT device. The NAT device modifies the internal private IP address (i.e. 192.168.x.x.) to the public IP address of the NAT device so that the response from the external server is routed back correctly. This is true.
Option (B) – The Destination IP would not require any modification as the packet is still being sent to the same external server. The NAT device does not need to modify this field. This is false.
Option (C) – The Header Checksum would logically be modified. Since the IP header was modified (because of the new source IP), the header checksum will need recalculation. This is true.
Option (D) – The Total Length would not be modified as the NAT process has not changed the size of the IP packet. This is false.
Q32 – Let 𝐴 and 𝐵 be non-empty finite sets such that there exist one-to-one and onto functions (i) from 𝐴 to 𝐵 and (ii) from 𝐴 × 𝐴 to 𝐴 ∪ 𝐵. The number of possible values of |𝐴| is __________
Ans – (2)
Explanation – Let ∣A∣ = n, and there exists a bijection (one-to-one and onto function) from A → B. So, ∣A∣ = ∣B∣ and ∣B∣ = n
Also, ∣A × A∣ = n × n = n2
And, ∣A ∪ B∣ ≤ 2n|
From the bijection A × A → A ∪ B,
we get n2 ≤ 2n
- n (n−2) ≤ 0
- n = 0 this is not right as A and B are non-empty sets
- n = 2, this is correct.
So, the number of possible values of |𝐴| is 2.
Q33 – Consider the operator precedence and associativity rules for the integer arithmetic operators given in the table below.  The value of the expression 3+1+5∗2/7+2−4−7−6/2 as per the above rules is __________
The value of the expression 3+1+5∗2/7+2−4−7−6/2 as per the above rules is __________
Ans – (6)
Explanation – We take the highest precedence first, and put the parentheses with the associativity.
- 3+1+5∗2 / 7+2−4−7−6 / 2
- ((3 + 1) + 5) * 2 / (7 + 2) – 4 – 7 – 6 / 2 [ + has highest precedence]
- ((3 + 1) + 5) * 2 / ((7 + 2) – (4 – (7 – 6))) / 2 [ – has high precedence]
- (((3 + 1) + 5) * 2) / ((7 + 2) – (4 – (7 – 6))) / 2 [ * has medium precedence]
- ((((3 + 1) + 5) * 2) / (((7 + 2) – (4 – (7 – 6))) / 2)) [ / has low precedence]
- (((4 + 5) * 2) / ((9 – (4 – (7 – 6))) / 2))
- ((9 * 2) / ((9 – ( 4 – 1)) / 2))
- (18 / ((9 – 3) / 2))
- (18 / (6 / 2))
- (18 / 3) = 6 Ans.
Q34 – The number of spanning trees in a complete graph of 4 vertices labelled A, B, C, and D is _________.
Ans – (16)
Explanation – To find the number of spanning trees in a complete graph with n vertices, we use Cayley’s formula.
For a complete graph with n vertices, the number of spanning trees is nn-2.
For n = 4, the number of spanning trees is 44-2 = 16.
Q35 – Consider the following two relations, R(A,B) and S(A,C):
R S
A B A C
10 20 10 90
20 30 30 45
30 40 40 80
30 50
50 95
The total number of tuples obtained by evaluating the following expression 𝝈𝑩<𝑪 (𝑹⋈𝑹.𝑨=𝑺.𝑨 𝑺) is _________.
Ans – (2)
Explanation –
Perform a natural join on R.A = S.A
R | S | ||
A | B | A | C |
10 | 20 | 10 | 90 |
30 | 40 | 30 | 45 |
30 | 50 | 30 | 45 |
Apply Condition B < C
R | S | ||
A | B | A | C |
10 | 20 | 10 | 90 |
30 | 40 | 30 | 45 |
The total number of tuples obtained by evaluating the following expression 𝝈𝑩<𝑪 (𝑹⋈𝑹.𝑨=𝑺.𝑨 𝑺) is 2.
Q36 – 65 are of 2 marks
Q36 – Consider a network path P—Q—R between nodes P and R via router Q. Node P sends a file of size 106 bytes to R via this path by splitting the file into chunks of 103 bytes each. Node P sends these chunks one after the other without any wait time between the successive chunk transmissions.
Assume that the size of extra headers added to these chunks is negligible, and that the chunk size is less than the MTU.
Each of the links P—Q and Q—R has a bandwidth of 106 bits/sec, and negligible propagation latency. Router Q immediately transmits every packet it receives from P to R, with negligible processing and queueing delays. Router Q can simultaneously receive on link P—Q and transmit on link Q—R.
Assume P starts transmitting the chunks at time 𝑡 = 0.
Which one of the following options gives the time (in seconds, rounded off to 3 decimal places) at which R receives all the chunks of the file?
(A) 8.000
(B) 8.008
(C) 15.992
(D) 16.000
Ans – (B)
Explanation – A file size of 10⁶ bytes is transmitted from node P to a node R through router Q. The file is broken into chunks of size 10³ bytes and therefore, there are 1000 chunks. Chunks are of size 8000 bits.
The bandwidth of the links P–Q and Q–R are both 10⁶ bits/sec, and there are no propagation, processing, or queuing delays. Router Q, can receive and transmit packets at the same time. This means that when P sends, it does so continuously, with no idle time, and it takes 8000 bits/106 bits/sec = 0.008 sec.
Since Q can immediately pass each chunk onto the next chunk, the first chunk arrives after 0.008 seconds.
The transmitting of the chunks follows the pipelining nature, and because router Q also forwards at the same time, every subsequent chunk will reach R after an additional 0.008 seconds. The last chunk, the 1000th chunk, begins transmitting from P at 7.992 seconds and finishes transmitting at 8.000 seconds. It is forwarded by Q immediately and reaches R at 8.008 seconds. Therefore, R received its last chunk of the file at 8.008 seconds.
Q37 – Consider the following syntax-directed definition (SDD).
𝑆→𝐷𝐻𝑇𝑈 | { 𝑆.𝑣𝑎𝑙 = 𝐷.𝑣𝑎𝑙 + 𝐻.𝑣𝑎𝑙 + 𝑇.𝑣𝑎𝑙 + 𝑈.𝑣𝑎𝑙; } |
𝐷→”M”𝐷1 | { 𝐷.𝑣𝑎𝑙 = 5 + 𝐷1.𝑣𝑎𝑙; } |
𝐷→𝜖 | { 𝐷.𝑣𝑎𝑙 = −5; } |
𝐻→”L”𝐻1 | { 𝐻.𝑣𝑎𝑙 = 5∗10 + 𝐻1.𝑣𝑎𝑙; } |
𝐻→𝜖 | { 𝐻.𝑣𝑎𝑙 = −10; } |
𝑇→”C”𝑇1 | { 𝑇.𝑣𝑎𝑙 = 5∗100 + 𝑇1.𝑣𝑎𝑙; } |
𝑇→𝜖 | { 𝑇.𝑣𝑎𝑙 = −5; } |
𝑈→”K” | { 𝑈.𝑣𝑎𝑙 = 5; } |
Given “MMLK” as the input, which one of the following options is the CORRECT value computed by the SDD (in the attribute 𝑆.𝑣𝑎𝑙)?
(A) 45
(B) 50
(C) 55
(D) 65
Ans – (A)
Explanation – This question wants you to calculate a value computed by the SDD. Input “MMLK” is given and the gramma is given.
To determine S, we need to separate “MMLK” into 4 parts.
D – something beginning with M
D -> “M” D1 -> Adds 5 each time
D -> 𝜖 -> -5 from the value
Input has 2 times M. So, +5 +5 -5 = 5
H – something beginning with L
H -> “L” H1 -> Adds 5*10 each time
H -> 𝜖 -> -10 from the value
Input has next alphabet L. So, 5*10 – 10 = 40.
T – something beginning with C
T -> “C” T1 -> Adds 5*100 each time
T -> 𝜖 -> -5 from the value
There is no C in the input. So, -5 because of no C.
U – the final letter K
U -> “K” -> Adds 5 each time
Input has next alphabet K. So, 5 because of 1 K.
Total value = 𝑆.𝑣𝑎𝑙 = 𝐷.𝑣𝑎𝑙 + 𝐻.𝑣𝑎𝑙 + 𝑇.𝑣𝑎𝑙 + 𝑈.𝑣𝑎𝑙;
Total value = 𝑆.𝑣𝑎𝑙 = 5 + 40 – 5 + 5 = 45.
Hence, option (A) is the answer.
Q38 – Consider the following grammar 𝐺, with 𝑆 as the start symbol. The grammar 𝐺 has three incomplete productions denoted by (1), (2), and (3).
𝑆 → 𝑑𝑎𝑇 | (1)
𝑇 → 𝑎𝑆 | 𝑏𝑇 | (2)
𝑅 → (3) | 𝜖
The set of terminals is {𝑎, 𝑏, 𝑐, 𝑑, 𝑓}. The FIRST and FOLLOW sets of the different non-terminals are as follows.
FIRST(𝑆) = {𝑐, 𝑑, 𝑓}, FIRST(𝑇) = {𝑎, 𝑏, 𝜖}, FIRST(𝑅) = {𝑐, 𝜖}
FOLLOW(𝑆) = FOLLOW(𝑇) = {𝑐, 𝑓, $}, FOLLOW(𝑅) = {𝑓}
Which one of the following options CORRECTLY fills in the incomplete productions?
(A) (1) 𝑆→𝑅𝑓 (2) 𝑇→𝜖 (3) 𝑅→𝑐𝑇𝑅
(B) (1) 𝑆→𝑓𝑅 (2) 𝑇→𝜖 (3) 𝑅→𝑐𝑇𝑅
(C) (1) 𝑆→𝑓𝑅 (2) 𝑇→𝑐𝑇 (3) 𝑅→𝑐𝑅
(D) (1) 𝑆→𝑅𝑓 (2) 𝑇→𝑐𝑇 (3) 𝑅→𝑐𝑅
Ans – (A)
Explanation –
Terminals: {a, b, c, d, f}
FIRST(S) = {c, d, f}
FIRST(T) = {a, b, ε}
FIRST(R) = {c, ε}
FOLLOW(S) = FOLLOW(T) = {c, f, $}
FOLLOW(R) = {f}
S → daT | (1)
T → aS | bT | (2)
R → (3) | ε
In Option A and D, S → Rf
If R → cTR | ε, then FIRST(R) = {c, ε}
So FIRST(S) = {c, d, f}
In Option B and C, S → fR
Then FIRST(S) starts with f, but now how will c be in FIRST(S)?
So, our assumption is correct. The answer is option (A) or (D).
In Option A, 𝑇 → 𝜖
If T → aS | bT | ε, then FIRST(T) = {a, b, ε}
In Option D, 𝑇 → 𝑐𝑇
If T → aS | bT | 𝑐𝑇, then FIRST(T) = {a, b, c} which is wrong.
So, our assumption is correct. The answer is option (A).
Q39 – Consider the following pseudo-code.
𝐿1: 𝑡1= −1
𝐿2: 𝑡2 = 0
𝐿3: 𝑡3 = 0
𝐿4: 𝑡4 = 4∗𝑡3
𝐿5: 𝑡5 = 4∗𝑡2
𝐿6: 𝑡6 = 𝑡5∗𝑀
𝐿7: 𝑡7 = 𝑡4+𝑡6
𝐿8: 𝑡8 = 𝑎[𝑡7]
𝐿9: if 𝑡8 <= 𝑚𝑎𝑥 goto 𝐿11
𝐿10: 𝑡1 = 𝑡8
𝐿11: 𝑡3 = 𝑡3+1
𝐿12: if 𝑡3 < 𝑀 goto 𝐿4
𝐿13: 𝑡2 = 𝑡2+1
𝐿14: if 𝑡2 < 𝑁 goto 𝐿3
𝐿15: 𝑚𝑎𝑥 = 𝑡1
Which one of the following options CORRECTLY specifies the number of basic blocks and the number of instructions in the largest basic block, respectively ?
(A) 6 and 6
(B) 6 and 7
(C) 7 and 7
(D) 7 and 6
Ans – (D)
Explanation –
A basic block is defined as a series of instructions that
- Execute sequentially with no jumps or branches in between.
- It must start execution only when control comes from outside the block (one instruction is executed after another).
- Execution of a basic block ends when either:
A jump, goto, or if statement occurs,
Or the next instruction is branch target.
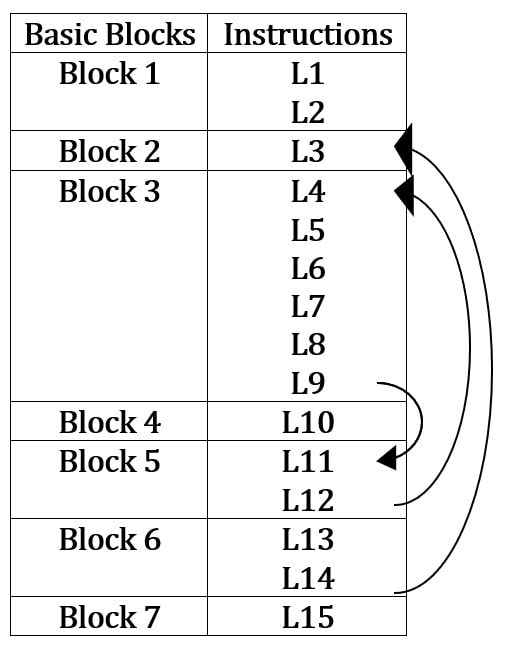
There are 7 blocks and the largest block 3 has 6 instructions.
Q40 – Consider the following two threads T1 and T2 that update two shared variables a and b. Assume that initially a = b = 1.
Though context switching between threads can happen at any time, each statement of T1 or T2 is executed atomically without interruption.
T1
a = a + 1;
b = b + 1;
T2
b = 2 * b;
a = 2 * a;
Which one of the following options lists all the possible combinations of values of a and b after both T1 and T2 finish execution?
(A) (a = 4, b = 4); (a = 3, b = 3); (a = 4, b = 3)
(B) (a = 3, b = 4); (a = 4, b = 3); (a = 3, b = 3)
(C) (a = 4, b = 4); (a = 4, b = 3); (a = 3, b = 4)
(D) (a = 2, b = 2); (a = 2, b = 3); (a = 3, b = 4)
Ans – (A)
Explanation –
There are 6 orders in which T1 and T2 finishes execution.
Initially a = 1, b = 1
1. T1 full finish, T2 full finish
a = a + 1 (a = 2)
b = b + 1 (b = 2)
b = 2 * b (b = 4)
a = 2 * a (a = 4)
(a = 4, b = 4)
.
2. T2 full finish, T1 full finish
b = 2 * b (b = 2)
a = 2 * a (a = 2)
a = a + 1 (a = 3)
b = b + 1 (b = 3)
(a = 3, b = 3)
.
3. T1 1st instr, T2 1st instr, T1 2nd instr, T2 2nd instr
a = a + 1 (a = 2)
b = 2 * b (b = 2)
b = b + 1 (b = 3)
a = 2 * a (a = 4)
(a = 4, b = 3)
.
4. T2 1st instr, T1 1st instr, T2 2nd instr, T1 2nd instr
b = 2 * b (b = 2)
a = a + 1 (a = 2)
a = 2 * a (a = 4)
b = b + 1 (b = 3)
(a = 4, b = 3)
.
5. T1 1st instr, T2 full finish, T1 2nd instr
a = a + 1 (a = 2)
b = 2 * b (b = 2)
a = 2 * a (a = 4)
b = b + 1 (b = 3)
(a = 4, b = 3)
.
6. T2 1st instr, T1 full finish, T2 2nd instr
b = 2 * b (b = 2)
a = a + 1 (a = 2)
b = b + 1 (b = 3)
a = 2 * a (a = 3)
(a = 3, b = 3)
Option (A) is the answer.
Q41 – An array [82, 101, 90, 11, 111, 75, 33, 131, 44, 93] is heapified. Which one of the following options represents the first three elements in the heapified array?
(A) 82, 90, 101
(B) 82, 11, 93
(C) 131, 11, 93
(D) 131, 111, 90
Ans – (D)
Explanation – Heapifying an array is the act of transforming an array into a heap data type (either a max- or min-heap).
In a given max-heap, for each parent node, the value of each parent node is greater than or equal to the value of each of its children. The last non-leaf node is computed from the last element in the array, moving up toward element one in the array. Processing each parent node upward fixes the heap property of the nodes held to ensure a valid heap property.

Q42 – Consider the following recurrence relation:
𝑇(𝑛) = {√𝑛𝑇(√𝑛) + 𝑛 for 𝑛≥1,
𝑇(𝑛) = {1 for 𝑛=1.
Which one of the following options is CORRECT?
(A) 𝑇(𝑛)= Θ(𝑛 loglog𝑛)
(B) 𝑇(𝑛)=Θ(𝑛 log𝑛)
(C) 𝑇(𝑛)=Θ(𝑛2 log𝑛)
(D) 𝑇(𝑛)=Θ(𝑛2 loglog𝑛)
Ans – (A)
Explanation – 
Q43 – Consider a binary min-heap containing 105 distinct elements. Let 𝑘 be the index (in the underlying array) of the maximum element stored in the heap. The number of possible values of 𝑘 is
(A) 53
(B) 52
(C) 27
(D) 1
Ans – (A)
Explanation – In this question, we are finding leaf nodes because maximum elements are stored in the leaf node as this is a min – heap.
In min-heap, the minimum element is always the root and maximum elements cover up the leaf nodes.
The leaf node in an n element heap = n – ⎣n/2⎦
= 105 – ⎣105/2⎦
= 105 – 52 = 53
Hence, number of possible values of k = 53.
Q44 – The symbol → indicates functional dependency in the context of a relational database. Which of the following options is/are TRUE?
(A) (𝑋,𝑌) → (𝑍,𝑊) implies 𝑋 → (𝑍,𝑊)
(B) (𝑋,𝑌) → (𝑍,𝑊) implies (𝑋,𝑌) → 𝑍
(C) ((𝑋,𝑌) → 𝑍 and 𝑊 → 𝑌) implies (𝑋,𝑊) → 𝑍
(D) (𝑋 → 𝑌 and 𝑌 → 𝑍) implies 𝑋 → 𝑍
Ans – (B, C, D)
Explanation –
In relational databases, a functional dependency (FD) uses the notation → to indicate that one set of attributes uniquely determines another. For example, if X → Y, it indicates that knowing the value of X is sufficient to know the value of Y.
Option (A) statement is not necessarily true because it takes the combination of both X and Y to determine Z and W. Knowing only X may not be sufficient.
Option (B) is true due to the decomposition rule of functional dependencies, because when a group of attributes determines another group of attributes, it must also determine every single attribute in that group.
Option (C) is true because through W we can determine Y, and now with X we determine Z. This follows from the properties of transitivity and augmentation of functional dependencies.
Option (D) states that if X → Y and Y → Z, then X → Z. This is a well-known transitivity rule, and it is true.
Q45 – Let 𝐺 be a directed graph and 𝑇 a depth first search (DFS) spanning tree in 𝐺 that is rooted at a vertex 𝑣. Suppose 𝑇 is also a breadth first search (BFS) tree in 𝐺, rooted at 𝑣. Which of the following statements is/are TRUE for every such graph 𝐺 and tree 𝑇 ?
(A) There are no back-edges in 𝐺 with respect to the tree 𝑇
(B) There are no cross-edges in 𝐺 with respect to the tree 𝑇
(C) There are no forward-edges in 𝐺 with respect to the tree 𝑇
(D) The only edges in 𝐺 are the edges in 𝑇
Ans – (C)
Explanation – We have given a directed graph G and a spanning tree T which was formed from both a Depth First Search (DFS) and a Breadth First Search (BFS) with respect to the same root vertex v.
In DFS, you will find edges in the directed graph G being defined as any of the following – tree edges, back edges, forward edges, or cross edges.
When a tree is a BFS-tree, the vertex is visited in what is known as levels. Thus, in one level you will find child vertices and in the next level the grandchildren, and so on. Hence, a forward edge from a parent vertex to any granddaughter vertex will violate the level structure of the BFS search, which means there could not be any forward edges with respect to tree T. Therefore, the only correct option is (C).
Q46 – Consider the following read-write schedule 𝑆 over three transactions 𝑇1, 𝑇2, and 𝑇3, where the subscripts in the schedule indicate transaction IDs:
𝑆: 𝑟1(𝑧); 𝑤1(𝑧); 𝑟2(𝑥); 𝑟3(𝑦); 𝑤3(𝑦); 𝑟2(𝑦); 𝑤2(𝑥); 𝑤2(𝑦);
Which of the following transaction schedules is/are conflict equivalent to 𝑆 ?
(A) 𝑇1 𝑇2 𝑇3
(B) 𝑇1 𝑇3 𝑇2
(C) 𝑇3 𝑇2 𝑇1
(D) 𝑇3 𝑇1 𝑇2
Ans – (B, C, D)
Explanation – To find out which transaction schedules are conflict equivalent to schedule 𝑆, which maintains the ordering of the conflicting operations between transactions.
The schedule 𝑆 is: r₁(z); w₁(z); r₂(x); r₃(y); w₃(y); r₂(y); w₂(x); w₂(y).
In schedule 𝑆, when two operations from different transactions access a data item and at least one of them is a write, the two operations are in conflict.
The key conflicts are w₃(y) from transaction T3 precedes r₂(y) and w₂(y) from transaction T2, meaning that T3 must precede T2 in any conflict equivalent schedule. T1 accesses only z, meaning it does not conflict with T2 or T3. Therefore, it can appear anywhere.
Option (A), T1 T2 T3 is not conflict equivalent because T3 is after T2, and the ordering for the conflicts is not present.
Option (B), T1 T3 T2 does keep all of the ordering of the conflicts.
Option (C), T3 T2 T1 supports the conflict between T3 and T2 in addition to T3. Where T1 can appear anywhere. Finally,
Option (D), T3 T1 T2, also keeps T3 preceding T2, and T1 can also appear anywhere.
Q47 – Consider a Boolean expression given by 𝐹(𝑋,𝑌,𝑍)=Σ(3,5,6,7)
Which of the following statements is/are CORRECT?
(A) 𝐹(𝑋,𝑌,𝑍) = Π(0,1,2,4)
(B) 𝐹(𝑋,𝑌,𝑍) = 𝑋𝑌+𝑌𝑍+𝑋𝑍
(C) 𝐹(𝑋,𝑌,𝑍) is independent of input 𝑌
(D) 𝐹(𝑋,𝑌,𝑍) is independent of input 𝑋
Ans – (A, B)
Explanation –

F(X, Y, Z) = XY + YZ + XZ. Hence option (B) is correct.
F(X, Y, Z) = Σ(3, 5, 6, 7). This indicates that the function is a 1 for the min-terms 3,5,6,7. The min-terms not in F are 0, 1, 2, and 4. This means those are maxterms. So, the product-of-maxterms is Π(0,1,2,4) which is the correct dual representation. So, option (A) is correct.
Q48 – Consider the following C function definition.
int f(int x, int y) {
for (int i=0; i<y; i++) {
x = x+x+y;
}
return x;
}
Which of the following statements is/are TRUE about the above function?
(A) If the inputs are x=20, y=10, then the return value is greater than 220
(B) If the inputs are x=20, y=20, then the return value is greater than 220
(C) If the inputs are x=20, y=10, then the return value is less than 210
(D) If the inputs are x=10, y=20, then the return value is greater than 220
Ans – (B, D)
Explanation – x₁ = 2x₀ + y
x₂ = 2x₁ + y = 2(2x₀ + y) + y = 4x₀ + 3y
x₃ = 2x₂ + y = 8x₀ + 7y
So, we can say that
xₙ = 2ⁿ * x + (2ⁿ – 1) * y
Option (A) – 210*20 + (210-1)*10 = 20480 + 10230 = 30710
But 30710 is not greater than 220. Hence, its incorrect.
Option(B) – 220*20 + (220-1)*20
It is clearly seen that the result is greater than 220.
Option (C) – 210*20 + (210-1)*10 = 20480 + 10230 = 30710
But 30710 is greater than 210 (1024). Hence, its incorrect.
Option (D) – 220*10 + (220-1)*20
It is clearly seen that the result is greater than 220.
So, answer is option (B, D).
Q49 – Let 𝐴 be any 𝑛 × 𝑚 matrix, where 𝑚 >𝑛. Which of the following statements is/are TRUE about the system of linear equations 𝐴𝑥=0 ?
(A) There exist at least 𝑚−𝑛 linearly independent solutions to this system
(B) There exist 𝑚−𝑛 linearly independent vectors such that every solution is a linear combination of these vectors
(C) There exists a non-zero solution in which at least 𝑚−𝑛 variables are 0
(D) There exists a solution in which at least 𝑛 variables are non-zero
Ans – (A)
Explanation – Assume that A is an n × m matrix where m > n. This implies that A has m variables (because each column corresponds to a variable in the equation Ax = 0). This means we only have n equations (because there are n rows). You have more variables than equations.
For example, you could think of 3 equations and 5 variables. Is it possible to find the solution for 5 unknowns using only 3 equations? No! Thus, at least m−n variables can be chosen freely. So, in option (A) there will be at least m−n linearly independent solutions to this system!
Q50 – Consider the 5-state DFA 𝑀 accepting the language 𝐿(𝑀) ⊂ (0+1)* shown below. For any string 𝑤∈(0+1)* let 𝑛0(𝑤) be the number of 0′𝑠 in 𝑤 and 𝑛1(𝑤) be the number of 1′𝑠 in 𝑤.

Which of the following statements is/are FALSE?
(A) States 2 and 4 are distinguishable in 𝑀
(B) States 3 and 4 are distinguishable in 𝑀
(C) States 2 and 5 are distinguishable in 𝑀
(D) Any string 𝑤 with 𝑛0(𝑤)=𝑛1(𝑤) is in 𝐿(𝑀)
Ans – (B, C)
Explanation – In order to check for distinguishability between two states, we try to be able to generate a string that starts at both states and leads to two different outcomes differentiated by one outcome leading to an accepting state and the other leading to a non-accepting state.
Option (A) – States 2 and 4 are distinguishable
For input 0 – State 2 -> State 3 (non-accepting state)
For input 0 – State 4 -> State 1 (accepting state)
For input 1 – State 2 -> State 1 (accepting state)
For input 1 – State 4 -> State 5 (non-accepting state)
This is true.
Option (B) – States 3 and 4 are distinguishable
For input 0 – State 3 -> State 1 (accepting state)
For input 0 – State 4 -> State 1 (accepting state)
For input 1 – State 3 -> State 2 (non-accepting state)
For input 1 – State 4 -> State 5 (non-accepting state)
This is False.
Option (C) – States 2 and 5 are distinguishable
For input 0 – State 2 -> State 3 (non-accepting state)
For input 0 – State 5 -> State 4 (non-accepting state)
For input 1 – State 2 -> State 1 (accepting state)
For input 1 – State 5 -> State 1 (accepting state)
This is False.
Option (D) – Any string 𝑤 with 𝑛0(𝑤)=𝑛1(𝑤) is in 𝐿(𝑀)
For input 01 – State 1 -> State 2 -> State 1
For input 0011 – State 1 -> State 2 -> State 3 -> State 2 -> State 1
For input 1100 – State 1 -> State 4 -> State 5 -> State 4 -> State 1
This is true.
Q51 – The chromatic number of a graph is the minimum number of colours used in a proper colouring of the graph. Let 𝐺 be any graph with 𝑛 vertices and chromatic number 𝑘.
Which of the following statements is/are always TRUE?
(A) 𝐺 contains a complete subgraph with 𝑘 vertices
(B) 𝐺 contains an independent set of size at least 𝑛/𝑘
(C) 𝐺 contains at least 𝑘(𝑘−1)/2 edges
(D) 𝐺 contains a vertex of degree at least 𝑘
Ans – (B, C)
Explanation – Even though a graph requires k colors to color it, it does not imply that it must have a complete subgraph k. For example, certain graphs, such as the Mycielskian graphs, have high chromatic numbers, but do not have large complete subgraphs. So, option A is not necessarily true.
In any proper coloring with k colors, the vertices are divided into k color classes. Each color class is an independent set. By the pigeonhole principle, at least one of the color classes must have size ≥⌈n/k⌉, thus at least n/k. So, option B is necessarily true.
The minimal number of edges of such a graph is at least k(k−1)/2.This bound is from the extremal example – a complete graph on k vertices, which is the smallest graph with chromatic number k. Thus, in chromatic number k, at least k(k−1)/2 edges are required. So, option C is necessarily true.
A graph can exhibit chromatic number k, but all degree less than k. Thus, we will again turn to examples of Mycielski graphs – vertices can be triangle-free, hence no high degree vertices, but nevertheless require more colors. So, option D is not necessarily true.
Q52 – Consider the operators ◊ and □ defined by
𝑎◊𝑏 = 𝑎+2𝑏, 𝑎□𝑏 = 𝑎𝑏, for positive integers.
Which of the following statements is/are TRUE?
(A) Operator ◊ obeys the associative law
(B) Operator □ obeys the associative law
(C) Operator ◊ over the operator □ obeys the distributive law
(D) Operator □ over the operator ◊ obeys the distributive law
Ans – (B, D)
Explanation – There are two operators we have: a⋄b=a + 2b and a□b=ab. The operator ⋄ is not associative.
(a⋄b)⋄c = a + 2b + 2c
a⋄(b⋄c) = a + 2b + 4c
so, option (A) is false.
The operator □ is multiplication and will be associative (a□b)□c=a□(b□c), so option (B) is true.
Next, we will see about the distributive laws. For ⋄ over □ we see that a⋄(b□c) is not equal to a⋄b□a⋄c.
a⋄(b□c) = a + 2bc
a⋄b□a⋄c = (a + 2b)(a + 2c) = a2 + 2(ac + ba) + 4bc.
so option (C) is false.
However, we can see that □ does satisfy the distributive law over ⋄. that is, a□(b⋄c)=(a□b)⋄(a□c) (D) is true.
a□(b⋄c) = ab + 2ac.
(a□b)⋄(a□c) = ab ⋄ ac = ab + 2ac.
Therefore, the true answers are (B) and (D).
Q53 – Consider two set-associative cache memory architectures: WBC, which uses the write back policy, and WTC, which uses the write through policy. Both of them use the LRU (Least Recently Used) block replacement policy. The cache memory is connected to the main memory.
Which of the following statements is/are TRUE?
(A) A read miss in WBC never evicts a dirty block
(B) A read miss in WTC never triggers a write back operation of a cache block to main memory
(C) A write hit in WBC can modify the value of the dirty bit of a cache block
(D) A write miss in WTC always writes the victim cache block to main memory before loading the missed block to the cache
Ans – (B, C)
Explanation – In this scenario, there are two cache architectures: WBC (Write-Back Cache) and WTC (Write-Through Cache), both using the LRU replacement policy.
In a Write-Back Cache, due to the LRU replacement policy, if there is an eviction of a dirty block, it will happen when there is a read miss. Therefore option (A) is not true.
In a write-through cache, all writes go to the main memory, which means that we do not ever mark cache blocks as dirty in a write-through cache. As such, during a read miss, we do not write back any block to main memory because there is nothing dirty. Therefore option (B) is true.
In a write-back cache, when we hit on a write, we update the cache block with the new data. We may also set the dirty bit. Thus, option (C) is true.
Option (D) is not true. A Write-Through Cache does not have dirty blocks, therefore, a write miss does not mean that the victim block must be written to memory.
Q54 – Consider a 512 GB hard disk with 32 storage surfaces. There are 4096 sectors per track and each sector holds 1024 bytes of data. The number of cylinders in the hard disk is _________.
Ans – (4096)
Explanation – Number of cylinders = Total disk size / data per cylinder
Number of cylinders = (512 * 10243)/(32 * 4096 * 1024)
There are 4096 cylinders
Q55 – The baseline execution time of a program on a 2 GHz single core machine is 100 nanoseconds (ns). The code corresponding to 90% of the execution time can be fully parallelized. The overhead for using an additional core is 10 ns when running on a multicore system.
Assume that all cores in the multicore system run their share of the parallelized code for an equal amount of time.
The number of cores that minimize the execution time of the program is ________.
Ans – (3)
Explanation – You have a program that takes 100 nanoseconds to run on a single-core computer.
Out of the total 100 ns, 90 ns of code can be accelerated through multi-core (parallel code) and 10 ns of the code always runs on a single core (serial code).
Also when you add one more core, it takes 10 ns of overhead (extra time to manage cores).
Now let’s say you use n cores.
Then the total time is – 10 ns for the serial part (cannot improve), 90/n ns for the parallel part (because you are distributing the work among cores),10 × (n – 1) ns extra overhead time because you are using more cores. So total time = 10 + 90/n + 10(n−1).
If n=1 → Time = 100 ns
If n=2 → Time= 10 + 45 + 10 = 65 ns
If n=3 → Time= 10 + 30 + 20 = 60 ns (minimum)
If n=4 → Time= 10 + 22.5 + 30 = 62.5 ns.
If n=5 → Time= 10 + 18 + 40 = 68 ns.
So, the optimal number of cores is 3 because it takes the least time.
Q56 – A given program has 25% load/store instructions. Suppose the ideal CPI (cycles per instruction) without any memory stalls is 2. The program exhibits 2% miss rate on instruction cache and 8% miss rate on data cache. The miss penalty is 100 cycles. The speedup (rounded off to two decimal places) achieved with a perfect cache (i.e., with NO data or instruction cache misses) is _________.
Ans – (3.00)
Explanation – Since all instructions go through the instruction cache, the instruction cache miss penalty per instruction is 0.02 x 100 = 2 cycles.
Only 25% of the instructions are load/store, so the data cache miss penalty per instruction is 0.25 x 0.08 x 100 = 2 cycles.
So, the actual CPI, or cycles per instruction (including memory stalls) is 2 (the ideal CPI) + 2 (the instruction stall penalty) + 2 (the data stall penalty) = 6.
The speedup = actual CPI / ideal CPI. Therefore, speedup = 6/2 = 3.00 (rounded off to two decimal places).
Q57 – Consider the following code snippet using the fork() and wait() system calls. Assume that the code compiles and runs correctly, and that the system calls run successfully without any errors.
int x = 3;
while(x > 0) {
fork();
printf(“hello”);
wait(NULL);
x–;
}
The total number of times the printf statement is executed is ___________.
Ans – (14)
Explanation –
Iteration 1 – When x = 3, fork happens.
So, parent and child, 2 processes are there and two printf command execute. Parent waits child to finish.
Iteration 2 –
When x = 2, fork happens again in parent and child.
So, 4 processes are there and four printf command execute. Parent waits child to finish.
Iteration 3 –
When x = 3, fork happens again in 4 processes.
So, 8 processes are there and eight printf command execute. Parent waits child to finish.
So, total 14 printf commands execute.
Q58 – Consider the entries shown below in the forwarding table of an IP router. Each entry consists of an IP prefix and the corresponding next hop router for packets whose destination IP address matches the prefix. The notation “/N” in a prefix indicates a subnet mask with the most significant N bits set to 1.
Prefix | Next hop router |
10.1.1.0/24 | R1 |
10.1.1.128/25 | R2 |
10.1.1.64/26 | R3 |
10.1.1.192/26 | R4 |
This router forwards 20 packets each to 5 hosts. The IP addresses of the hosts are 10.1.1.16, 10.1.1.72, 10.1.1.132, 10.1.1.191, and 10.1.1.205 . The number of packets forwarded via the next hop router R2 is _________.
Ans – (40)
Explanation – There are four routers R1, R2, R3, and R4. Each router has some prefixes defined. These prefixes tell us which IP address ranges the router can send packets to. So, based on the prefixes, we know which hosts (devices) each router can reach.
R1 prefix is 10.1.1.0/24
/24 → 32 – 24 = 8 bits for hosts → 28 = 256 addresses
IP block starts at: 10.1.1.0
Total 256 addresses: 10.1.1.0 to 10.1.1.255
R2 prefix is 10.1.1.128/25
/25 → 32 – 25 = 7 bits for hosts → 27 = 128 addresses
IP block starts at: 10.1.1.128
Total 128 addresses: 10.1.1.128 to 10.1.1.255
R3 prefix is 10.1.1.64/26
/26 → 32 – 26 = 6 bits for hosts → 26 = 64 addresses
IP block starts at: 10.1.1.64
Total 64 addresses: 10.1.1.64 to 10.1.1.127
R4 prefix is 10.1.1.192/26
/26 → 32 – 26 = 6 bits for hosts → 26 = 64 addresses
IP block starts at: 10.1.1.192
Total 64 addresses: 10.1.1.192 to 10.1.1.255
The router forwards 20 packets each to 5 hosts. The IP addresses of the hosts are given.
Router | Can send to IP address | Packets | Hosts |
R1 | 10.1.1.0 – 10.1.1.255 | 20 | 10.1.1.16 |
R2 | 10.1.1.128 – 10.1.1.255 | 20 | 10.1.1.132 |
20 | 10.1.1.191 | ||
R3 | 10.1.1.64 – 10.1.1.127 | 20 | 10.1.1.72 |
R4 | 10.1.1.192 – 10.1.1.255 | 20 | 10.1.1.205 |
Note – Can R1 send to all the hosts, because it can send from 10.1.1.0 to 10.1.1.255. Means every host is in their IP address.
The answer is NO, because routers follow the Longest Prefix Match rule.
That means the router checks all matching entries for an IP and selects the one with the longest (most specific) prefix.
For example – Host with IP address 10.1.1.205 matches with 10.1.1.192/26 (Longest prefix).
Q59 – Let 𝐺 = (𝑉, Σ, 𝑆, 𝑃) be a context-free grammar in Chomsky Normal Form with Σ = {𝑎, 𝑏, 𝑐} and 𝑉 containing 10 variable symbols including the start symbol 𝑆. The string 𝑤 = 𝑎30𝑏30𝑐30 is derivable from 𝑆. The number of steps (application of rules) in the derivation 𝑆→*𝑤 is _________.
Ans – (179)
Explanation – The grammar generates the string w = a³⁰b³⁰c³⁰, which is 90 characters long.
Every production rule in CNF is of the form A → BC (where A, B, and C are variables), or A → a (where a is the terminal symbol).
Since we need to generate 90 terminal symbols (30 a’s, 30 b’s, and 30 c’s), we will need to have 90 applications of rules such as A → a, one for each terminal.
To the parse tree derivation, we need a binary tree which combines all variables together. A binary tree with 90 leaves (terminals) needs 89 internal nodes, which means we need 89 applications of the rules such as A → BC.
Thus, the number of total steps in the derivation is 90 (terminals) + 89 (internal nodes) = 179 steps.
Q60 – The number of edges present in the forest generated by the DFS traversal of an undirected graph 𝐺 with 100 vertices is 40. The number of connected components in 𝐺 is _________.
Ans – (60)
Explanation – In a DFS forest, each tree represents one connected component. A tree with n vertices has exactly n – 1 edges.
Now, suppose the number of connected components is k.
- Each of those k trees contributes nᵢ – 1 edges.
Total number of edges in all trees => ∑(ni – 1) = 100 – k
=> 40 = 100 – k
Then, k = 60
Q61 – Consider the following two regular expressions over the alphabet {0, 1}:
𝑟 = 0*+1*
𝑠 = 01*+10*
The total number of strings of length less than or equal to 5, which are neither in 𝑟 nor in 𝑠, is _________.
Ans – (44)
Explanation – The total number of strings of length less than or equal to 5 over the alphabets {0, 1} is = 1 + 2 + 4 + 8 + 16 + 32 = 63 strings.
Strings in r = 0* + 1* = ϵ, 0, 00, 000, 0000, 00000, 1, 11, 111, 1111, 11111. There is total 11 strings.
Strings in s = 01* + 10* = 0, 01, 011, 0111, 01111, 1, 10, 100, 1000, 10000. There is total 10 strings
Strings in r and s = 11 + 10 – 2 = 19 strings [because 0 and 1 strings are in both r and s]
The total number of strings of length less than or equal to 5, which are neither in 𝑟 nor in 𝑠, is 63 – 19 = 44 strings.
Q62 – Consider a memory management system that uses a page size of 2 KB. Assume that both the physical and virtual addresses start from 0. Assume that the pages 0, 1, 2, and 3 are stored in the page frames 1, 3, 2, and 0, respectively. The physical address (in decimal format) corresponding to the virtual address 2500 (in decimal format) is _________.
Ans – (6596)
Explanation –
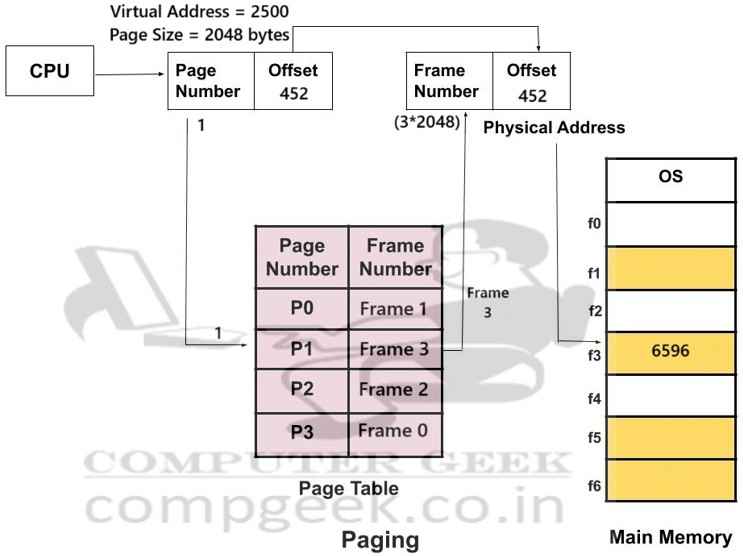
The CPU produces a logical address (also called a virtual address).
Logical (virtual) address is split into two parts
- Page Number
- Offset within that page
Virtual address = 2500 (in decimal)
Page size = 2 KB = 2048 bytes
Page number = 2500 ÷ 2048 = 1 (quotient)
Offset = 2500 % 2048 = 452
So, virtual address 2500 belongs to virtual page 1, with offset = 452.
Page to frame mapping:
Page 0 → Frame 1
Page 1 → Frame 3
Page 2 → Frame 2
Page 3 → Frame 0
Physical address = (frame number x page size) + offset
= (3 x 2048) + 452
= 6144 + 452
= 6596
Q63 – A bag contains 10 red balls and 15 blue balls. Two balls are drawn randomly without replacement. Given that the first ball drawn is red, the probability (rounded off to 3 decimal places) that both balls drawn are red is _________.
Ans – (0.370 to 0.380)
Explanation – There are 25 balls of which 10 are red balls and 15 are blue balls. Two balls are drawn randomly without replacement.
The first one is red, so there are 24 balls of which 9 are red balls and 15 are blue balls
Probability = 9/24 = 0.375.
So, 0.375 is exactly between 0.370 to 0.380.
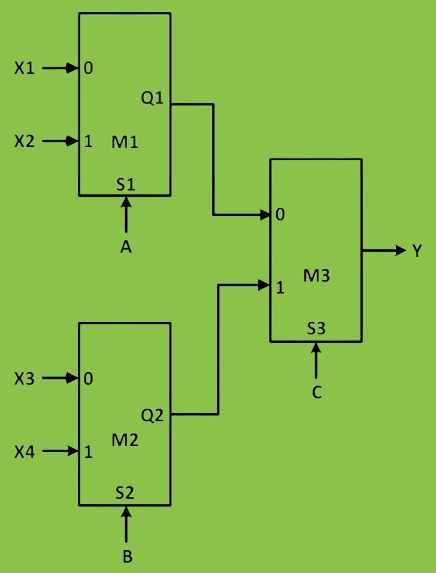
Q64 – Consider a digital logic circuit consisting of three 2-to-1 multiplexers M1, M2, and M3 as shown below. X1 and X2 are inputs of M1. X3 and X4 are inputs of M2.
A, B, and C are select lines of M1, M2, and M3, respectively.

For an instance of inputs X1=1, X2=1, X3=0, and X4=0, the number of combinations of A, B, C that give the output Y=1 is _________.
Ans – (4)
Explanation –
We are given, X1 = 1 and X2 = 2, So it does not matter if A is 0 or 1.
Also, X3 = 0 and X4 = 0, So, it does not matter if B is 0 or 1.
Now, we are given that output Y = 1. So, C must be 0 because
The equation is, Y = C’.Q1 + C.Q2 = 1.1 + 0.0 = 1
A | B | C | Y |
0 | 0 | 0 | 1 |
0 | 1 | 0 | 1 |
1 | 0 | 0 | 1 |
1 | 1 | 0 | 1 |
So, 4 combinations are there.
Q65 – Consider sending an IP datagram of size 1420 bytes (including 20 bytes of IP header) from a sender to a receiver over a path of two links with a router between them.
The first link (sender to router) has an MTU (Maximum Transmission Unit) size of 542 bytes, while the second link (router to receiver) has an MTU size of 360 bytes.
The number of fragments that would be delivered at the receiver is ________.
Ans – (6)
Explanation – 
From sender to router, IP datagram = 1420 bytes
Including IP header = 20 bytes
Payload = 1420 – 20 = 1400 bytes
Next, MTU = 542 bytes
Each fragment without payload= 542 – 20 = 522 bytes
Number of fragments = ⎾1400/522⏋ = 3 fragments
From router to receiver, MTU = 360 bytes
Each fragment without payload = 360 – 20 = 340 bytes
First fragments = ⎾522/340⏋ = 2
Second fragments = ⎾522/340⏋ = 2
Third fragment = ⎾356/340⏋ = 2 why?
Because sender to router, payload is 1400 bytes and it equal to 522 bytes + 522 bytes + 356 bytes.
Total number of fragments from router to receiver is 6.



 (A) (i)
(A) (i)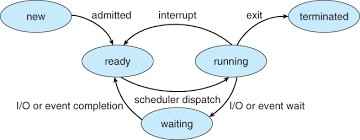
 The value of the expression 3+1+5∗2/7+2−4−7−6/2 as per the above rules is __________
The value of the expression 3+1+5∗2/7+2−4−7−6/2 as per the above rules is __________