Branch and Bound Algorithm

Introduction

.

The Branch and Bound algorithm is a powerful technique used to solve optimization problems, especially when the solution space is large and complex.

It systematically explores all possible solutions by dividing the problem into smaller subproblems (branching) and uses bounds to eliminate subproblems that cannot lead to an optimal solution (bounding).

This approach is often applied to combinatorial problems like the Traveling Salesman Problem (TSP), knapsack problem, and integer programming.

.

History of the Branch and Bound Algorithm

The “Branch and Bound” method was formally introduced by British researchers Alisa H. Land and A. G. Doig in their 1960 paper, where they applied the technique to integer programming.

Their work laid the groundwork for the systematic exploration of solution spaces by branching into subproblems and using bounds to prune non-promising branches.

Around the same time, Richard Bellman contributed to dynamic programming, which shares some conceptual similarities with Branch and Bound. Bellman’s work on decision processes influenced the development of methods for solving optimization problems, including Branch and Bound.

Working of Branch and Bound

1. Branching:
   • The problem is broken down into smaller subproblems.
   • Each subproblem represents a potential solution or part of a solution.
   • The process of branching continues until the problem is simplified to a point where it can be easily solved.
2. Bounding:
   • For each subproblem, calculate an upper or lower bound on the possible solution.
   • If a bound indicates that a subproblem cannot produce a better solution than the current best-known solution, that branch is pruned (discarded).
3. Pruning:
   • Pruning is the process of eliminating branches that cannot lead to an optimal solution.
   • By pruning, the algorithm reduces the number of subproblems that need to be explored, making the search more efficient.
4. Backtracking:
   • After exploring one branch, the algorithm backtracks to explore other branches, ensuring that all potential solutions are considered.
   • The best-known solution is updated whenever a better solution is found.

Please don’t misunderstand this problem by Divide & Conquer. There is a difference between Divide & Conquer Vs Branch & Bound.

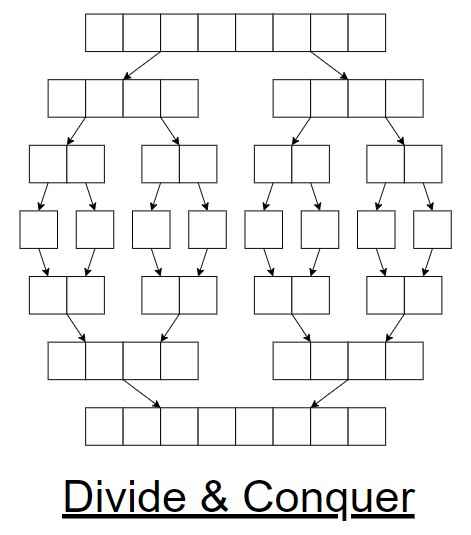
Divide and Conquer is a strategy used in algorithm design that breaks a problem into smaller, independent subproblems, solves each subproblem recursively, and then combines their solutions to solve the original problem.

.

This approach is particularly effective when the subproblems are simpler versions of the original problem and can be solved independently.

Common examples include algorithms like Merge Sort, Quick Sort, and Binary Search, where the problem is divided into smaller parts, solved separately, and then combined to get the final solution.

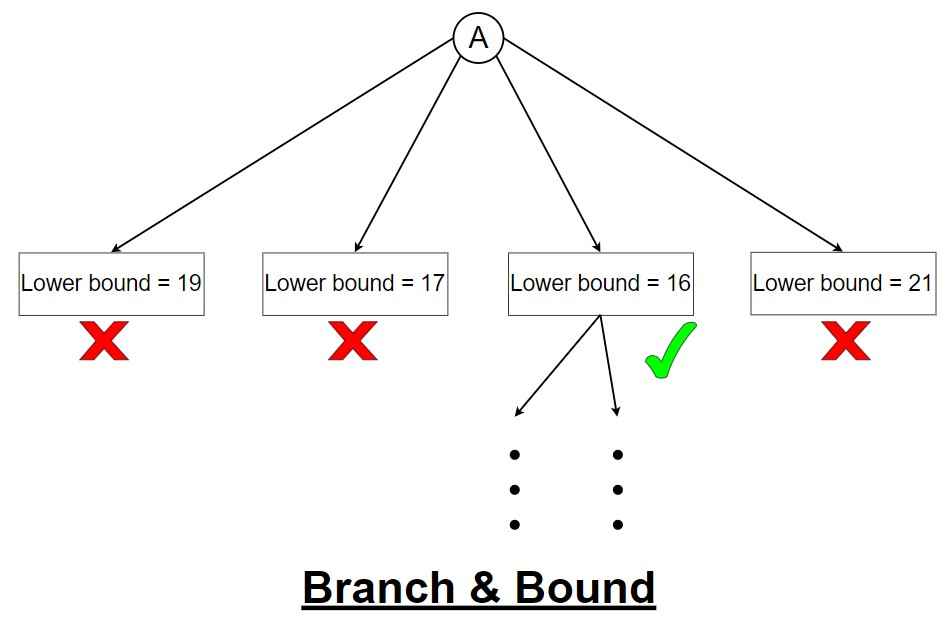
Branch and Bound on the other hand, is an algorithmic method used primarily for solving optimization problems. It systematically explores the solution space by dividing it into smaller branches, and uses bounds to prune branches that cannot lead to an optimal solution.

.

The idea is to explore the most promising branches first while discarding others, making the search more efficient.

This method is especially useful for problems like the Traveling Salesman Problem and the Knapsack Problem, where the goal is to find the best possible solution among many possible options.

While Divide and Conquer is focused on dividing the problem into independent subproblems, Branch and Bound focuses on exploring a solution space and pruning unnecessary parts based on bounds. Both are powerful techniques but are applied in different contexts depending on the nature of the problem.

.

Also, there is difference between Backtracking and Branch & Bound approach.

Backtracking is an algorithmic technique used to solve problems incrementally by building a solution piece by piece. If a piece is found to lead to a solution that does not meet the criteria or constraints of the problem, the algorithm “backtracks” by removing the last piece and trying another path.

.

It means by backtracking, we solve one path and the path does not meet with the constraints of the problem then we backtrack but, in the “branch & bound” approach, we never go onto that path that doesn’t meet the constraints of the problem, and we can predict it by bounding (lower bound or upper bound).

.

Here are some classic problems that can be solved using the Branch and Bound algorithm:

1. Traveling Salesman Problem (TSP)

• Problem Statement – Given a list of cities and the distances between each pair of cities, find the shortest possible route that visits each city exactly once and returns to the origin city.
• Branching – Select the next city to visit.
• Bounding – Calculate the lower bound of the cost for a partial tour.
• Application of Branch and Bound – This problem is typically solved by exploring all possible routes and pruning those routes that exceed the current best-known solution’s cost.

2. 0/1 Knapsack Problem

• Problem Statement – Given a set of items, each with a weight and a value, determine the number of each item to include in a collection so that the total weight is less than or equal to a given limit and the total value is maximized.
• Branching – Decide whether to include an item in the knapsack.
• Bounding – Calculate the upper bound of the maximum possible value with the remaining items.
• Application of Branch and Bound – The algorithm explores combinations of items, pruning combinations that cannot yield a better solution than the current best.

3. Integer Linear Programming (ILP)

• Problem Statement – Optimize a linear objective function subject to linear equality and inequality constraints, where some or all of the variables are required to be integers.
• Branching – Split the problem into subproblems by fixing an integer variable.
• Bounding – Use the solution of the relaxed linear program (where integer constraints are removed) to obtain bounds.
• Application of Branch and Bound – This method is used to find the optimal integer solution by exploring and pruning subproblems based on bounds.

4. Job Scheduling Problem

• Problem Statement – Assign jobs to machines in a way that minimizes the maximum completion time.
• Branching – Assign jobs to different machines.
• Bounding – Calculate the minimum possible completion time for a partial schedule.
• Application of Branch and Bound – The algorithm explores different job assignments and prunes those that cannot improve the current best-known completion time.

.

Time Complexity

The time complexity of the Branch and Bound algorithm can vary depending on the specific problem and the bounding function used.

In the worst case, it can be exponential, O(b^d), where b is the branching factor (the number of subproblems generated at each step) and d is the depth of the solution space (the number of decisions to reach a solution). This is because, in the worst case, the algorithm might have to explore all possible branches.

.

Space Complexity

The space complexity of Branch and Bound also depends on the specific problem but is generally O(b × d) or O(b^d).

It requires space to store all the nodes in the search tree, which can be large if the branching factor or depth is significant. However, if an iterative approach or a priority queue is used, the space complexity can be reduced to a more manageable level.

.

Advantages

1. It guarantees finding the optimal solution because it systematically explores the entire solution space, pruning suboptimal branches.
2. It significantly reduces the number of solutions that need to be evaluated, making it more efficient than brute force methods.
3. It can be applied to a wide range of combinatorial optimization problems like the Traveling Salesman Problem, Knapsack Problem, Job Scheduling, etc
4. It is particularly useful for problems with specific constraints, as it effectively prunes solutions that violate these constraints.

.

Disadvantages

1. The worst-case time complexity can still be exponential, making it impractical for very large problem instances.
2. It can require significant memory to store nodes and paths, especially for large problems with high branching factors.
3. Implementing the Branch and Bound algorithm can be complex, especially when designing effective bounding functions for pruning.
4. The efficiency of Branch and Bound heavily depends on the quality of the bounding function, which may not always be favourable.