Introduction
The Single Source Shortest Path (SSSP) algorithm is a fundamental concept in graph theory and algorithms.
It aims to find the shortest path from a single source vertex to all other vertices in a graph.
The title of “father” of the Single Source Shortest Path (SSSP) algorithms is often attributed to Edsger W. Dijkstra in 1956.
Among several SSSP algorithms, Dijkstra’s algorithm and bellman ford algorithms are widely used for its efficiency and simplicity.
.
Notations
G – A graph
V – The set of vertices in G.
E – The set of edges in G.
w(u,v) – The weight or cost associated with the edge (u,v).
dist[v] – The distance from a designated source vertex s to vertex v.
.
Definition
The Single Source Shortest Path problem seeks to determine, for each vertex v in the graph G, the minimum distance dist[v] from a specified source vertex A.
The minimum distance is defined as the smallest sum of edge weights along a path from the source A to the vertex v among all possible paths.
.
Mathematical Representation
The objective is to find dist[v] for every v in set of vertices V such that
dist[v] = min(dist[u] + w(u,v))
where the minimum is taken over all vertices u in V, and w(u,v) represents the weight of the edge connecting u to v.
The solution to the SSSP problem provides a set of distances dist[v] that satisfies the minimization condition, revealing the shortest paths from the source vertex A to all other vertices in the graph.
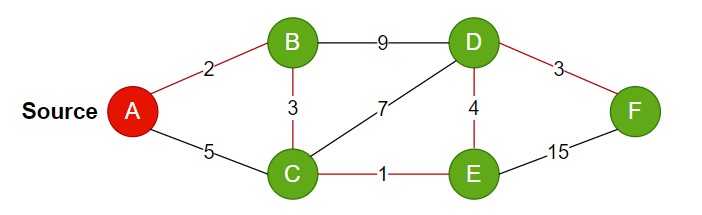
The shortest distance between the vertex F with respect to A is 13.
.
SSSP Algorithm
- Start at the source vertex.
- Mark the distance to itself as 0 and all other vertices as infinity.
- For the current vertex, consider all of its neighbours and calculate their tentative distances through the current vertex.
- If the newly calculated tentative distance is less than the current assigned value, update the distance.
- Mark the current vertex as visited.
- Repeat steps 3-5 until all vertices are visited.
.
Types of Algorithms in SSSP
There are two algorithms, Dijkstra and Bellman ford.
.
- Dijkstra’s algorithm – is a popular algorithm for solving the Single Source Shortest Path (SSSP) problem in a graph with non-negative edge weights. It efficiently finds the shortest paths from a specified source vertex to all other vertices in the graph. Dijkstra’s algorithm is widely used in various applications, such as network routing and navigation systems, where finding the shortest paths from a source to all destinations is crucial.
- Bellman-Ford Algorithm – is another approach to solving the Single Source Shortest Path (SSSP) problem, but it can handle graphs with edges having negative weights.
This algorithm is less efficient than Dijkstra’s algorithm but is more versatile in handling a wider range of graphs.
Bellman-Ford is used in routing protocols like RIP (Routing Information Protocol), telecommunication network planning, resource management in cloud computing, game development, urban planning etc.
.
Applications of SSSP Algorithm
- Negative Cycles – SSSP algorithms like Bellman-Ford can detect negative cycles in a graph. A negative cycle is a cycle where the sum of the edge weights is negative. Detecting negative cycles is crucial in scenarios like financial modelling, where it helps identify arbitrage opportunities.
- Heuristic Approaches – In certain scenarios, heuristic approaches like A* search algorithm are used for pathfinding. These algorithms combine the benefits of informed search and heuristics to find efficient paths.
- Parallelization – Parallel algorithms for SSSP, especially for large graphs, have been developed. These leverage parallel computing architectures to speed up the computation of shortest paths.
- Applications Beyond Networks – While SSSP algorithms are commonly associated with network-related problems, they find applications in diverse fields such as biology (protein-protein interaction networks), transportation (finding optimal routes), and social network analysis.
- Weighted vs. Unweighted Graphs – SSSP algorithms are designed for weighted graphs where edges have associated costs or distances. For unweighted graphs, simpler algorithms like Breadth-First Search (BFS) can be used to find shortest paths.
- Dynamic Graphs – Handling dynamic graphs (graphs that change over time) is an active area of research. Algorithms must adapt to additions or deletions of edges or vertices.
- Path Reconstruction – Some SSSP algorithms, like Dijkstra’s, can be modified to reconstruct the actual paths along with the shortest distances. This information is valuable in understanding the route taken.
- Graph Theory Applications – SSSP algorithms contribute to solving problems in graph theory, where understanding the relationships and connectivity between vertices is fundamental.
Test Yourself
Q1- What distinguishes Prim’s algorithm and Single Source Shortest Path (SSSP) algorithms, both of which begin with a designated starting vertex?
Yes, in Prim’s algorithm, the process starts with an initial arbitrary vertex and Single Source Shortest Path (SSSP) algorithms, such as Dijkstra’s algorithm or Bellman-Ford algorithm, also start from a specific starting vertex.
But the primary differences lie in their objectives and how they traverse the graph.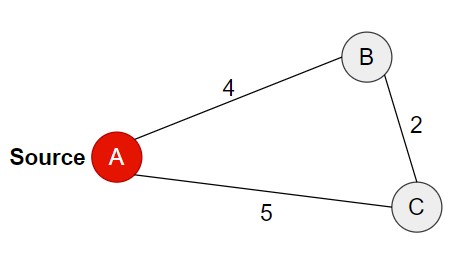
Prim’s Algorithm – Focuses on building a Minimum Spanning Tree by repeatedly selecting the smallest edge that connects the current tree to a new vertex.
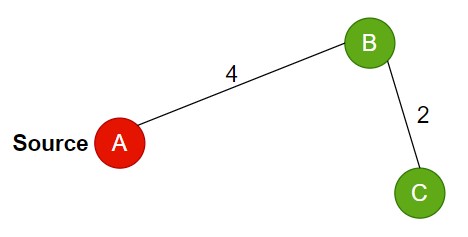
Single Source Shortest Path Algorithms – Concentrate on finding the shortest paths from a single source vertex to all other vertices in the graph by iteratively evaluating and updating the shortest distances.
Q2- Explain the significance of the Single Source Shortest Path (SSSP) algorithm in real-world applications.
The SSSP algorithm determines the shortest paths from a source vertex to all other vertices, crucial in various fields like network routing, navigation, finance, and transportation for optimal route planning.
Q3- Explain how parallelization techniques can enhance the efficiency of Single Source Shortest Path algorithms for large graphs.
Parallel algorithms leverage multiple computing units to perform simultaneous computations, reducing the time complexity for computing shortest paths in large graphs.
Q4- Discuss the challenges and considerations involved in handling dynamic graphs using Single Source Shortest Path algorithms.
Dynamic graphs involve constant changes in edges/vertices, requiring algorithms to adapt efficiently without recomputing the entire graph.
Q5- In what ways do Single Source Shortest Path algorithms contribute to advancing research in graph theory?
These algorithms provide insights into connectivity, distances, and relationships between vertices, contributing to analyzing graph structures and properties.
Q6- What role does path reconstruction play in SSSP algorithms?
Enhances graph visualization
Speeds up computation
Reduces time complexity
Prevents negative cycles
Ans – (1)
Explanation – Path reconstruction is important in Single-Source Shortest Path (SSSP) algorithms because it helps to determine the shortest path from the source vertex to all other vertices in the graph. This feature assists in enhancing graph visualization and aiding students in understanding the concept of shortest paths. So, the correct answer is (1) Enhances graph visualization






