Understanding the Fractional Knapsack Algorithm
.

.
Introduction
In the realm of algorithms, there’s a fascinating problem-solving technique known as the Fractional Knapsack Algorithm. This algorithm was solved by Greedy Method in less time.
This algorithm plays a crucial role in solving optimization problems where you must choose items to maximize a value while staying within a limited capacity, just like packing a knapsack (bag) for a journey or a thief inside a jewelry store with a knapsack of limited capacity.
In this article, we will learn about the Fractional Knapsack Algorithm in detail, breaking it down in simple terms, so even beginners can grasp the concept with ease.
.
Definition
Fractional Knapsack is like packing a backpack with limited space to get the most value.
You have different items, each with a weight and value. The goal is to select items and decide how much of each item to take (even fractions because this is fractional knapsack) so that the total value is as high as possible without going over the knapsack’s weight limit.
It’s like a strategy game of making the best choices to get the most valuable items while not carrying too much weight.
.
Working of the Fractional Knapsack Algorithm
The Fractional Knapsack Algorithm works in a step-by-step manner:
1. Calculate the value-to-weight ratio for each item
2. Arrange the items in non-ascending order, so the items with the highest value-to-weight ratio come first.
3. Start with an empty knapsack.
4. Select items one by one – Beginning with the item with the highest value-to-weight ratio, add items to the knapsack until it’s full. If an item can’t fit entirely, add a fraction of it to fill the knapsack to capacity.
5. Continue this process and after knapsack is full, specify the maximum value.
.
Algorithm of Fractional Knapsack
Two arrays: v (values of items) and w (weights of items).
An integer W representing the weight capacity of the knapsack.
1. Initialize an array p to store the value-to-weight ratios for each item.
2. For each item i from 1 to the size of the arrays v and w
=>Calculate the value-to-weight ratio: p[i] = v[i] / w[i].
3. Sort the array p in non-ascending order.
4. Initialize a variable i to 1
5. While the knapsack’s weight capacity W is greater than 0
6. Do the following
- Calculate the amount to add to the knapsack
- amount = min(W, w[i])
- Reduce the knapsack’s weight capacity: W = W – amount.
- Move to the next item: i = i + 1.
7. Return the array, which specifies the fraction of each item to include in the knapsack while maximizing the total value.
Example
Suppose you have a knapsack with a weight capacity (w) of 15 Kgs and the following items:
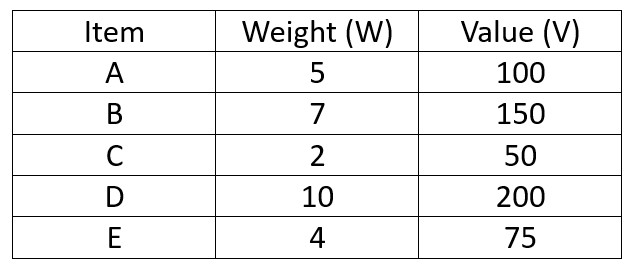
.
Let’s use the Fractional Knapsack Algorithm to determine the best combination of items for the knapsack.
- Calculate value-to-weight ratios
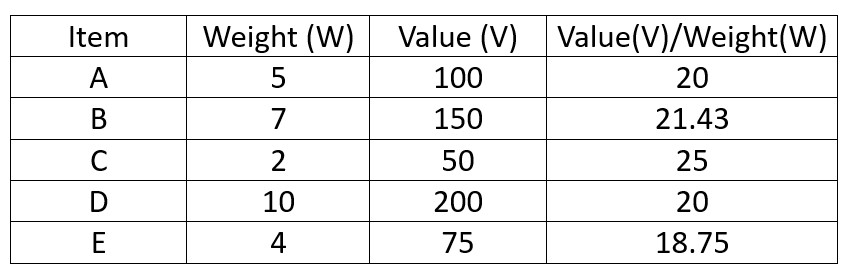
.
- Sort items by value-to-weight ratio in descending order: C, B, A, D, E.
- Initialize the knapsack with a current weight of 0 and a total value of 0.
- Start with item C (value 50, weight 2)
- It can be fully added to the knapsack, and the knapsack’s current weight becomes 2 Kgs.
- The total value is updated to 50.
- Knapsack remaining weight = 15 – 2 = 13 Kgs.
- Move to item B (value 150, weight 7).
- It can be fully added to the knapsack, and the knapsack’s current weight becomes 2 + 7 = 9 Kgs.
- The total value is updated to 50 + 150 = 200.
- Knapsack remaining weight = 13 – 7 = 6 Kgs
Move to item A (value 100, weight 5)
It can be fully added to the knapsack, and the knapsack’s current weight becomes 9 + 5 = 14 Kgs.
The total value is updated to 200 + 100 = 300.
Knapsack remaining weight = 6 – 5 = 1 Kgs.
Move to item D (value 200, weight 10)
It cannot be fully added to the knapsack, but a fraction of 1 kg is added and the knapsack’s current weight becomes 14 + 1 = 15 Kgs.
1 kg value = 200/10 = 20
The total value is updated to 300 + 20 = 320.
Knapsack remaining weight = 1 – 1 = 0 Kg
- The knapsack is now full, and the total value is 320.
.
Source Code for Fractional Knapsack Problem
// COMPUTER GEEK – compgeek.co.in
// Write a program for Fractional Knapsack Problem
#include <stdio.h>
// Structure to represent items
struct Item
{
int weight;
int value;
};
// Function to compare items by value-to-weight ratio for sorting
int compare(const void *a, const void *b)
{
double ratioA = ((struct Item *)a)->value / (double)((struct Item *)a)->weight;
double ratioB = ((struct Item *)b)->value / (double)((struct Item *)b)->weight;
return (ratioB – ratioA > 0) ? 1 : -1;
}
// Function to solve Fractional Knapsack
void fractionalKnapsack(struct Item items[], int n, int capacity)
{
// Sort items by value-to-weight ratio in non-increasing order
qsort(items, n, sizeof(struct Item), compare);
int currentWeight = 0; // Current weight in the knapsack
double finalValue = 0.0; // Final value of items in the knapsack
// Initialize the solution array with zeros
double solution[n];
for (int i = 0; i < n; i++)
{
solution[i] = 0.0;
}
// Fill the knapsack while the capacity allows
for (int i = 0; i < n; i++)
{
if (currentWeight + items[i].weight <= capacity)
{
// Take the whole item if it fits
solution[i] = 1.0;
currentWeight += items[i].weight;
finalValue += items[i].value;
}
else
{
// Take a fraction of the item
solution[i] = (double)(capacity – currentWeight) / items[i].weight;
finalValue += solution[i] * items[i].value;
break; // Knapsack is full
}
}
// Print the result
printf(“The maximum value obtained = %.2lf\n”, finalValue);
printf(“Item fractions in the knapsack:\n”);
for (int i = 0; i < n; i++)
{
printf(“Item %d: %.2lf\n”, i + 1, solution[i]);
}
}
int main()
{
int n, capacity;
// Input the number of items and the capacity of the knapsack
printf(“Enter the number of items: “);
scanf(“%d”, &n);
printf(“Enter the capacity of the knapsack: “);
scanf(“%d”, &capacity);
struct Item items[n];
// Input item details: weight and value
for (int i = 0; i < n; i++)
{
printf(“Enter the weight of item %d: “, i + 1);
scanf(“%d”, &items[i].weight);
printf(“Enter the value of item %d: “, i + 1);
scanf(“%d”, &items[i].value);
}
// Solve the Fractional Knapsack problem
fractionalKnapsack(items, n, capacity);
return 0;
}
// COMPUTER GEEK – compgeek.co.in
// Write a program for Fractional Knapsack Problem
#include <iostream>
#include <vector>
#include <algorithm>
// Structure to represent items
struct Item
{
int weight;
int value;
};
// Function to compare items by value-to-weight ratio for sorting
bool compare(const Item& a, const Item& b)
{
double ratioA = static_cast<double>(a.value) / a.weight;
double ratioB = static_cast<double>(b.value) / b.weight;
return ratioA > ratioB;
}
// Function to solve Fractional Knapsack
void fractionalKnapsack(std::vector<Item>& items, int capacity)
{
// Sort items by value-to-weight ratio in non-increasing order
std::sort(items.begin(), items.end(), compare);
int currentWeight = 0; // Current weight in the knapsack
double finalValue = 0.0; // Final value of items in the knapsack
// Initialize the solution array with zeros
std::vector<double> solution(items.size(), 0.0);
// Fill the knapsack while the capacity allows
for (int i = 0; i < items.size(); i++)
{
if (currentWeight + items[i].weight <= capacity)
{
// Take the whole item if it fits
solution[i] = 1.0;
currentWeight += items[i].weight;
finalValue += items[i].value;
}
else
{
// Take a fraction of the item
solution[i] = static_cast<double>(capacity – currentWeight) / items[i].weight;
finalValue += solution[i] * items[i].value;
break; // Knapsack is full
}
}
// Print the result
std::cout << “The maximum value obtained = ” << finalValue << std::endl;
std::cout << “Item fractions in the knapsack:” << std::endl;
for (int i = 0; i < items.size(); i++)
{
std::cout << “Item ” << i + 1 << “: ” << solution[i] << std::endl;
}
}
int main()
{
int n, capacity;
// Input the number of items and the capacity of the knapsack
std::cout << “Enter the number of items: “;
std::cin >> n;
std::cout << “Enter the capacity of the knapsack: “;
std::cin >> capacity;
std::vector<Item> items(n);
// Input item details: weight and value
for (int i = 0; i < n; i++)
{
std::cout << “Enter the weight of item ” << i + 1 << “: “;
std::cin >> items[i].weight;
std::cout << “Enter the value of item ” << i + 1 << “: “;
std::cin >> items[i].value;
}
// Solve the Fractional Knapsack problem
fractionalKnapsack(items, capacity);
return 0;
}
// COMPUTER GEEK – compgeek.co.in
// Write a program for Fractional Knapsack Problem
import java.util.ArrayList;
import java.util.Collections;
import java.util.Comparator;
import java.util.List;
import java.util.Scanner;
class Item
{
int weight;
int value;
public Item(int weight, int value)
{
this.weight = weight;
this.value = value;
}
}
public class FractionalKnapsack
{
// Comparator to sort items by value-to-weight ratio in non-increasing order
static class ItemComparator implements Comparator<Item>
{
public int compare(Item a, Item b) {
double ratioA = (double) a.value / a.weight;
double ratioB = (double) b.value / b.weight;
return Double.compare(ratioB, ratioA);
}
}
public static void main(String[] args)
{
Scanner scanner = new Scanner(System.in);
System.out.print(“Enter the number of items: “);
int n = scanner.nextInt();
System.out.print(“Enter the capacity of the knapsack: “);
int capacity = scanner.nextInt();
List<Item> items = new ArrayList<>();
// Input item details: weight and value
for (int i = 0; i < n; i++)
{
System.out.print(“Enter the weight of item ” + (i + 1) + “: “);
int weight = scanner.nextInt();
System.out.print(“Enter the value of item ” + (i + 1) + “: “);
int value = scanner.nextInt();
items.add(new Item(weight, value));
}
// Sort items by value-to-weight ratio in non-increasing order
Collections.sort(items, new ItemComparator());
int currentWeight = 0;
double finalValue = 0.0;
// Initialize the solution array with zeros
double[] solution = new double[n];
// Fill the knapsack while the capacity allows
for (int i = 0; i < n; i++)
{
if (currentWeight + items.get(i).weight <= capacity)
{
// Take the whole item if it fits
solution[i] = 1.0;
currentWeight += items.get(i).weight;
finalValue += items.get(i).value;
}
else
{
// Take a fraction of the item
solution[i] = (double) (capacity – currentWeight) / items.get(i).weight;
finalValue += solution[i] * items.get(i).value;
break; // Knapsack is full
}
}
// Print the result
System.out.println(“The maximum value obtained = ” + finalValue);
System.out.println(“Item fractions in the knapsack:”);
for (int i = 0; i < n; i++)
{
System.out.println(“Item ” + (i + 1) + “: ” + solution[i]);
}
}
}
# COMPUTER GEEK – compgeek.co.in
# Write a program for Fractional Knapsack Problem
class Item:
def __init__(self, weight, value):
self.weight = weight
self.value = value
def fractional_knapsack(items, capacity):
# Sort items by value-to-weight ratio in non-increasing order
items.sort(key=lambda x: x.value / x.weight, reverse=True)
current_weight = 0
final_value = 0.0
# Initialize the solution array with zeros
solution = [0.0] * len(items)
# Fill the knapsack while the capacity allows
for i, item in enumerate(items):
if current_weight + item.weight <= capacity:
# Take the whole item if it fits
solution[i] = 1.0
current_weight += item.weight
final_value += item.value
else:
# Take a fraction of the item
solution[i] = (capacity – current_weight) / item.weight
final_value += solution[i] * item.value
break # Knapsack is full
# Print the result
print(“The maximum value obtained = {:.2f}”.format(final_value))
print(“Item fractions in the knapsack:”)
for i, fraction in enumerate(solution):
print(“Item {}: {:.2f}”.format(i + 1, fraction))
if __name__ == “__main__”:
n = int(input(“Enter the number of items: “))
capacity = int(input(“Enter the capacity of the knapsack: “))
items = []
# Input item details: weight and value
for i in range(n):
weight = int(input(f”Enter the weight of item {i + 1}: “))
value = int(input(f”Enter the value of item {i + 1}: “))
items.append(Item(weight, value))
# Solve the Fractional Knapsack problem
fractional_knapsack(items, capacity)
Time Complexity of Fractional Knapsack problem
The Fractional Knapsack problem, as traditionally solved by the greedy approach, has a time complexity of O(n log n) due to the sorting step, where ‘n’ is the number of items to be considered.
.
Note –
However, Fractional Knapsack problem can be solved using dynamic programming. It has a different time complexity.
In dynamic programming, we consider all possible combinations of items to determine the optimal solution. The time complexity of dynamic programming for the Fractional Knapsack problem is O(nW), where ‘n’ is the number of items, and ‘W’ is the maximum weight the knapsack can hold. This will come when we study dynamic programming.
.
Space Complexity of Fractional Knapsack problem
The space complexity for this approach is O(n) since you need an additional space array of size ‘n’ to store the value-to-weight ratios of each item.
Note –
In the dynamic programming approach, the space complexity is typically O(nW), where ‘n’ is the number of items and ‘W’ is the maximum weight capacity of the knapsack. This will come when we study dynamic programming.
.
Advantages of Fractional Knapsack problem
- Simplicity – The Fractional Knapsack Algorithm is easy to understand and implement.
- Efficiency – It provides a relatively good solution quickly, making it suitable for large datasets.
- Flexibility – It allows fractions of items to be included, providing a realistic approach to real-world scenarios.
.
Disadvantages of Fractional Knapsack problem
- The Fractional Knapsack problem assumes that items can be divided into fractions, which may not always be practical or realistic. 15 kg gold powder is hard to get in the above example.
.
Applications of Fractional Knapsack problem
The Fractional Knapsack Algorithm finds applications in various domains, including:
- Determining the best investments to maximize returns within a budget.
- Optimizing the selection of materials for product assembly.
- Allocating resources efficiently in projects or operations.
- Farmers can apply the algorithm to optimize crop planting and resource allocation for maximum yield and profit.
- Selecting cargo for efficient shipping or airline baggage allocation.
Test Yourself
Q1- When does the Fractional Knapsack Algorithm provide a suboptimal solution?
The algorithm can provide suboptimal solutions when items cannot be divided into fractions, and the greedy approach may not work correctly.
Q2- What is the significance of the “fraction” in the Fractional Knapsack Algorithm, and when is it relevant?
The “fraction” means that items can be taken partially. It’s relevant when an item’s weight exceeds the remaining capacity of the knapsack.
Q3- How does the dynamic programming approach to the Fractional Knapsack Algorithm differ from the greedy approach in terms of time complexity?
The dynamic programming approach considers all possible combinations and has a time complexity of O(nW), which can be much slower for large datasets compared to the greedy approach’s O(n log n).
Q4- What is the goal of the Fractional Knapsack Algorithm?
1. To minimize the weight of selected items
2. To maximize the value of selected items
3. To maximize the weight of selected items
4. To minimize the value of selected items
Ans – (2)
Explanation – The primary objective of the algorithm is to maximize the total value of items chosen while staying within the weight limit.
Q5- In the Fractional Knapsack Algorithm, items are sorted based on what criteria?
1. Item value
2. Item weight-to-value ratio
3. Item value-to-weight ratio
4. Item size
Ans – (3)
Explanation – Items are sorted in non-ascending order of their value-to-weight ratios to select the most valuable items first.
Q6- When does the Fractional Knapsack Algorithm break down, and dynamic programming is preferred?
1. When items cannot be divided into fractions
2. When there are only a few items
3. When the knapsack has a small capacity
4. When items have equal values
Ans – (1)
Explanation – Dynamic programming is preferred when items cannot be divided into fractions, and a more comprehensive approach is needed.
Q7- Fractional knapsack problem is also known as __________
1. 0/1 knapsack problem
2. Continuous knapsack problem
3. Divisible knapsack problem
4. Non continuous knapsack problem
Ans – (2)
Explanation – The weight is fully occupied by the items because the items are divisible in the fractional knapsack problem. That’s why it is called Continuous knapsack problem.
It does not pronounce divisible knapsack problem.
Q8- Fractional knapsack problem can be solved in time O(n).
1. True
2. False
Ans – (1)
Explanation – It is possible to solve the problem in O(n) time by adapting the algorithm for finding weighted medians.
Q9- Given items as {value, weight} pairs {{40, 20}, {30, 10}, {20, 5}}. The capacity of knapsack=20. Find the maximum value output assuming items to be divisible.
1. 60
2. 80
3. 100
4. 40
Ans – (1)
Explanation –
{value, weight, value/weight ratio}
{40, 20, 2},
{30, 10, 3},
{20, 5, 4}}
So, we include the second and third items wholly into the knapsack. This leaves only 5 units of volume for the first item. So, we include the first item partially.
Final value profit = 20 + 30 + 40 x (5/20) = 60.
Q10- Given items as {value, weight} pairs {{60, 20}, {50, 25}, {20, 5}}. The capacity of knapsack=40. Find the maximum value output assuming items to be divisible and non-divisible respectively.
1. 100, 80
2. 110, 70
3. 130, 110
4. 110, 80
Ans – (4)
Explanation –
Assuming items to be divisible
{value, weight, value/weight ratio}
{60, 20, 3},
{50, 25, 2},
{20, 5, 4}}
As a result, we include the third and first things entirely. Knapsack capacity = 40 – 5 – 20 = 15
So, now only 15 units of volume are left for second item. So, we include it partially.
Final value profit = 20 + 60 + 50 x (15/25) = 80 + 30 = 110
Assuming items to be indivisible
In this case we will have to leave one item due to insufficient capacity.
Final volume = 60 + 20 = 80.
Q11- The result of the fractional knapsack is greater than or equal to 0/1 knapsack.
1. True
2. False
Ans – (1)
Explanation – As fractional knapsack gives extra liberty to include the object partially which is not possible with 0/1 knapsack, thus we get better results with a fractional knapsack.






